12.1 全等三角形同步练习(含解析)
文档属性
| 名称 | 12.1 全等三角形同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1009.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:30:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上
12.1全等三角形同步练习
一.选择题
1.(2020秋?抚顺县期末)下列各组中的两个图形属于全等图形的是( )
A.
B.C.
D.
2.(2021春?峄城区期末)如图,点E,F是线段BC上的两点,如果△ABF≌△DCE,AB=3,则DC的长等于( )
A.3
B.4
C.5
D.6
3.(2021春?庐山市
期末)如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
4.(2021春?宽城区期末)如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED
B.∠BAD=∠CAE
C.AB=AE
D.AC=DE
5.(2021春?万州区期末)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°.则∠DFA的度数为( )
A.65°
B.70°
C.85°
D.110°
6.(2021春?城固县期末)如图,已知△OAB≌△OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是( )
A.∠BDO=62°
B.∠BOC=21°
C.OC=4
D.CD∥OA
7.(2021春?平顶山期末)如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34°
B.40°
C.45°
D.60°
8.(2021春?商水县期末)下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
9.(2021?哈尔滨)如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30°
B.25°
C.35°
D.65°
10.(2021春?泰兴市期末)边长都为整数的△ABC和△DEF全等,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为奇数,则DF的值为( )
A.3
B.4
C.3或5
D.3或4或5
二.填空题
11.(2020秋?云南期末)已知△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC=
.
12.(2020秋?秦淮区期中)已知△ABC≌△DEF,BC=EF=10cm,若△DEF的面积是40cm2,则△ABC中BC边上的高是
cm.
13.(2020春?河南期末)如图,已知△ABC≌△ADE,若∠A=60°,∠B=40°,则∠BED的大小为
.
14.(2021春?叙州区期末)如图,△ABC≌△ADE,且∠EAB=112°,则∠EFC=
度.
15.(2020秋?姜堰区期末)一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=
.
16.(2021春?莱州市期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于
.
三.解答题
17.(2019秋?内乡县期末)如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
18.(2021春?宝安区期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
19.(2021春?二道区期末)如图,△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,点C为AD中点.
(1)求∠BAE的度数和AE的长.
(2)延长BC交ED于点F,则∠DFC的大小为
度.
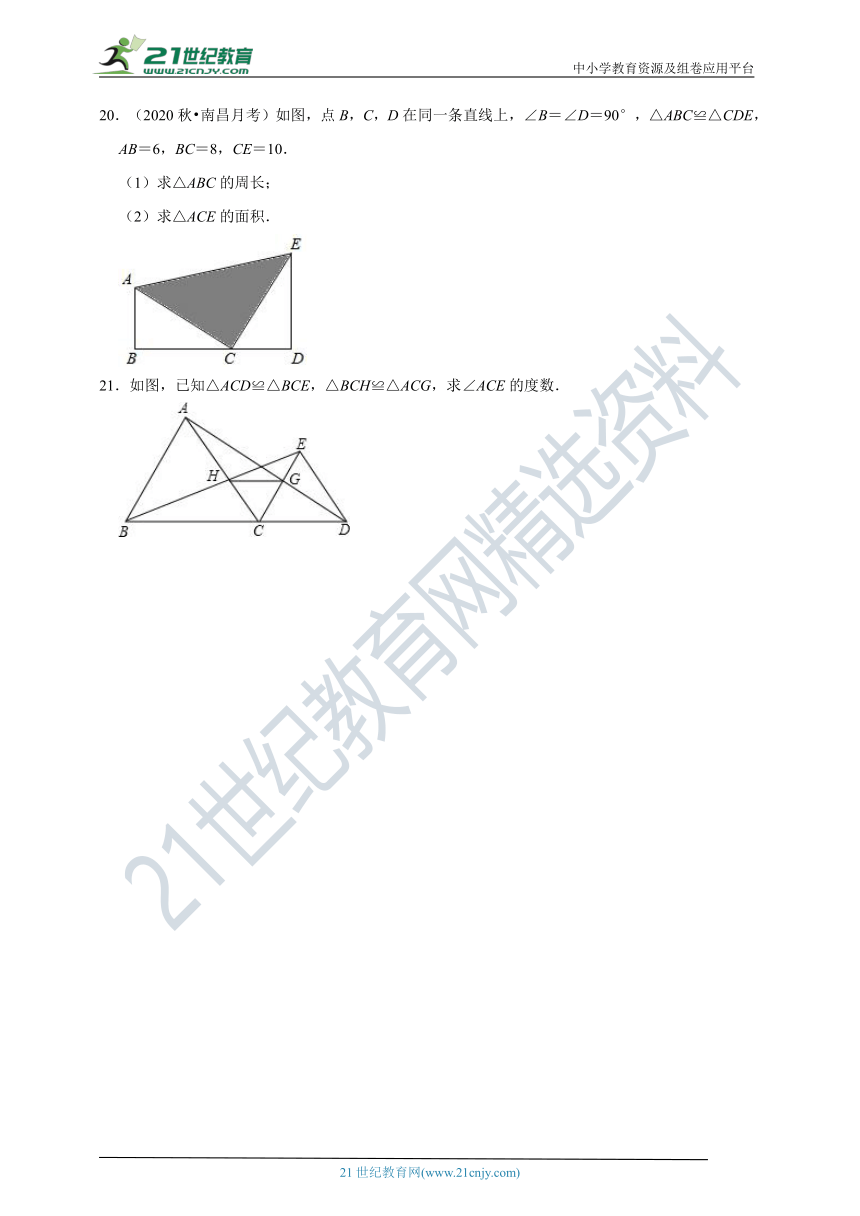
20.(2020秋?南昌月考)如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.
(1)求△ABC的周长;
(2)求△ACE的面积.
21.如图,已知△ACD≌△BCE,△BCH≌△ACG,求∠ACE的度数.
答案与解析
一.选择题
1.(2020秋?抚顺县期末)下列各组中的两个图形属于全等图形的是( )
A.B.
C.
D.
【解析】解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误;
故选:B.
2.(2021春?峄城区期末)如图,点E,F是线段BC上的两点,如果△ABF≌△DCE,AB=3,则DC的长等于( )
A.3
B.4
C.5
D.6
【解析】解:∵△ABF≌△DCE,AB=3,
∴CD=AB=3,
故选:A.
3.(2021春?庐山市
期末)如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
【解析】解:∵△ABE≌△ACD,∠C=30°,
∴∠B=∠C=30°,
∵∠BDM是△ADC的外角,
∴∠BDM=∠A+∠C=100°,
∴∠BMD=180°﹣∠BDM﹣∠B=180°﹣100°﹣30°=50°,
故选:A.
4.(2021春?宽城区期末)如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED
B.∠BAD=∠CAE
C.AB=AE
D.AC=DE
【解析】解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
5.(2021春?万州区期末)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°.则∠DFA的度数为( )
A.65°
B.70°
C.85°
D.110°
【解析】解:∵△ABC≌△DEC,∠B=∠CEB=65°,
∴∠DEC=∠B=65°,
∴∠AEF=180°﹣65°﹣65°=50°,
∴∠DFA=∠A+∠AEF=20°+50°=70°,
故选:B.
6.(2021春?城固县期末)如图,已知△OAB≌△OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是( )
A.∠BDO=62°
B.∠BOC=21°
C.OC=4
D.CD∥OA
【解析】解:A、∵△OAB≌△OCD,
∴OA=OC,OB=OD,∠COD=∠AOB,
∴∠OAC=∠OCA=62°,∠OBD=∠ODB,∠BOD=∠AOC,
∴∠AOC=180°﹣∠OAC﹣∠OCA=56°,
∴∠BOD=∠AOC=56°,
∴∠BDO=×(180°﹣56°)=62°,故本选项说法正确,不符合题意;
B、∵∠AOC=56°,∠AOB=35°,
∴∠BOC=56°﹣35°=21°,故本选项说法正确,不符合题意;
C、∵△OAB≌△OCD,OA=4,
∴OC=OA=4,故本选项说法正确,不符合题意;
D、∵∠AOC=56°,∠OCD不一定是56°,
∴CD与OA不一定平行,故本选项说法错误,符合题意;
故选:D.
7.(2021春?平顶山期末)如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34°
B.40°
C.45°
D.60°
【解析】解:∵∠CDB′=94°,
∴∠ADB=∠CDB′=94°,
∴∠BAD=180°﹣∠B﹣∠ADB=60°,
∵AB′平分∠BAC,
∴∠BAC=2∠BAD=120°,
∴∠C=180°﹣∠B﹣∠BAC=34°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=34°,
故选:A.
8.(2021春?商水县期末)下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
【解析】解:A、如果两个图形全等,那么它们的形状和大小一定相同,正确,不合题意;
B、面积相等的两个图形是全等图形,错误,符合题意;
C、图形全等,只与形状、大小有关,而与它们的位置无关,正确,不合题意;
D、全等三角形的对应边相等,对应角相等,正确,不合题意;
故选:B.
9.(2021?哈尔滨)如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30°
B.25°
C.35°
D.65°
【解析】解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
10.(2021春?泰兴市期末)边长都为整数的△ABC和△DEF全等,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为奇数,则DF的值为( )
A.3
B.4
C.3或5
D.3或4或5
【解析】解:AC的范围是2<AC<6,则AC的奇数值是3或5.
△ABC和△DEF全等,AB与DE是对应边,则DE=AB=2,
当DF=AC时,DF=3或5.
当DF=BC时,DF=4.
故选:D.
二.填空题
11.(2020秋?云南期末)已知△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC= 5 .
【解析】解:∵△ABC≌△DEF,
∴EF=BC=4,
在△ABC中,△ABC的周长为12,AB=3,
∴AC=12﹣AB﹣BC=12﹣4﹣3=5,
故填5.
12.(2020秋?秦淮区期中)已知△ABC≌△DEF,BC=EF=10cm,若△DEF的面积是40cm2,则△ABC中BC边上的高是 8 cm.
【解析】解:设△DEF中BC边上的高是hcm,
由题意得,×10×h=40,
解得,h=8,
∵△ABC≌△DEF,
∴△ABC中BC边上的高=△DEF中BC边上的高=8cm,
故答案为:8.
13.(2020春?河南期末)如图,已知△ABC≌△ADE,若∠A=60°,∠B=40°,则∠BED的大小为 100° .
【解析】解:∵△ABC≌△ADE,
∴∠D=∠B=40°,
∴∠BED=∠A+∠D=60°+40°=100°,
故答案为:100°.
14.(2021春?叙州区期末)如图,△ABC≌△ADE,且∠EAB=112°,则∠EFC= 124 度.
【解析】解:∵△ABC≌△ADE,∠EAB=112°,
∴∠EAD=DAB=56°,∠D=∠B,
∴∠ACB+∠B=180°﹣56°=124°,
∵∠ACB=∠FCD,
∴∠FCD+∠D=124°,
∵∠EFC是△FCD的一个外角,
∴∠EFC=∠FCD+∠D=124°,
故答案为:124.
15.(2020秋?姜堰区期末)一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= 11 .
【解析】解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
16.(2021春?莱州市期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于
180° .
【解析】解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个三角形全等,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
故答案为:180°.
三.解答题
17.(2019秋?内乡县期末)如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
【解析】解:(1)∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠DCF+∠D=70°;
(2)∵△ABF≌△CDE,
∴BF=DE,
∴BF﹣EF=DE﹣EF,即BE=DF,
∵BD=10,EF=2,
∴BE=(10﹣2)÷2=4,
∴BF=BE+EF=6.
18.(2021春?宝安区期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
【解析】(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
19.(2021春?二道区期末)如图,△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,点C为AD中点.
(1)求∠BAE的度数和AE的长.
(2)延长BC交ED于点F,则∠DFC的大小为
150 度.
【解析】解:(1)∵△ABC≌△ADE,∠B=10°,AB=4cm,
∴∠ADE=∠B=10°,∠EAD=∠CAB,AD=AB=4cm,
∵∠AED=20°,
∴∠EAD=180°﹣∠EAD﹣∠AED=180°﹣10°﹣20°=150°,
∴∠CAB=150°,
∴∠EAB=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC=AD=×4=2(cm),
∴AE=2cm;
(2)∵∠B=10°,∠CAB=150°,
∴∠ACB=180°﹣150°﹣10°=20°,
∴∠FCD=20°,
∴∠DFC=180°﹣20°﹣10°=150°,
故答案为:150.
20.(2020秋?南昌月考)如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.
(1)求△ABC的周长;
(2)求△ACE的面积.
【解析】解:(1)∵△ABC≌△CDE,CE=10,
∴AC=CE=10,
∵AB=6,BC=8,
∴△ABC的周长=AB+BC+AC=6+8+10=24;
(2)∵∠B=90°,
∴∠ACB+∠BAC=90°,
∵△ABC≌△CDE,
∴∠ECD=∠CAB,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°,
∵AC=CE=10,
∴△ACE的面积=×10×10=50.
21.如图,已知△ACD≌△BCE,△BCH≌△ACG,求∠ACE的度数.
【解析】解:∵△ACD≌△BCE,△BCH≌△ACG,
∴∠ACE=∠BCH,∠ACD=∠BCE,
∴∠ACD﹣∠ACE=∠BCE﹣∠BCH,
∴∠DCG=∠ACG,
即∠BCA=∠ACE=∠DCE,
∵∠BCA+∠ACE+∠DCE=180°,
∴∠ACE=∠ACE=∠DCE=60°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上
12.1全等三角形同步练习
一.选择题
1.(2020秋?抚顺县期末)下列各组中的两个图形属于全等图形的是( )
A.
B.C.
D.
2.(2021春?峄城区期末)如图,点E,F是线段BC上的两点,如果△ABF≌△DCE,AB=3,则DC的长等于( )
A.3
B.4
C.5
D.6
3.(2021春?庐山市
期末)如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
4.(2021春?宽城区期末)如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED
B.∠BAD=∠CAE
C.AB=AE
D.AC=DE
5.(2021春?万州区期末)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°.则∠DFA的度数为( )
A.65°
B.70°
C.85°
D.110°
6.(2021春?城固县期末)如图,已知△OAB≌△OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是( )
A.∠BDO=62°
B.∠BOC=21°
C.OC=4
D.CD∥OA
7.(2021春?平顶山期末)如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34°
B.40°
C.45°
D.60°
8.(2021春?商水县期末)下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
9.(2021?哈尔滨)如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30°
B.25°
C.35°
D.65°
10.(2021春?泰兴市期末)边长都为整数的△ABC和△DEF全等,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为奇数,则DF的值为( )
A.3
B.4
C.3或5
D.3或4或5
二.填空题
11.(2020秋?云南期末)已知△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC=
.
12.(2020秋?秦淮区期中)已知△ABC≌△DEF,BC=EF=10cm,若△DEF的面积是40cm2,则△ABC中BC边上的高是
cm.
13.(2020春?河南期末)如图,已知△ABC≌△ADE,若∠A=60°,∠B=40°,则∠BED的大小为
.
14.(2021春?叙州区期末)如图,△ABC≌△ADE,且∠EAB=112°,则∠EFC=
度.
15.(2020秋?姜堰区期末)一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=
.
16.(2021春?莱州市期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于
.
三.解答题
17.(2019秋?内乡县期末)如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
18.(2021春?宝安区期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
19.(2021春?二道区期末)如图,△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,点C为AD中点.
(1)求∠BAE的度数和AE的长.
(2)延长BC交ED于点F,则∠DFC的大小为
度.
20.(2020秋?南昌月考)如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.
(1)求△ABC的周长;
(2)求△ACE的面积.
21.如图,已知△ACD≌△BCE,△BCH≌△ACG,求∠ACE的度数.
答案与解析
一.选择题
1.(2020秋?抚顺县期末)下列各组中的两个图形属于全等图形的是( )
A.B.
C.
D.
【解析】解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能够完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误;
故选:B.
2.(2021春?峄城区期末)如图,点E,F是线段BC上的两点,如果△ABF≌△DCE,AB=3,则DC的长等于( )
A.3
B.4
C.5
D.6
【解析】解:∵△ABF≌△DCE,AB=3,
∴CD=AB=3,
故选:A.
3.(2021春?庐山市
期末)如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50°
B.65°
C.70°
D.80°
【解析】解:∵△ABE≌△ACD,∠C=30°,
∴∠B=∠C=30°,
∵∠BDM是△ADC的外角,
∴∠BDM=∠A+∠C=100°,
∴∠BMD=180°﹣∠BDM﹣∠B=180°﹣100°﹣30°=50°,
故选:A.
4.(2021春?宽城区期末)如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED
B.∠BAD=∠CAE
C.AB=AE
D.AC=DE
【解析】解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
5.(2021春?万州区期末)如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°.则∠DFA的度数为( )
A.65°
B.70°
C.85°
D.110°
【解析】解:∵△ABC≌△DEC,∠B=∠CEB=65°,
∴∠DEC=∠B=65°,
∴∠AEF=180°﹣65°﹣65°=50°,
∴∠DFA=∠A+∠AEF=20°+50°=70°,
故选:B.
6.(2021春?城固县期末)如图,已知△OAB≌△OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是( )
A.∠BDO=62°
B.∠BOC=21°
C.OC=4
D.CD∥OA
【解析】解:A、∵△OAB≌△OCD,
∴OA=OC,OB=OD,∠COD=∠AOB,
∴∠OAC=∠OCA=62°,∠OBD=∠ODB,∠BOD=∠AOC,
∴∠AOC=180°﹣∠OAC﹣∠OCA=56°,
∴∠BOD=∠AOC=56°,
∴∠BDO=×(180°﹣56°)=62°,故本选项说法正确,不符合题意;
B、∵∠AOC=56°,∠AOB=35°,
∴∠BOC=56°﹣35°=21°,故本选项说法正确,不符合题意;
C、∵△OAB≌△OCD,OA=4,
∴OC=OA=4,故本选项说法正确,不符合题意;
D、∵∠AOC=56°,∠OCD不一定是56°,
∴CD与OA不一定平行,故本选项说法错误,符合题意;
故选:D.
7.(2021春?平顶山期末)如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34°
B.40°
C.45°
D.60°
【解析】解:∵∠CDB′=94°,
∴∠ADB=∠CDB′=94°,
∴∠BAD=180°﹣∠B﹣∠ADB=60°,
∵AB′平分∠BAC,
∴∠BAC=2∠BAD=120°,
∴∠C=180°﹣∠B﹣∠BAC=34°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=34°,
故选:A.
8.(2021春?商水县期末)下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
【解析】解:A、如果两个图形全等,那么它们的形状和大小一定相同,正确,不合题意;
B、面积相等的两个图形是全等图形,错误,符合题意;
C、图形全等,只与形状、大小有关,而与它们的位置无关,正确,不合题意;
D、全等三角形的对应边相等,对应角相等,正确,不合题意;
故选:B.
9.(2021?哈尔滨)如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30°
B.25°
C.35°
D.65°
【解析】解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
10.(2021春?泰兴市期末)边长都为整数的△ABC和△DEF全等,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为奇数,则DF的值为( )
A.3
B.4
C.3或5
D.3或4或5
【解析】解:AC的范围是2<AC<6,则AC的奇数值是3或5.
△ABC和△DEF全等,AB与DE是对应边,则DE=AB=2,
当DF=AC时,DF=3或5.
当DF=BC时,DF=4.
故选:D.
二.填空题
11.(2020秋?云南期末)已知△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC= 5 .
【解析】解:∵△ABC≌△DEF,
∴EF=BC=4,
在△ABC中,△ABC的周长为12,AB=3,
∴AC=12﹣AB﹣BC=12﹣4﹣3=5,
故填5.
12.(2020秋?秦淮区期中)已知△ABC≌△DEF,BC=EF=10cm,若△DEF的面积是40cm2,则△ABC中BC边上的高是 8 cm.
【解析】解:设△DEF中BC边上的高是hcm,
由题意得,×10×h=40,
解得,h=8,
∵△ABC≌△DEF,
∴△ABC中BC边上的高=△DEF中BC边上的高=8cm,
故答案为:8.
13.(2020春?河南期末)如图,已知△ABC≌△ADE,若∠A=60°,∠B=40°,则∠BED的大小为 100° .
【解析】解:∵△ABC≌△ADE,
∴∠D=∠B=40°,
∴∠BED=∠A+∠D=60°+40°=100°,
故答案为:100°.
14.(2021春?叙州区期末)如图,△ABC≌△ADE,且∠EAB=112°,则∠EFC= 124 度.
【解析】解:∵△ABC≌△ADE,∠EAB=112°,
∴∠EAD=DAB=56°,∠D=∠B,
∴∠ACB+∠B=180°﹣56°=124°,
∵∠ACB=∠FCD,
∴∠FCD+∠D=124°,
∵∠EFC是△FCD的一个外角,
∴∠EFC=∠FCD+∠D=124°,
故答案为:124.
15.(2020秋?姜堰区期末)一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= 11 .
【解析】解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
16.(2021春?莱州市期末)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于
180° .
【解析】解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个三角形全等,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
故答案为:180°.
三.解答题
17.(2019秋?内乡县期末)如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
【解析】解:(1)∵△ABF≌△CDE,
∴∠D=∠B=30°,
∴∠EFC=∠DCF+∠D=70°;
(2)∵△ABF≌△CDE,
∴BF=DE,
∴BF﹣EF=DE﹣EF,即BE=DF,
∵BD=10,EF=2,
∴BE=(10﹣2)÷2=4,
∴BF=BE+EF=6.
18.(2021春?宝安区期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
【解析】(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
19.(2021春?二道区期末)如图,△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,点C为AD中点.
(1)求∠BAE的度数和AE的长.
(2)延长BC交ED于点F,则∠DFC的大小为
150 度.
【解析】解:(1)∵△ABC≌△ADE,∠B=10°,AB=4cm,
∴∠ADE=∠B=10°,∠EAD=∠CAB,AD=AB=4cm,
∵∠AED=20°,
∴∠EAD=180°﹣∠EAD﹣∠AED=180°﹣10°﹣20°=150°,
∴∠CAB=150°,
∴∠EAB=360°﹣150°﹣150°=60°,
∵点C为AD中点,
∴AC=AD=×4=2(cm),
∴AE=2cm;
(2)∵∠B=10°,∠CAB=150°,
∴∠ACB=180°﹣150°﹣10°=20°,
∴∠FCD=20°,
∴∠DFC=180°﹣20°﹣10°=150°,
故答案为:150.
20.(2020秋?南昌月考)如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.
(1)求△ABC的周长;
(2)求△ACE的面积.
【解析】解:(1)∵△ABC≌△CDE,CE=10,
∴AC=CE=10,
∵AB=6,BC=8,
∴△ABC的周长=AB+BC+AC=6+8+10=24;
(2)∵∠B=90°,
∴∠ACB+∠BAC=90°,
∵△ABC≌△CDE,
∴∠ECD=∠CAB,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°,
∵AC=CE=10,
∴△ACE的面积=×10×10=50.
21.如图,已知△ACD≌△BCE,△BCH≌△ACG,求∠ACE的度数.
【解析】解:∵△ACD≌△BCE,△BCH≌△ACG,
∴∠ACE=∠BCH,∠ACD=∠BCE,
∴∠ACD﹣∠ACE=∠BCE﹣∠BCH,
∴∠DCG=∠ACG,
即∠BCA=∠ACE=∠DCE,
∵∠BCA+∠ACE+∠DCE=180°,
∴∠ACE=∠ACE=∠DCE=60°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
