13.2 画轴对称图形同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级上
13.2画轴对称图形同步练习
一.选择题
1.(2021春?长春期末)在平面直角坐标系中,若点A(2,a)和B(2,7)关于x轴对称,则a的值为( )
A.2
B.﹣2
C.7
D.﹣7
2.(2021春?道县期末)如果点P(m,﹣2,)和点Q(﹣3,n)关于x轴对称,则m+n的值是( )
A.﹣1
B.1
C.﹣5
D.5
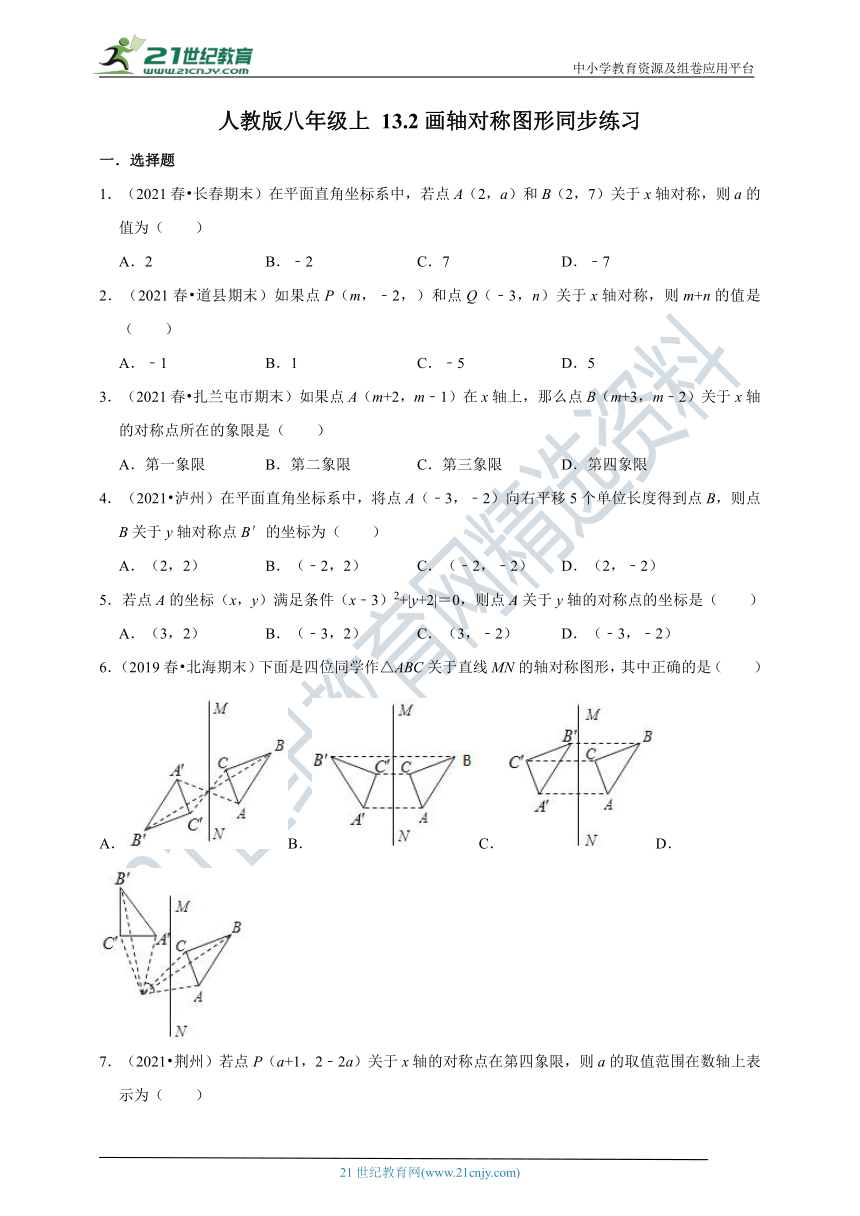
3.(2021春?扎兰屯市期末)如果点A(m+2,m﹣1)在x轴上,那么点B(m+3,m﹣2)关于x轴的对称点所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.(2021?泸州)在平面直角坐标系中,将点A(﹣3,﹣2)向右平移5个单位长度得到点B,则点B关于y轴对称点B′的坐标为( )
A.(2,2)
B.(﹣2,2)
C.(﹣2,﹣2)
D.(2,﹣2)
5.若点A的坐标(x,y)满足条件(x﹣3)2+|y+2|=0,则点A关于y轴的对称点的坐标是( )
A.(3,2)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣3,﹣2)
6.(2019春?北海期末)下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A.B.C.D.
7.(2021?荆州)若点P(a+1,2﹣2a)关于x轴的对称点在第四象限,则a的取值范围在数轴上表示为( )
A.
B.
C.
D.
8.若点P(m2﹣2,m)在第一象限的角平分线上,则点(|m|,m﹣1)关于y轴的对称点的坐标是( )
A.(2,)
B.(1,﹣1)
C.(﹣2,)
D.(﹣1,﹣1)
9.(2020秋?太原期末)已知点P(2,﹣4)与点Q(6,﹣4)关于某条直线对称,则这条直线是( )
A.x轴
B.y轴
C.过点(4,0)且垂直于x轴的直线
D.过点(0,﹣4)且平行于x轴的直线
10.下列关于A,B两点的说法中,正确的个数是( )
①如果点A与点B关于y轴对称,则它们的纵坐标相同
②如果点A与点B的纵坐标相同,则它们关于y轴对称
③如果点A与点B的横坐标相同,则它们关于x轴对称
④如果点A与点B关于x轴对称,则它们的横坐标相同
A.1个
B.2个
C.3个
D.4个
二.填空题
11.(2020秋?余干县期中)在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点P',则点P'关于x轴的对称点的坐标为
.
12.(2020秋?吉林期末)在平面直角坐标系中,已知点A的坐标为(﹣2,5),点Q与点A关于y轴对称,点P与点Q关于x轴对称,则点P的坐标是
.
13.(2021春?东湖区期末)点P(m+2,n)向右平移两个单位后得到的点和点Q(n﹣1,2m+1)关于y轴对称,则m+n=
.
14.(2021?天宁区校级模拟)在平面直角坐标系中,若点M(2a+7,0)和N(2﹣b,a+b)关于y轴对称,则ab=
.
15.(2020?海淀区二模)如图,在平面直角坐标系xOy中,已知点C(3,2),将△ABC关于直线x=4对称,得到△A1B1C1,则点C的对应点C1的坐标为
;再将△A1B1C1向上平移一个单位长度,得到△A2B2C2,则点C1的对应点C2的坐标为
.
16.(2018秋?南岸区期末)如图,在平面直角坐标系中,将△ABC三个顶点的横坐标分别乘以﹣1,而纵坐标保持不变,得到△A′B′C′,则△A′B′C′和△ABC关于
对称(横线上填“x轴”、“y轴”或“原点”).
三.解答题
17.(2021春?榆阳区期末)如图,在边长为1的正方形网格中,△ABC的三个顶点都在格点上,在图中画出△ABC关于直线l对称的△A'B'C'.
18.(2021春?射阳县校级期末)如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于直线m对称的△A2B2C2;
(3)△ABC的面积为
.
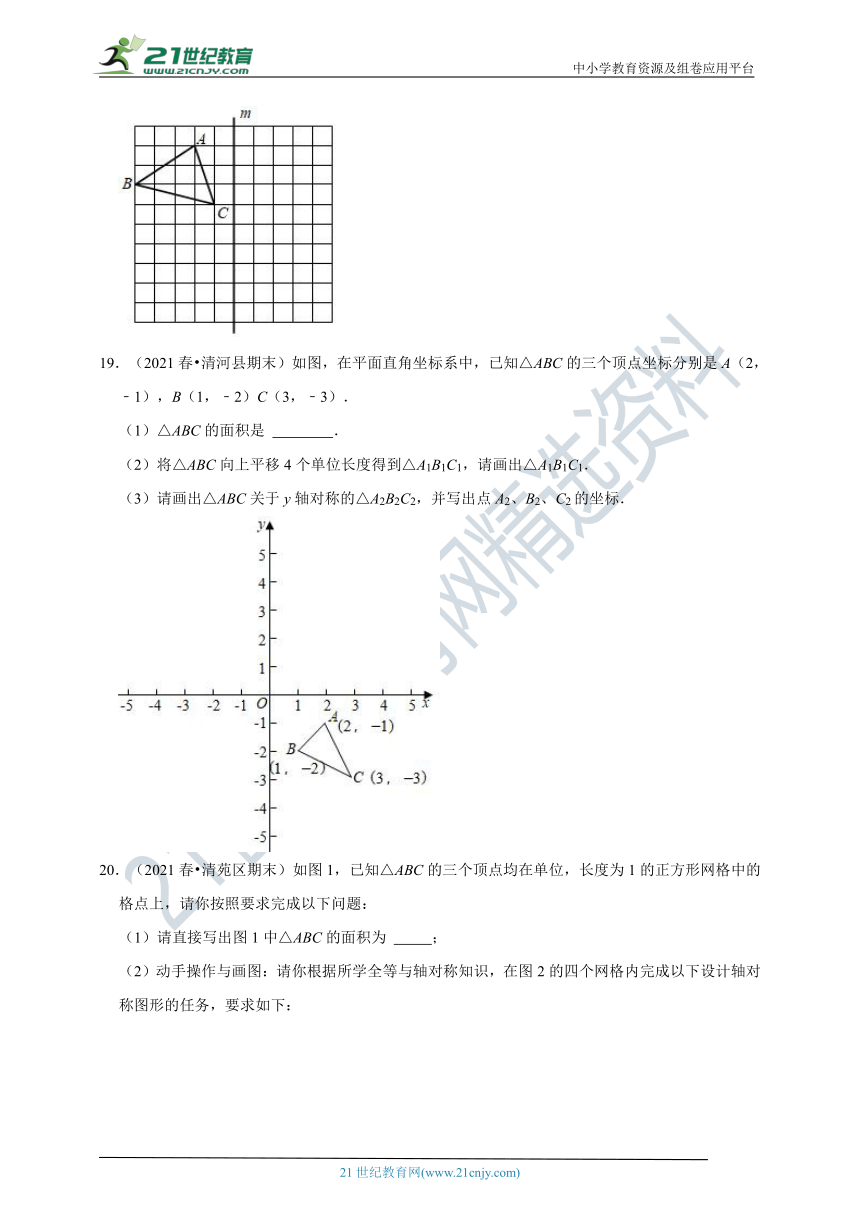
19.(2021春?清河县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2)C(3,﹣3).
(1)△ABC的面积是
.
(2)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1.
(3)请画出△ABC关于y轴对称的△A2B2C2,并写出点A2、B2、C2的坐标.
20.(2021春?清苑区期末)如图1,已知△ABC的三个顶点均在单位,长度为1的正方形网格中的格点上,请你按照要求完成以下问题:
(1)请直接写出图1中△ABC的面积为
;
(2)动手操作与画图:请你根据所学全等与轴对称知识,在图2的四个网格内完成以下设计轴对称图形的任务,要求如下:
①画出的三角形要与△ABC全等,且它们的顶点都在格点上;
②画出的三角形与△ABC关于某条直线成轴对称图形.
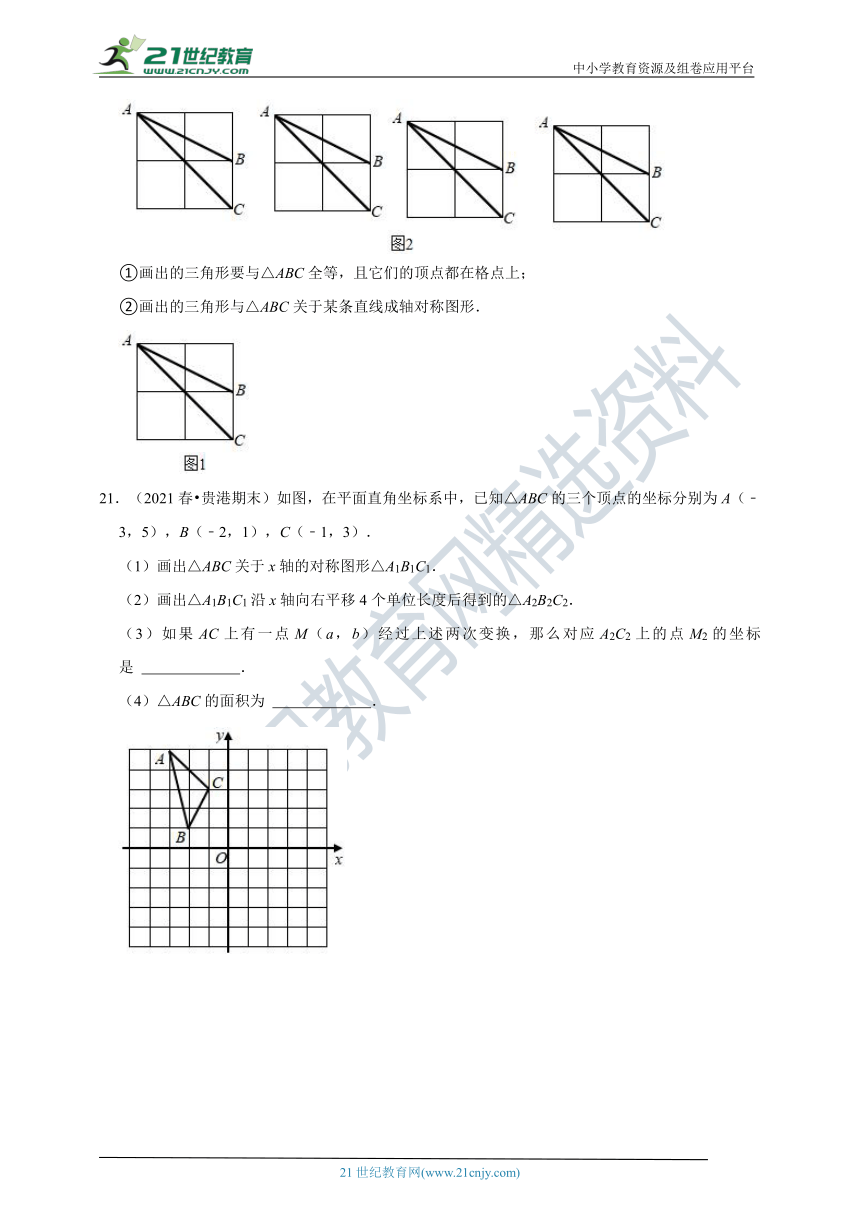
21.(2021春?贵港期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1.
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2.
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是
.
(4)△ABC的面积为
.
答案与解析
一.选择题
1.(2021春?长春期末)在平面直角坐标系中,若点A(2,a)和B(2,7)关于x轴对称,则a的值为( )
A.2
B.﹣2
C.7
D.﹣7
【解析】解:∵点A(2,a)和B(2,7)关于x轴对称,
∴a=﹣7.
故选:D.
2.(2021春?道县期末)如果点P(m,﹣2,)和点Q(﹣3,n)关于x轴对称,则m+n的值是( )
A.﹣1
B.1
C.﹣5
D.5
【解析】解:∵点P(m,﹣2,)和点Q(﹣3,n)关于x轴对称,
∴m=﹣3,n=2,
则m+n=﹣3+2=﹣1.
故选:A.
3.(2021春?扎兰屯市期末)如果点A(m+2,m﹣1)在x轴上,那么点B(m+3,m﹣2)关于x轴的对称点所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【解析】解:∵点A(m+2,m﹣1)在x轴上,
∴m﹣1=0,
即m=1,
∴m+3=4,m﹣2=﹣1,
∴点B(4,﹣1),
∴点B(4,﹣1)在第四象限,
∴点B(4,﹣1)关于x轴的对称点在第一象限,
故选:A.
4.(2021?泸州)在平面直角坐标系中,将点A(﹣3,﹣2)向右平移5个单位长度得到点B,则点B关于y轴对称点B′的坐标为( )
A.(2,2)
B.(﹣2,2)
C.(﹣2,﹣2)
D.(2,﹣2)
【解析】解:点A(﹣3,﹣2)向右平移5个单位长度得到的B的坐标为(﹣3+5,﹣2),即(2,﹣2),
则点B关于y轴的对称点B′的坐标是:(﹣2,﹣2).
故选:C.
5.若点A的坐标(x,y)满足条件(x﹣3)2+|y+2|=0,则点A关于y轴的对称点的坐标是( )
A.(3,2)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣3,﹣2)
【解析】解:由点A的坐标(x,y)满足条件(x﹣3)2+|y+2|=0,得
x﹣3=0,y+2=0.
解得x=3,y=﹣2.即A(3,﹣2).
点A关于y轴的对称点的坐标是(﹣3,﹣2),
故选:D.
6.(2019春?北海期末)下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A.B.C.D.
【解析】解:作△ABC关于直线MN的轴对称图形正确的是B选项,
故选:B.
7.(2021?荆州)若点P(a+1,2﹣2a)关于x轴的对称点在第四象限,则a的取值范围在数轴上表示为( )
A.
B.
C.
D.
【解析】解:∵点P(a+1,2﹣2a)关于x轴的对称点在第四象限,
∴点P在第一象限,
∴,
解得:﹣1<a<1,
在数轴上表示为:,
故选:C.
8.若点P(m2﹣2,m)在第一象限的角平分线上,则点(|m|,m﹣1)关于y轴的对称点的坐标是( )
A.(2,)
B.(1,﹣1)
C.(﹣2,)
D.(﹣1,﹣1)
【解析】解:∵若点P(m2﹣2,m)在第一象限的角平分线上,
∴m2﹣2=m,m>0,
解得:m=2,
∴点(|m|,m﹣1)就是(2,),
∴关于y轴的对称点的坐标是(﹣2,),
故选:C.
9.(2020秋?太原期末)已知点P(2,﹣4)与点Q(6,﹣4)关于某条直线对称,则这条直线是( )
A.x轴
B.y轴
C.过点(4,0)且垂直于x轴的直线
D.过点(0,﹣4)且平行于x轴的直线
【解析】解:点P(2,﹣4)与点Q(6,﹣4)的位置关系是关于直线x=4对称,
故选:C.
10.下列关于A,B两点的说法中,正确的个数是( )
①如果点A与点B关于y轴对称,则它们的纵坐标相同
②如果点A与点B的纵坐标相同,则它们关于y轴对称
③如果点A与点B的横坐标相同,则它们关于x轴对称
④如果点A与点B关于x轴对称,则它们的横坐标相同
A.1个
B.2个
C.3个
D.4个
【解析】解:正确的是:①如果点A与点B关于y轴对称,则它们的纵坐标相同;
④如果点A与点B关于x轴对称,则它们的横坐标相同;
故正确的有两个;
故选:B.
二.填空题
11.(2020秋?余干县期中)在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点P',则点P'关于x轴的对称点的坐标为 (0,﹣2) .
【解析】解:∵将点P(﹣3,2)向右平移3个单位得到点P',
∴点P'坐标为:(0,2),
∴点P'关于x轴的对称点的坐标为(0,﹣2).
故答案为:(0,﹣2).
12.(2020秋?吉林期末)在平面直角坐标系中,已知点A的坐标为(﹣2,5),点Q与点A关于y轴对称,点P与点Q关于x轴对称,则点P的坐标是 (2,﹣5) .
【解析】解:∵点A的坐标为(﹣2,5),点Q与点A关于y轴对称,
∴点Q的坐标为(2,5),
∵点P与点Q关于x轴对称,
∴点P的坐标是(2,﹣5).
故答案为:(2,﹣5).
13.(2021春?东湖区期末)点P(m+2,n)向右平移两个单位后得到的点和点Q(n﹣1,2m+1)关于y轴对称,则m+n= ﹣3 .
【解析】解:点P(m+2,n)向右平移两个单位后得到(m+4,n),
∵点P(m+2,n)向右平移两个单位后得到的点(m+4,n)和点Q(n﹣1,2m+1)关于y轴对称,
∴,
解得:,
故m+n=﹣﹣=﹣3.
故答案为:﹣3.
14.(2021?天宁区校级模拟)在平面直角坐标系中,若点M(2a+7,0)和N(2﹣b,a+b)关于y轴对称,则ab= ﹣27 .
【解析】解:∵点M(2a+7,0)和N(2﹣b,a+b)关于y轴对称,
∴,
解得:,
则ab=(﹣3)3=﹣27.
故答案为:﹣27.
15.(2020?海淀区二模)如图,在平面直角坐标系xOy中,已知点C(3,2),将△ABC关于直线x=4对称,得到△A1B1C1,则点C的对应点C1的坐标为 (5,2) ;再将△A1B1C1向上平移一个单位长度,得到△A2B2C2,则点C1的对应点C2的坐标为 (5,3) .
【解析】解:如图△A1B1C1,△A2B2C2,即为所求.C1(5,2),C2(5,3).
故答案为(5,2),(5,3).
16.(2018秋?南岸区期末)如图,在平面直角坐标系中,将△ABC三个顶点的横坐标分别乘以﹣1,而纵坐标保持不变,得到△A′B′C′,则△A′B′C′和△ABC关于 y轴 对称(横线上填“x轴”、“y轴”或“原点”).
【解析】解:∵横坐标乘以﹣1,
∴横坐标相反,又纵坐标不变,
∴关于y轴对称.
故答案为:y轴.
三.解答题
17.(2021春?榆阳区期末)如图,在边长为1的正方形网格中,△ABC的三个顶点都在格点上,在图中画出△ABC关于直线l对称的△A'B'C'.
【解析】解:如图,△A′B′C′即为所求.
18.(2021春?射阳县校级期末)如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于直线m对称的△A2B2C2;
(3)△ABC的面积为
5.5 .
【解析】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)△ABC的面积=4×3﹣×1×3﹣×4×1﹣×2×3=5.5.
故答案为5.5.
19.(2021春?清河县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2)C(3,﹣3).
(1)△ABC的面积是
3.5 .
(2)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1.
(3)请画出△ABC关于y轴对称的△A2B2C2,并写出点A2、B2、C2的坐标.
【解析】解:(1)根据A(2,﹣1),B(1,﹣2)C(3,﹣3).
∴△ABC的面积=2×2﹣1×11×21×2=1.5;
故答案为:1.5;
(2)如图,△A1B1C1即为所求;
(3)△A2B2C2即为所求;A2(﹣2,﹣1),B2(﹣1,﹣2),C2(﹣3,﹣3).
20.(2021春?清苑区期末)如图1,已知△ABC的三个顶点均在单位,长度为1的正方形网格中的格点上,请你按照要求完成以下问题:
(1)请直接写出图1中△ABC的面积为
1 ;
(2)动手操作与画图:请你根据所学全等与轴对称知识,在图2的四个网格内完成以下设计轴对称图形的任务,要求如下:
①画出的三角形要与△ABC全等,且它们的顶点都在格点上;
②画出的三角形与△ABC关于某条直线成轴对称图形.
【解析】解:(1)△ABC的面积=×1×2=1,
故答案为:1.
(2)如图所示:
21.(2021春?贵港期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1.
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2.
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是
(a+4,﹣b) .
(4)△ABC的面积为
3 .
【解析】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)点M2的坐标是(a+4,﹣b).
故答案为:(a+4,﹣b).
(4)△ABC的面积为:2×4﹣1×4﹣1×2﹣2×2=8﹣2﹣1﹣2=3.
故答案为:3.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上
13.2画轴对称图形同步练习
一.选择题
1.(2021春?长春期末)在平面直角坐标系中,若点A(2,a)和B(2,7)关于x轴对称,则a的值为( )
A.2
B.﹣2
C.7
D.﹣7
2.(2021春?道县期末)如果点P(m,﹣2,)和点Q(﹣3,n)关于x轴对称,则m+n的值是( )
A.﹣1
B.1
C.﹣5
D.5
3.(2021春?扎兰屯市期末)如果点A(m+2,m﹣1)在x轴上,那么点B(m+3,m﹣2)关于x轴的对称点所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.(2021?泸州)在平面直角坐标系中,将点A(﹣3,﹣2)向右平移5个单位长度得到点B,则点B关于y轴对称点B′的坐标为( )
A.(2,2)
B.(﹣2,2)
C.(﹣2,﹣2)
D.(2,﹣2)
5.若点A的坐标(x,y)满足条件(x﹣3)2+|y+2|=0,则点A关于y轴的对称点的坐标是( )
A.(3,2)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣3,﹣2)
6.(2019春?北海期末)下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A.B.C.D.
7.(2021?荆州)若点P(a+1,2﹣2a)关于x轴的对称点在第四象限,则a的取值范围在数轴上表示为( )
A.
B.
C.
D.
8.若点P(m2﹣2,m)在第一象限的角平分线上,则点(|m|,m﹣1)关于y轴的对称点的坐标是( )
A.(2,)
B.(1,﹣1)
C.(﹣2,)
D.(﹣1,﹣1)
9.(2020秋?太原期末)已知点P(2,﹣4)与点Q(6,﹣4)关于某条直线对称,则这条直线是( )
A.x轴
B.y轴
C.过点(4,0)且垂直于x轴的直线
D.过点(0,﹣4)且平行于x轴的直线
10.下列关于A,B两点的说法中,正确的个数是( )
①如果点A与点B关于y轴对称,则它们的纵坐标相同
②如果点A与点B的纵坐标相同,则它们关于y轴对称
③如果点A与点B的横坐标相同,则它们关于x轴对称
④如果点A与点B关于x轴对称,则它们的横坐标相同
A.1个
B.2个
C.3个
D.4个
二.填空题
11.(2020秋?余干县期中)在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点P',则点P'关于x轴的对称点的坐标为
.
12.(2020秋?吉林期末)在平面直角坐标系中,已知点A的坐标为(﹣2,5),点Q与点A关于y轴对称,点P与点Q关于x轴对称,则点P的坐标是
.
13.(2021春?东湖区期末)点P(m+2,n)向右平移两个单位后得到的点和点Q(n﹣1,2m+1)关于y轴对称,则m+n=
.
14.(2021?天宁区校级模拟)在平面直角坐标系中,若点M(2a+7,0)和N(2﹣b,a+b)关于y轴对称,则ab=
.
15.(2020?海淀区二模)如图,在平面直角坐标系xOy中,已知点C(3,2),将△ABC关于直线x=4对称,得到△A1B1C1,则点C的对应点C1的坐标为
;再将△A1B1C1向上平移一个单位长度,得到△A2B2C2,则点C1的对应点C2的坐标为
.
16.(2018秋?南岸区期末)如图,在平面直角坐标系中,将△ABC三个顶点的横坐标分别乘以﹣1,而纵坐标保持不变,得到△A′B′C′,则△A′B′C′和△ABC关于
对称(横线上填“x轴”、“y轴”或“原点”).
三.解答题
17.(2021春?榆阳区期末)如图,在边长为1的正方形网格中,△ABC的三个顶点都在格点上,在图中画出△ABC关于直线l对称的△A'B'C'.
18.(2021春?射阳县校级期末)如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于直线m对称的△A2B2C2;
(3)△ABC的面积为
.
19.(2021春?清河县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2)C(3,﹣3).
(1)△ABC的面积是
.
(2)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1.
(3)请画出△ABC关于y轴对称的△A2B2C2,并写出点A2、B2、C2的坐标.
20.(2021春?清苑区期末)如图1,已知△ABC的三个顶点均在单位,长度为1的正方形网格中的格点上,请你按照要求完成以下问题:
(1)请直接写出图1中△ABC的面积为
;
(2)动手操作与画图:请你根据所学全等与轴对称知识,在图2的四个网格内完成以下设计轴对称图形的任务,要求如下:
①画出的三角形要与△ABC全等,且它们的顶点都在格点上;
②画出的三角形与△ABC关于某条直线成轴对称图形.
21.(2021春?贵港期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1.
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2.
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是
.
(4)△ABC的面积为
.
答案与解析
一.选择题
1.(2021春?长春期末)在平面直角坐标系中,若点A(2,a)和B(2,7)关于x轴对称,则a的值为( )
A.2
B.﹣2
C.7
D.﹣7
【解析】解:∵点A(2,a)和B(2,7)关于x轴对称,
∴a=﹣7.
故选:D.
2.(2021春?道县期末)如果点P(m,﹣2,)和点Q(﹣3,n)关于x轴对称,则m+n的值是( )
A.﹣1
B.1
C.﹣5
D.5
【解析】解:∵点P(m,﹣2,)和点Q(﹣3,n)关于x轴对称,
∴m=﹣3,n=2,
则m+n=﹣3+2=﹣1.
故选:A.
3.(2021春?扎兰屯市期末)如果点A(m+2,m﹣1)在x轴上,那么点B(m+3,m﹣2)关于x轴的对称点所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【解析】解:∵点A(m+2,m﹣1)在x轴上,
∴m﹣1=0,
即m=1,
∴m+3=4,m﹣2=﹣1,
∴点B(4,﹣1),
∴点B(4,﹣1)在第四象限,
∴点B(4,﹣1)关于x轴的对称点在第一象限,
故选:A.
4.(2021?泸州)在平面直角坐标系中,将点A(﹣3,﹣2)向右平移5个单位长度得到点B,则点B关于y轴对称点B′的坐标为( )
A.(2,2)
B.(﹣2,2)
C.(﹣2,﹣2)
D.(2,﹣2)
【解析】解:点A(﹣3,﹣2)向右平移5个单位长度得到的B的坐标为(﹣3+5,﹣2),即(2,﹣2),
则点B关于y轴的对称点B′的坐标是:(﹣2,﹣2).
故选:C.
5.若点A的坐标(x,y)满足条件(x﹣3)2+|y+2|=0,则点A关于y轴的对称点的坐标是( )
A.(3,2)
B.(﹣3,2)
C.(3,﹣2)
D.(﹣3,﹣2)
【解析】解:由点A的坐标(x,y)满足条件(x﹣3)2+|y+2|=0,得
x﹣3=0,y+2=0.
解得x=3,y=﹣2.即A(3,﹣2).
点A关于y轴的对称点的坐标是(﹣3,﹣2),
故选:D.
6.(2019春?北海期末)下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A.B.C.D.
【解析】解:作△ABC关于直线MN的轴对称图形正确的是B选项,
故选:B.
7.(2021?荆州)若点P(a+1,2﹣2a)关于x轴的对称点在第四象限,则a的取值范围在数轴上表示为( )
A.
B.
C.
D.
【解析】解:∵点P(a+1,2﹣2a)关于x轴的对称点在第四象限,
∴点P在第一象限,
∴,
解得:﹣1<a<1,
在数轴上表示为:,
故选:C.
8.若点P(m2﹣2,m)在第一象限的角平分线上,则点(|m|,m﹣1)关于y轴的对称点的坐标是( )
A.(2,)
B.(1,﹣1)
C.(﹣2,)
D.(﹣1,﹣1)
【解析】解:∵若点P(m2﹣2,m)在第一象限的角平分线上,
∴m2﹣2=m,m>0,
解得:m=2,
∴点(|m|,m﹣1)就是(2,),
∴关于y轴的对称点的坐标是(﹣2,),
故选:C.
9.(2020秋?太原期末)已知点P(2,﹣4)与点Q(6,﹣4)关于某条直线对称,则这条直线是( )
A.x轴
B.y轴
C.过点(4,0)且垂直于x轴的直线
D.过点(0,﹣4)且平行于x轴的直线
【解析】解:点P(2,﹣4)与点Q(6,﹣4)的位置关系是关于直线x=4对称,
故选:C.
10.下列关于A,B两点的说法中,正确的个数是( )
①如果点A与点B关于y轴对称,则它们的纵坐标相同
②如果点A与点B的纵坐标相同,则它们关于y轴对称
③如果点A与点B的横坐标相同,则它们关于x轴对称
④如果点A与点B关于x轴对称,则它们的横坐标相同
A.1个
B.2个
C.3个
D.4个
【解析】解:正确的是:①如果点A与点B关于y轴对称,则它们的纵坐标相同;
④如果点A与点B关于x轴对称,则它们的横坐标相同;
故正确的有两个;
故选:B.
二.填空题
11.(2020秋?余干县期中)在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点P',则点P'关于x轴的对称点的坐标为 (0,﹣2) .
【解析】解:∵将点P(﹣3,2)向右平移3个单位得到点P',
∴点P'坐标为:(0,2),
∴点P'关于x轴的对称点的坐标为(0,﹣2).
故答案为:(0,﹣2).
12.(2020秋?吉林期末)在平面直角坐标系中,已知点A的坐标为(﹣2,5),点Q与点A关于y轴对称,点P与点Q关于x轴对称,则点P的坐标是 (2,﹣5) .
【解析】解:∵点A的坐标为(﹣2,5),点Q与点A关于y轴对称,
∴点Q的坐标为(2,5),
∵点P与点Q关于x轴对称,
∴点P的坐标是(2,﹣5).
故答案为:(2,﹣5).
13.(2021春?东湖区期末)点P(m+2,n)向右平移两个单位后得到的点和点Q(n﹣1,2m+1)关于y轴对称,则m+n= ﹣3 .
【解析】解:点P(m+2,n)向右平移两个单位后得到(m+4,n),
∵点P(m+2,n)向右平移两个单位后得到的点(m+4,n)和点Q(n﹣1,2m+1)关于y轴对称,
∴,
解得:,
故m+n=﹣﹣=﹣3.
故答案为:﹣3.
14.(2021?天宁区校级模拟)在平面直角坐标系中,若点M(2a+7,0)和N(2﹣b,a+b)关于y轴对称,则ab= ﹣27 .
【解析】解:∵点M(2a+7,0)和N(2﹣b,a+b)关于y轴对称,
∴,
解得:,
则ab=(﹣3)3=﹣27.
故答案为:﹣27.
15.(2020?海淀区二模)如图,在平面直角坐标系xOy中,已知点C(3,2),将△ABC关于直线x=4对称,得到△A1B1C1,则点C的对应点C1的坐标为 (5,2) ;再将△A1B1C1向上平移一个单位长度,得到△A2B2C2,则点C1的对应点C2的坐标为 (5,3) .
【解析】解:如图△A1B1C1,△A2B2C2,即为所求.C1(5,2),C2(5,3).
故答案为(5,2),(5,3).
16.(2018秋?南岸区期末)如图,在平面直角坐标系中,将△ABC三个顶点的横坐标分别乘以﹣1,而纵坐标保持不变,得到△A′B′C′,则△A′B′C′和△ABC关于 y轴 对称(横线上填“x轴”、“y轴”或“原点”).
【解析】解:∵横坐标乘以﹣1,
∴横坐标相反,又纵坐标不变,
∴关于y轴对称.
故答案为:y轴.
三.解答题
17.(2021春?榆阳区期末)如图,在边长为1的正方形网格中,△ABC的三个顶点都在格点上,在图中画出△ABC关于直线l对称的△A'B'C'.
【解析】解:如图,△A′B′C′即为所求.
18.(2021春?射阳县校级期末)如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于直线m对称的△A2B2C2;
(3)△ABC的面积为
5.5 .
【解析】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)△ABC的面积=4×3﹣×1×3﹣×4×1﹣×2×3=5.5.
故答案为5.5.
19.(2021春?清河县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2)C(3,﹣3).
(1)△ABC的面积是
3.5 .
(2)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1.
(3)请画出△ABC关于y轴对称的△A2B2C2,并写出点A2、B2、C2的坐标.
【解析】解:(1)根据A(2,﹣1),B(1,﹣2)C(3,﹣3).
∴△ABC的面积=2×2﹣1×11×21×2=1.5;
故答案为:1.5;
(2)如图,△A1B1C1即为所求;
(3)△A2B2C2即为所求;A2(﹣2,﹣1),B2(﹣1,﹣2),C2(﹣3,﹣3).
20.(2021春?清苑区期末)如图1,已知△ABC的三个顶点均在单位,长度为1的正方形网格中的格点上,请你按照要求完成以下问题:
(1)请直接写出图1中△ABC的面积为
1 ;
(2)动手操作与画图:请你根据所学全等与轴对称知识,在图2的四个网格内完成以下设计轴对称图形的任务,要求如下:
①画出的三角形要与△ABC全等,且它们的顶点都在格点上;
②画出的三角形与△ABC关于某条直线成轴对称图形.
【解析】解:(1)△ABC的面积=×1×2=1,
故答案为:1.
(2)如图所示:
21.(2021春?贵港期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1.
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2.
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是
(a+4,﹣b) .
(4)△ABC的面积为
3 .
【解析】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)点M2的坐标是(a+4,﹣b).
故答案为:(a+4,﹣b).
(4)△ABC的面积为:2×4﹣1×4﹣1×2﹣2×2=8﹣2﹣1﹣2=3.
故答案为:3.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
