13.4 课题学习 最短路径问题同步练习(含解析)
文档属性
| 名称 | 13.4 课题学习 最短路径问题同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:40:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级上
13.4课题学习
最短路径问题同步练习
一.选择题
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A.B.
C.D.
2.如图,∠AOB=60°,点M为∠AOB内一点,点M、N分别在OA、OB上,当△PMN周长最小时,∠MPN的度数是( )
A.120°
B.60°
C.30°
D.90°
3.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.B.C.D.
4.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2
B.4
C.5
D.6
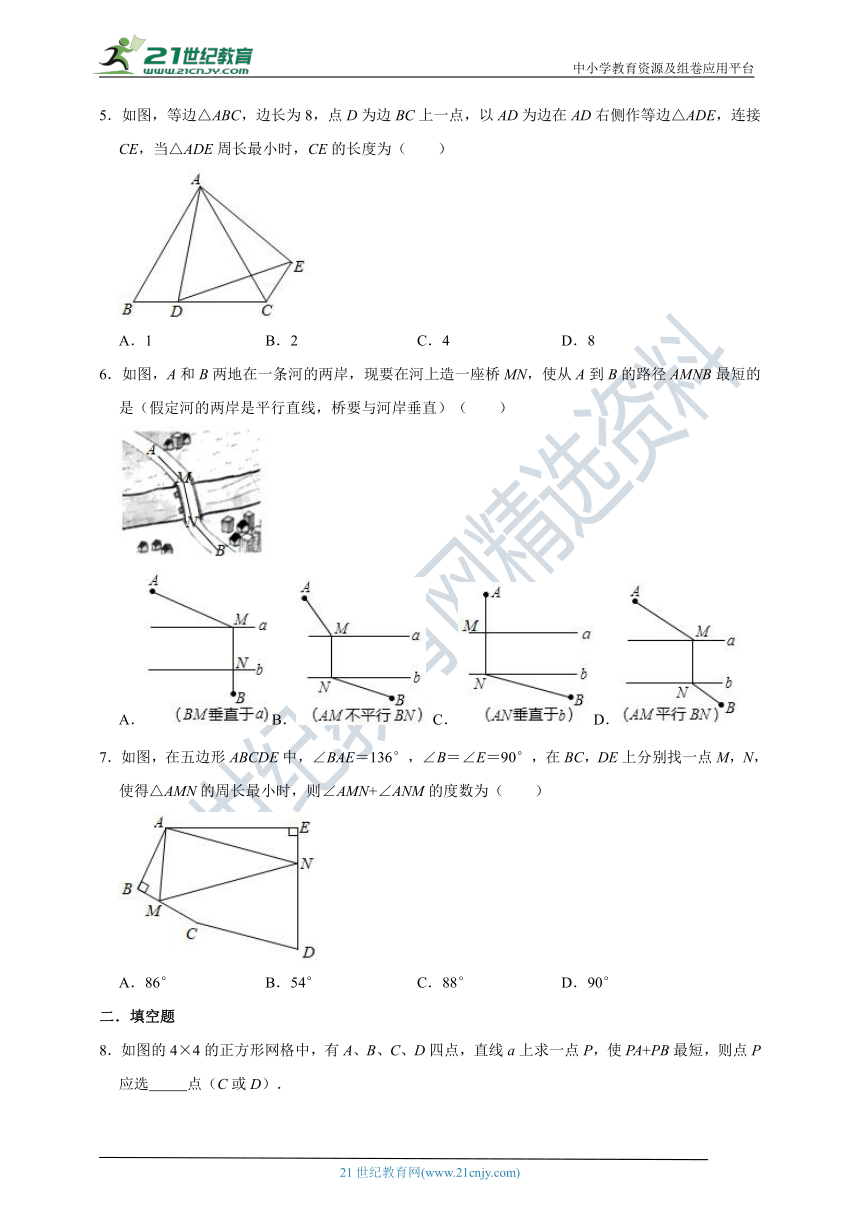
5.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A.1
B.2
C.4
D.8
6.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.B.
C.D.
7.如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.86°
B.54°
C.88°
D.90°
二.填空题
8.如图的4×4的正方形网格中,有A、B、C、D四点,直线a上求一点P,使PA+PB最短,则点P应选
点(C或D).
9.如图∠AOB=30°,∠AOB内有一定点P,且OP=15,若在OA、OB上分别有动点M、N,则△PMN周长的最小值是
.
10.如图,锐角△ABC的边AC=6,△ABC的面积为15,AD平分∠BAC交BC于D,M,N分别是AD和AB上的动点,则BM+MN的最小值是
.
11.小镇A与B在公路同侧,如图,A到公路的距离为45里,要在公路边建一个货站,及货站到A、B的两条乡道,经计算,两条乡道总长最短可为140里,此时两条乡道的夹角为120°,则B到公路的距离为
里.
12.如图,Rt△ABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是
.
三.解答题
13.如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短.
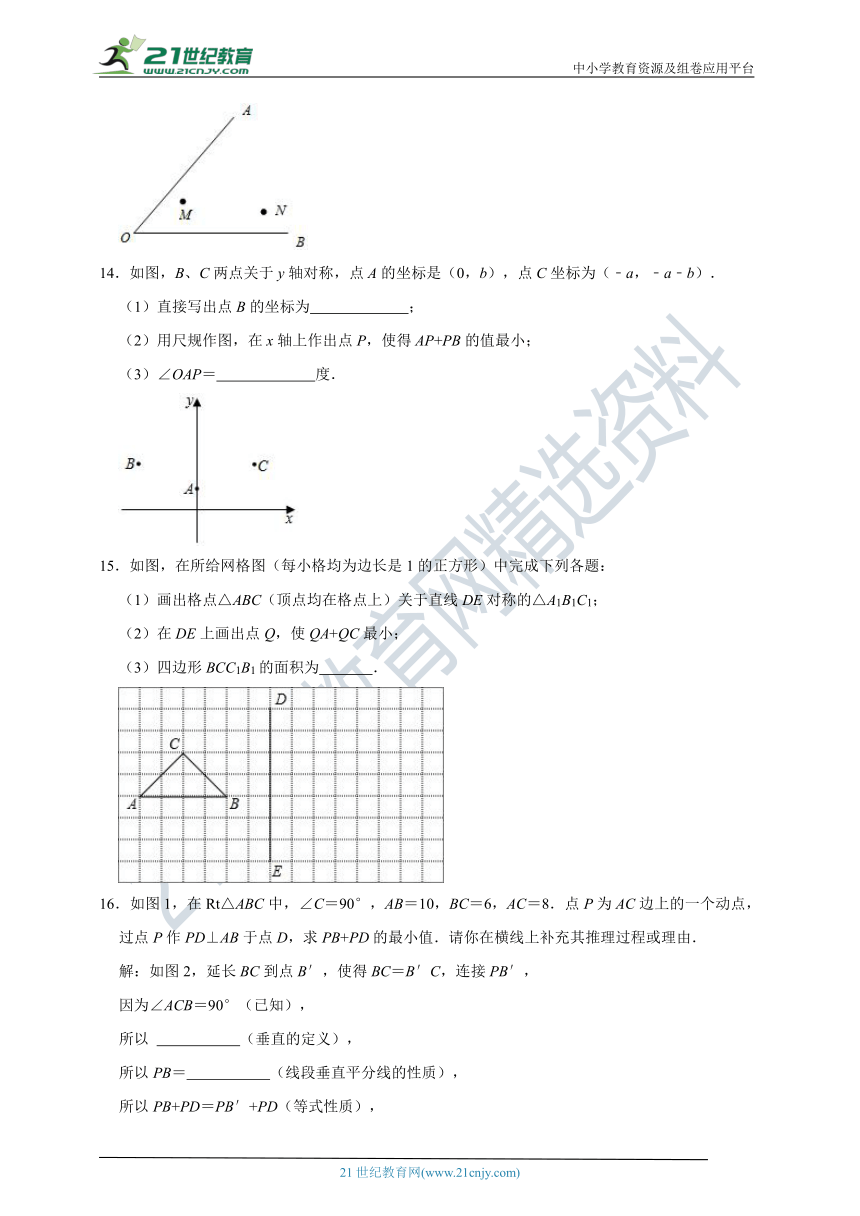
14.如图,B、C两点关于y轴对称,点A的坐标是(0,b),点C坐标为(﹣a,﹣a﹣b).
(1)直接写出点B的坐标为
;
(2)用尺规作图,在x轴上作出点P,使得AP+PB的值最小;
(3)∠OAP=
度.
15.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小;
(3)四边形BCC1B1的面积为
.
16.如图1,在Rt△ABC中,∠C=90°,AB=10,BC=6,AC=8.点P为AC边上的一个动点,过点P作PD⊥AB于点D,求PB+PD的最小值.请你在横线上补充其推理过程或理由.
解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以
(垂直的定义),
所以PB=
(线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC,
,
所以△ABC≌△AB′C(理由:
),
所以SABB′=S△ABC+
=2S△ABC(全等三角形面积相等),
因为S△ABB′=×AB×B'D=×10×B′D=5B′D,
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48,
所以
(同一三角形面积相等),
所以B′D=,
所以
.
17.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠AMN的度数是
.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.
18.在等边三角形ABC中,AD是BC边上的高,E为AC的中点,P为AD上一动点,若AD=12,试求PC+PE的最小值.
答案与解析
一.选择题
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A.B.
C.D.
【解析】解:∵点A,B在直线l的同侧,
∴作A点关于l的对称点A',连接A'B与l的交点为P,
由对称性可知AP=A'P,
∴AP+PB≥A'P,
∴当A、P、B三点共线时PA+PB最小,
故选:B.
2.如图,∠AOB=60°,点M为∠AOB内一点,点M、N分别在OA、OB上,当△PMN周长最小时,∠MPN的度数是( )
A.120°
B.60°
C.30°
D.90°
【解析】解:分别作点P关于OA、OB的对称点P1、P2,连接P1、P2交OA于M,交OB于N,
∴OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,
根据轴对称的性质可得MP=P1M,PN=P2N,
∴△PMN的周长的最小值=P1P2,
由轴对称的性质可得∠P1OP2=2∠AOB=2∠O,
∴等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2∠O,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=∠OP1P2+∠OP2P1=180°﹣2∠O=60°,
故选:B.
3.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.B.C.D.
【解析】解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
4.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2
B.4
C.5
D.6
【解析】解:作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,
∴CE+EF=C'E+EF≥C'F,
∴CE+EF的最小值C'F的长,
∴CC'⊥BD,
∵BD平分∠ABC,
∴∠C'BG=∠GBC,
在△C'BG和△CBG中,
,
∴△C'BG≌△CBG(ASA),
∴BC=BC',
∵AC=BC=8,∠ACB=120°,
∴∠ABC=30°,BC'=8,
在Rt△BCC'中,C'F=BC'?sin30°=8×=4,
∴CE+EF的最小值为4,
故选:B.
5.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A.1
B.2
C.4
D.8
【解析】解:
∵△ADE是等边三角形,
∴AD=DE=AE,
∴C△ADE=3AD,
当△ADE周长最小时,
即AD最小,
当AD⊥BC时,AD最小,
此时,BD=AB=4,
∵△ABC是等边三角形,
∴∠1+∠2=60°,
又∵∠2+∠3=60°,
∴∠1=∠3,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE=4,
故选:C.
6.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.B.
C.D.
【解析】解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),
只要AM+BN最短就行,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.连接IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
7.如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.86°
B.54°
C.88°
D.90°
【解析】解:如图,作点A关于BC的对称点P,关于DE的对称点Q,连接PQ与BC相交于点M,与DE相交于点N,
则AM=PM,AN=QN,
所以,∠P=∠PAM,∠Q=∠QAN,
所以,△AMN周长=AM+MN+AN=PM+MN+QN=PQ,
由轴对称确定最短路线,PQ的长度即为△AMN的周长最小值,
∵∠BAE=136°,
∴∠P+∠Q=180°﹣136°=44°,
∵∠AMN=∠P+∠PAM=2∠P,∠ANM=∠Q+∠QAN=2∠Q,
∴∠AMN+∠ANM=2(∠P+∠Q)=2×44°=88°,
故选:C.
二.填空题
8.如图的4×4的正方形网格中,有A、B、C、D四点,直线a上求一点P,使PA+PB最短,则点P应选 C 点(C或D).
【解析】解:如图,点A′是点A关于直线a的对称点,连接A′B,则A′B与直线a的交点,即为点P,此时PA+PB最短,
∵A′B与直线a交于点C,
∴点P应选C点.
故答案为:C.
9.如图∠AOB=30°,∠AOB内有一定点P,且OP=15,若在OA、OB上分别有动点M、N,则△PMN周长的最小值是 15 .
【解析】解:作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB于N,连接PM,PN,则此时△PMN的周长最小,
连接OD,OE,
∵P、D关于OA对称,
∴OD=OP,PM=DM,
同理OE=OP,PN=EN,
∴OD=OE=OP=15,
∵P、D关于OA对称,
∴OA⊥PD,
∵OD=OP,
∴∠DOA=∠POA,
同理∠POB=∠EOB,
∴∠DOE=2∠AOB=2×30°═60°,
∵OD=OE=15,
∴△DOE是等边三角形,
∴DE=15,
即△PMN的周长是PM+MN+PN=DM+MN+EN=DE=15,
故答案为15.
10.如图,锐角△ABC的边AC=6,△ABC的面积为15,AD平分∠BAC交BC于D,M,N分别是AD和AB上的动点,则BM+MN的最小值是 5 .
【解析】解:作N关于AD的对称点为R,作AC边上的高BE(E在AC上),
∵AD平分∠CAB,△ABC为锐角三角形,
∴R必在AC上,
∵N关于AD的对称点为R,
∴MR=MN,
∴BM+MN=BM+MR,
即BM+MN=BR≥BE(垂线段最短),
∵△ABC的面积是15,AC=6,
∴×6×BE=15,
∴BE=5,
即BM+MN的最小值为5.
11.小镇A与B在公路同侧,如图,A到公路的距离为45里,要在公路边建一个货站,及货站到A、B的两条乡道,经计算,两条乡道总长最短可为140里,此时两条乡道的夹角为120°,则B到公路的距离为 25 里.
【解析】解:如图,作A关于直线l的对称点A'交直线l于D,连接A'B交直线l于P,连接AP,过B分别作BE⊥l交l于E、作BC⊥AA'交AA'于C,
∵∠CDE=∠DEB=∠BCD=90°,
∴四边形CDBE为矩形,
∴BE=CD,
由题得:A'D=45(里),A'B=140(里),∠APB=120°,
∵∠APD=∠A'PD=∠BPE,
∴∠A'PD=(180°﹣120°)÷2=30°,
∵BC∥DE,
∴∠A'BC=30°,
∴A'C=A'B=70(里),
∴CD=BE=70﹣45=25(里).
故答案为:25.
12.如图,Rt△ABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是 16 .
【解析】解:作A关于BC的对称点A',连接A′D,
则A′D的长度就是AP+DP的最小值,
连接A′B,
∵BC⊥AA′,AC=A′C
∴AB=A′B,AP=A′P,
∵∠ACB=90°,∠ABC=30°
∴∠A=60°,
∴△AA'B为等边三角形,
∴A′D=BC=16,
∴AP+DP=A'P+PD=A′D=16,
∴AP+DP的最小值是16,
故答案为:16.
三.解答题
13.如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短.
【解析】解:如图:
作点M关于OA的对称点M′,作点N关于OB的对称点N′,
连接M′N′交OA于P、交OB于Q,则M→P→Q→N为最短路线.
14.如图,B、C两点关于y轴对称,点A的坐标是(0,b),点C坐标为(﹣a,﹣a﹣b).
(1)直接写出点B的坐标为 (a,﹣a﹣b) ;
(2)用尺规作图,在x轴上作出点P,使得AP+PB的值最小;
(3)∠OAP= 45 度.
【解析】解:(1)点B的坐标为(a,﹣a﹣b);
故答案为:(a,﹣a﹣b).
(2)如图所示,点P即为所求;
(3)过B作BD⊥y轴于D,D(0,﹣a﹣b),
则BD=﹣a,OD=﹣a﹣b,
由(2)知A与A′关于x轴对称,
∴A′O=AO=b,
∴A′D=BD,
在Rt△A′DB中,∠A′DB=90°,A′P=AP,
∴∠BA′D=∠B=45°,
∵A与A′关于x轴对称,
∴∠OAP=∠DA′P=45°.
故答案为:45.
15.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小;
(3)四边形BCC1B1的面积为 12 .
【解析】解:(1)如图所示:
;
(2)如图所示:
;
(3)
∵每小格均为边长是1的正方形,
∴CC1=4+4=8,BB1=2+2=4,BB1和CC1之间的距离为2,
∴四边形BCC1B1的面积为×(8+4)×2=12,
故答案为:12.
16.如图1,在Rt△ABC中,∠C=90°,AB=10,BC=6,AC=8.点P为AC边上的一个动点,过点P作PD⊥AB于点D,求PB+PD的最小值.请你在横线上补充其推理过程或理由.
解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以
AC⊥BB' (垂直的定义),
所以PB= PB' (线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC, BC=B′C ,
所以△ABC≌△AB′C(理由: SAS ),
所以SABB′=S△ABC+ S△AB'C =2S△ABC(全等三角形面积相等),
因为S△ABB′=×AB×B'D=×10×B′D=5B′D,
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48,
所以
(同一三角形面积相等),
所以B′D=,
所以
PB+PD的最小值为 .
【解析】解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以
AC⊥BB'(垂直的定义),
所以PB=PB'(线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC,BC=B′C,
所以△ABC≌△AB′C(理由:SAS),
所以SABB′=S△ABC+S△AB'C=2S△ABC(全等三角形面积相等),
因为S△ABB′=×AB×B'D=×10×B′D=5B′D,
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48,
所以
(同一三角形面积相等),
所以B′D=,
所以
PB+PD的最小值为.
故答案为:AC⊥BB';PB';BC=B′C;SAS;S△AB'C;;PB+PD的最小值为.
17.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠AMN的度数是 50° .
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.
【解析】解:(1)∵AB=AC,
∴∠C=∠ABC=70°,
∴∠A=40°,
∵AB的垂直平分线交AB于点N,
∴∠ANM=90°,
∴∠NMA=50°,
故答案为:50°;
(2)①∵MN是AB的垂直平分线,
∴AM=BM,
∴△BCM的周长=BM+CM+BC=AM+MC+BC=AC+BC,
∵AB=AC=8cm,△MBC的周长是14cm,
∴BC=14﹣8=6(cm);
②当P与M重合时,△PBC的周长最小.
理由:∵PB+PC=PA+PC,PA+PC≥AC,
∴当P与M重合时,PA+PC=AC,此时PB+PC最小值等于AC的长,
∴△PBC的周长最小值=AC+BC=8+6=14(cm).
18.在等边三角形ABC中,AD是BC边上的高,E为AC的中点,P为AD上一动点,若AD=12,试求PC+PE的最小值.
【解析】解:如图,连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵AD=12,点E是边AC的中点,
∴AD=BE=12,
∴PE+PC的最小值是12.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上
13.4课题学习
最短路径问题同步练习
一.选择题
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A.B.
C.D.
2.如图,∠AOB=60°,点M为∠AOB内一点,点M、N分别在OA、OB上,当△PMN周长最小时,∠MPN的度数是( )
A.120°
B.60°
C.30°
D.90°
3.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.B.C.D.
4.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2
B.4
C.5
D.6
5.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A.1
B.2
C.4
D.8
6.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.B.
C.D.
7.如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.86°
B.54°
C.88°
D.90°
二.填空题
8.如图的4×4的正方形网格中,有A、B、C、D四点,直线a上求一点P,使PA+PB最短,则点P应选
点(C或D).
9.如图∠AOB=30°,∠AOB内有一定点P,且OP=15,若在OA、OB上分别有动点M、N,则△PMN周长的最小值是
.
10.如图,锐角△ABC的边AC=6,△ABC的面积为15,AD平分∠BAC交BC于D,M,N分别是AD和AB上的动点,则BM+MN的最小值是
.
11.小镇A与B在公路同侧,如图,A到公路的距离为45里,要在公路边建一个货站,及货站到A、B的两条乡道,经计算,两条乡道总长最短可为140里,此时两条乡道的夹角为120°,则B到公路的距离为
里.
12.如图,Rt△ABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是
.
三.解答题
13.如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短.
14.如图,B、C两点关于y轴对称,点A的坐标是(0,b),点C坐标为(﹣a,﹣a﹣b).
(1)直接写出点B的坐标为
;
(2)用尺规作图,在x轴上作出点P,使得AP+PB的值最小;
(3)∠OAP=
度.
15.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小;
(3)四边形BCC1B1的面积为
.
16.如图1,在Rt△ABC中,∠C=90°,AB=10,BC=6,AC=8.点P为AC边上的一个动点,过点P作PD⊥AB于点D,求PB+PD的最小值.请你在横线上补充其推理过程或理由.
解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以
(垂直的定义),
所以PB=
(线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC,
,
所以△ABC≌△AB′C(理由:
),
所以SABB′=S△ABC+
=2S△ABC(全等三角形面积相等),
因为S△ABB′=×AB×B'D=×10×B′D=5B′D,
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48,
所以
(同一三角形面积相等),
所以B′D=,
所以
.
17.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠AMN的度数是
.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.
18.在等边三角形ABC中,AD是BC边上的高,E为AC的中点,P为AD上一动点,若AD=12,试求PC+PE的最小值.
答案与解析
一.选择题
1.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A.B.
C.D.
【解析】解:∵点A,B在直线l的同侧,
∴作A点关于l的对称点A',连接A'B与l的交点为P,
由对称性可知AP=A'P,
∴AP+PB≥A'P,
∴当A、P、B三点共线时PA+PB最小,
故选:B.
2.如图,∠AOB=60°,点M为∠AOB内一点,点M、N分别在OA、OB上,当△PMN周长最小时,∠MPN的度数是( )
A.120°
B.60°
C.30°
D.90°
【解析】解:分别作点P关于OA、OB的对称点P1、P2,连接P1、P2交OA于M,交OB于N,
∴OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,
根据轴对称的性质可得MP=P1M,PN=P2N,
∴△PMN的周长的最小值=P1P2,
由轴对称的性质可得∠P1OP2=2∠AOB=2∠O,
∴等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2∠O,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=∠OP1P2+∠OP2P1=180°﹣2∠O=60°,
故选:B.
3.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.B.C.D.
【解析】解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
4.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2
B.4
C.5
D.6
【解析】解:作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,
∴CE+EF=C'E+EF≥C'F,
∴CE+EF的最小值C'F的长,
∴CC'⊥BD,
∵BD平分∠ABC,
∴∠C'BG=∠GBC,
在△C'BG和△CBG中,
,
∴△C'BG≌△CBG(ASA),
∴BC=BC',
∵AC=BC=8,∠ACB=120°,
∴∠ABC=30°,BC'=8,
在Rt△BCC'中,C'F=BC'?sin30°=8×=4,
∴CE+EF的最小值为4,
故选:B.
5.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A.1
B.2
C.4
D.8
【解析】解:
∵△ADE是等边三角形,
∴AD=DE=AE,
∴C△ADE=3AD,
当△ADE周长最小时,
即AD最小,
当AD⊥BC时,AD最小,
此时,BD=AB=4,
∵△ABC是等边三角形,
∴∠1+∠2=60°,
又∵∠2+∠3=60°,
∴∠1=∠3,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE=4,
故选:C.
6.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.B.
C.D.
【解析】解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),
只要AM+BN最短就行,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.连接IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
7.如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.86°
B.54°
C.88°
D.90°
【解析】解:如图,作点A关于BC的对称点P,关于DE的对称点Q,连接PQ与BC相交于点M,与DE相交于点N,
则AM=PM,AN=QN,
所以,∠P=∠PAM,∠Q=∠QAN,
所以,△AMN周长=AM+MN+AN=PM+MN+QN=PQ,
由轴对称确定最短路线,PQ的长度即为△AMN的周长最小值,
∵∠BAE=136°,
∴∠P+∠Q=180°﹣136°=44°,
∵∠AMN=∠P+∠PAM=2∠P,∠ANM=∠Q+∠QAN=2∠Q,
∴∠AMN+∠ANM=2(∠P+∠Q)=2×44°=88°,
故选:C.
二.填空题
8.如图的4×4的正方形网格中,有A、B、C、D四点,直线a上求一点P,使PA+PB最短,则点P应选 C 点(C或D).
【解析】解:如图,点A′是点A关于直线a的对称点,连接A′B,则A′B与直线a的交点,即为点P,此时PA+PB最短,
∵A′B与直线a交于点C,
∴点P应选C点.
故答案为:C.
9.如图∠AOB=30°,∠AOB内有一定点P,且OP=15,若在OA、OB上分别有动点M、N,则△PMN周长的最小值是 15 .
【解析】解:作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB于N,连接PM,PN,则此时△PMN的周长最小,
连接OD,OE,
∵P、D关于OA对称,
∴OD=OP,PM=DM,
同理OE=OP,PN=EN,
∴OD=OE=OP=15,
∵P、D关于OA对称,
∴OA⊥PD,
∵OD=OP,
∴∠DOA=∠POA,
同理∠POB=∠EOB,
∴∠DOE=2∠AOB=2×30°═60°,
∵OD=OE=15,
∴△DOE是等边三角形,
∴DE=15,
即△PMN的周长是PM+MN+PN=DM+MN+EN=DE=15,
故答案为15.
10.如图,锐角△ABC的边AC=6,△ABC的面积为15,AD平分∠BAC交BC于D,M,N分别是AD和AB上的动点,则BM+MN的最小值是 5 .
【解析】解:作N关于AD的对称点为R,作AC边上的高BE(E在AC上),
∵AD平分∠CAB,△ABC为锐角三角形,
∴R必在AC上,
∵N关于AD的对称点为R,
∴MR=MN,
∴BM+MN=BM+MR,
即BM+MN=BR≥BE(垂线段最短),
∵△ABC的面积是15,AC=6,
∴×6×BE=15,
∴BE=5,
即BM+MN的最小值为5.
11.小镇A与B在公路同侧,如图,A到公路的距离为45里,要在公路边建一个货站,及货站到A、B的两条乡道,经计算,两条乡道总长最短可为140里,此时两条乡道的夹角为120°,则B到公路的距离为 25 里.
【解析】解:如图,作A关于直线l的对称点A'交直线l于D,连接A'B交直线l于P,连接AP,过B分别作BE⊥l交l于E、作BC⊥AA'交AA'于C,
∵∠CDE=∠DEB=∠BCD=90°,
∴四边形CDBE为矩形,
∴BE=CD,
由题得:A'D=45(里),A'B=140(里),∠APB=120°,
∵∠APD=∠A'PD=∠BPE,
∴∠A'PD=(180°﹣120°)÷2=30°,
∵BC∥DE,
∴∠A'BC=30°,
∴A'C=A'B=70(里),
∴CD=BE=70﹣45=25(里).
故答案为:25.
12.如图,Rt△ABC中,∠C=90°,∠B=30°,BC=16,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是 16 .
【解析】解:作A关于BC的对称点A',连接A′D,
则A′D的长度就是AP+DP的最小值,
连接A′B,
∵BC⊥AA′,AC=A′C
∴AB=A′B,AP=A′P,
∵∠ACB=90°,∠ABC=30°
∴∠A=60°,
∴△AA'B为等边三角形,
∴A′D=BC=16,
∴AP+DP=A'P+PD=A′D=16,
∴AP+DP的最小值是16,
故答案为:16.
三.解答题
13.如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短.
【解析】解:如图:
作点M关于OA的对称点M′,作点N关于OB的对称点N′,
连接M′N′交OA于P、交OB于Q,则M→P→Q→N为最短路线.
14.如图,B、C两点关于y轴对称,点A的坐标是(0,b),点C坐标为(﹣a,﹣a﹣b).
(1)直接写出点B的坐标为 (a,﹣a﹣b) ;
(2)用尺规作图,在x轴上作出点P,使得AP+PB的值最小;
(3)∠OAP= 45 度.
【解析】解:(1)点B的坐标为(a,﹣a﹣b);
故答案为:(a,﹣a﹣b).
(2)如图所示,点P即为所求;
(3)过B作BD⊥y轴于D,D(0,﹣a﹣b),
则BD=﹣a,OD=﹣a﹣b,
由(2)知A与A′关于x轴对称,
∴A′O=AO=b,
∴A′D=BD,
在Rt△A′DB中,∠A′DB=90°,A′P=AP,
∴∠BA′D=∠B=45°,
∵A与A′关于x轴对称,
∴∠OAP=∠DA′P=45°.
故答案为:45.
15.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小;
(3)四边形BCC1B1的面积为 12 .
【解析】解:(1)如图所示:
;
(2)如图所示:
;
(3)
∵每小格均为边长是1的正方形,
∴CC1=4+4=8,BB1=2+2=4,BB1和CC1之间的距离为2,
∴四边形BCC1B1的面积为×(8+4)×2=12,
故答案为:12.
16.如图1,在Rt△ABC中,∠C=90°,AB=10,BC=6,AC=8.点P为AC边上的一个动点,过点P作PD⊥AB于点D,求PB+PD的最小值.请你在横线上补充其推理过程或理由.
解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以
AC⊥BB' (垂直的定义),
所以PB= PB' (线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC, BC=B′C ,
所以△ABC≌△AB′C(理由: SAS ),
所以SABB′=S△ABC+ S△AB'C =2S△ABC(全等三角形面积相等),
因为S△ABB′=×AB×B'D=×10×B′D=5B′D,
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48,
所以
(同一三角形面积相等),
所以B′D=,
所以
PB+PD的最小值为 .
【解析】解:如图2,延长BC到点B′,使得BC=B′C,连接PB′,
因为∠ACB=90°(已知),
所以
AC⊥BB'(垂直的定义),
所以PB=PB'(线段垂直平分线的性质),
所以PB+PD=PB′+PD(等式性质),
所以过点B′作B′D⊥AB于点D,交AC于点P,此时PB+PD取最小值,连接AB′.
在△ABC和△AB′C中,
因为∠ACB=∠ACB′=90°,AC=AC,BC=B′C,
所以△ABC≌△AB′C(理由:SAS),
所以SABB′=S△ABC+S△AB'C=2S△ABC(全等三角形面积相等),
因为S△ABB′=×AB×B'D=×10×B′D=5B′D,
又因为S△ABB′=2S△ABC=2××BC×AC=2××6×8=48,
所以
(同一三角形面积相等),
所以B′D=,
所以
PB+PD的最小值为.
故答案为:AC⊥BB';PB';BC=B′C;SAS;S△AB'C;;PB+PD的最小值为.
17.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠AMN的度数是 50° .
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.
【解析】解:(1)∵AB=AC,
∴∠C=∠ABC=70°,
∴∠A=40°,
∵AB的垂直平分线交AB于点N,
∴∠ANM=90°,
∴∠NMA=50°,
故答案为:50°;
(2)①∵MN是AB的垂直平分线,
∴AM=BM,
∴△BCM的周长=BM+CM+BC=AM+MC+BC=AC+BC,
∵AB=AC=8cm,△MBC的周长是14cm,
∴BC=14﹣8=6(cm);
②当P与M重合时,△PBC的周长最小.
理由:∵PB+PC=PA+PC,PA+PC≥AC,
∴当P与M重合时,PA+PC=AC,此时PB+PC最小值等于AC的长,
∴△PBC的周长最小值=AC+BC=8+6=14(cm).
18.在等边三角形ABC中,AD是BC边上的高,E为AC的中点,P为AD上一动点,若AD=12,试求PC+PE的最小值.
【解析】解:如图,连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵AD=12,点E是边AC的中点,
∴AD=BE=12,
∴PE+PC的最小值是12.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
