2021-2022学年鲁教五四新版七年级上册数学《第1章 三角形》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教五四新版七年级上册数学《第1章 三角形》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 209.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 10:22:38 | ||
图片预览




文档简介
2021-2022学年鲁教五四新版七年级上册数学《第1章
三角形》单元测试卷
一.选择题
1.如图所示,三角形的个数是( )
A.3
B.4
C.5
D.6
2.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③
B.①②
C.②③
D.①③
3.三角形的重心是三角形三条( )的交点.
A.中线
B.高
C.角平分线
D.垂直平分线
4.三角形按边分类可分为( )
A.不等边三角形、等边三角形
B.等腰三角形、等边三角形
C.不等边三角形、等腰三角形、等边三角形
D.不等边三角形、等腰三角形
5.在三角形ABC中,AB=7,BC=2,并且AC的长为奇数,则AC=( )
A.3
B.5
C.7
D.9
6.如图,在△ABC中,∠B=70°,沿图中虚线EF翻折,使得点B落在AC上的点D处,则∠1+∠2等于( )
A.160°
B.150°
C.140°
D.110°
7.三角形的三个外角的和是( )
A.90°
B.180°
C.270°
D.360°
8.若△ABC中,∠A=90°,且∠B﹣∠C=30°,那么∠C的度数为( )
A.30°
B.40°
C.50°
D.60°
9.如图,称有一条公共边的两个三角形为一对共边三角形,则图中的共边三角形有( )对.
A.8
B.16
C.24
D.32
10.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3
B.
C.
D.6
二.填空题
11.如图,四边形ABCD中,E,F,G,H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为4、5、6,四边形DHOG的面积为
.
12.已知三角形两边长为2和7,则第三边a的取值范围为
.
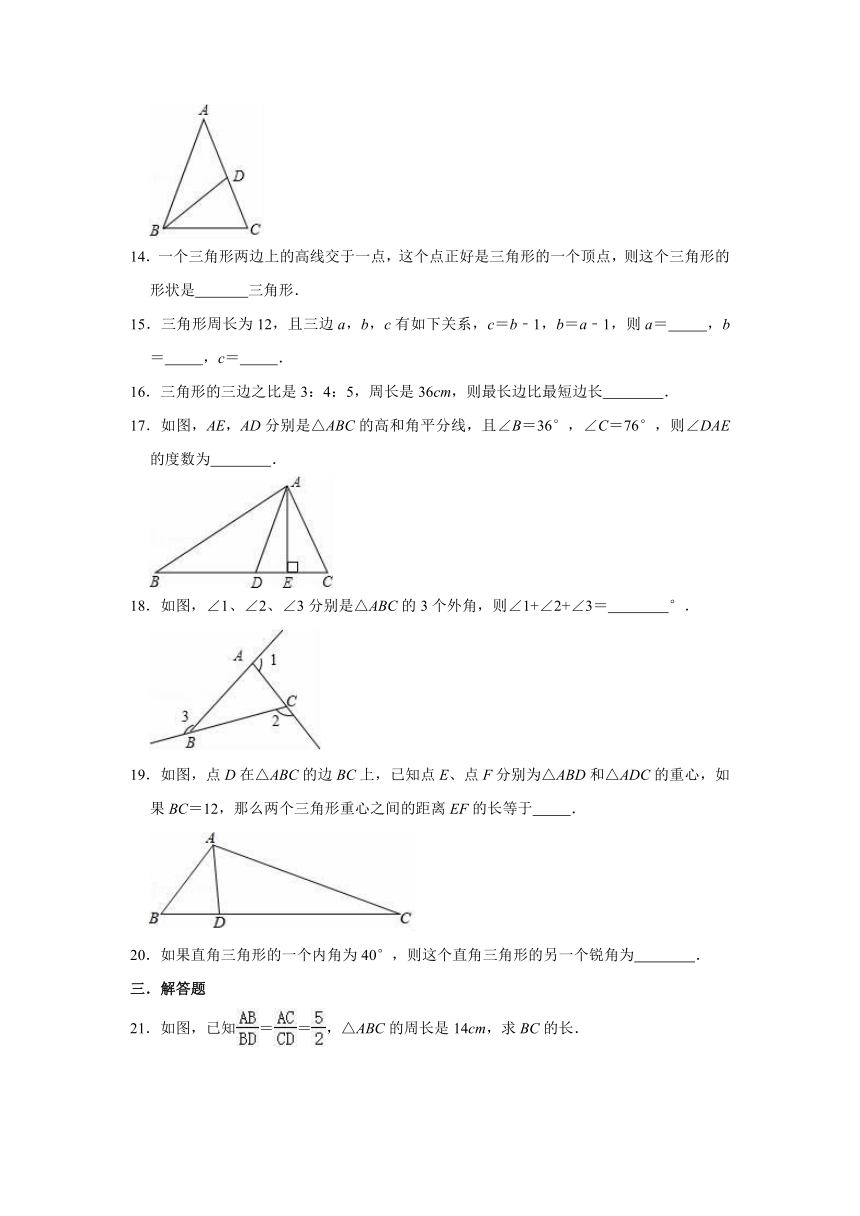
13.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是
.
14.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是
三角形.
15.三角形周长为12,且三边a,b,c有如下关系,c=b﹣1,b=a﹣1,则a=
,b=
,c=
.
16.三角形的三边之比是3:4:5,周长是36cm,则最长边比最短边长
.
17.如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为
.
18.如图,∠1、∠2、∠3分别是△ABC的3个外角,则∠1+∠2+∠3=
°.
19.如图,点D在△ABC的边BC上,已知点E、点F分别为△ABD和△ADC的重心,如果BC=12,那么两个三角形重心之间的距离EF的长等于
.
20.如果直角三角形的一个内角为40°,则这个直角三角形的另一个锐角为
.
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
23.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
24.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BED=55°,求∠BAD的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为20,BD=2.5,求△BDE中BD边上的高.
25.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
26.已知a、b、c为三角形三边的长,化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|.
27.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
参考答案与试题解析
一.选择题
1.解:如图所示:
三角形有△AED、△BED、△ACD、△ABD、△ABC,共5个.
故选:C.
2.解:①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故选:B.
3.解:三角形的重心是三角形三条中线的交点.
故选:A.
4.解:三角形按边分类可分为不等边三角形、等腰三角形,
故选:D.
5.解:∵AB=7,BC=2,
∴7+2=9,7﹣2=5,
∴5<AC<9,
∵AC为奇数,
∴AC=7.
故选:C.
6.解:∵∠B=70°,
∴∠BEF+∠BFE=110°,
∵翻折,
∴∠BEF=∠DEF,∠BFE=∠DFE,
∴∠BED+∠BFD=2(∠BEF+∠BFE)=2×110°=220°,
∴∠1+∠2=180°×2﹣220°=140°,
故选:C.
7.解:根据三角形外角的性质,可得三角形的三个外角的和是360°.
故选:D.
8.解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B﹣∠C=30°,
∴∠B=60°,∠C=30°,
故选:A.
9.解:以AB为公共边的三角形有:△ABD和△ABC;
以AC为公共边的三角形有:△ACE和△ACB;
以AD为公共边的三角形有:△ADE和△ABD;
以AE为公共边的三角形有:△AED和△AEC;
以BC为公共边的三角形有:△BCO和△BCA和△BCD和△BCE,4个三角形中任何两个都是共边三角形,有6对;
以BD为公共边的三角形有:△BDC,△BDE,BDA任何两个都是3对共边三角形;
以BE为公共边的三角形有:△BEO,△BED,△BEC任何两个都是3对共边三角形.
以OB为公共边的三角形有:△OBE和△OBC;
以CD为公共边的三角形有:△CDO和△CDB和△CDE任何两个都是3对共边三角形.
以CE为公共边的三角形有:△CED,△CEA,△CEB任何两个都是3对共边三角形;
以CO为公共边的三角形有:△COD和△COB;
以DE为公共边的三角形有:△AED和△OED和△BED和三角CED,4个三角形中任何两个都是共边三角形,有6对;
以OD为公共边的三角形有:△ODC和△ODE;
以OE为公共边的三角形有:△OBE和△ODE.
共32对.
故选:D.
10.解:∵S△ABC=BC?hBC=AC?hAC=18,
∴S△ABC=(BD+CD)?hBC=(AE+CE)?hAC=18,
∵AE=CE=AC,S△AEB=AE?hAC,S△BCE=EC?hAC,
∴S△AEB=S△CEB=S△ABC=×18=9,
即S△AEF+S△ABF=9①,
同理:∵BD=2CD,BD+CD=BC,
∴BD=BC,S△ABD=BD?hBC,
∴S△ABD=S△ABC=×18=12,
即S△BDF+S△ABF=12②,
①﹣②得:S△BDF﹣SAEF=(S△BDF+S△ABF)﹣(S△AEF+S△ABF)=12﹣9=3,
故选:A.
二.填空题
11.解:连接OC,OB,OA,OD,
∵E、F、G、H依次是各边中点,
∴△AOE和△BOE等底等高,所以S△OAE=S△OBE,
同理可证,S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,
∵S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,
∴4+6=5+S四边形DHOG,
解得S四边形DHOG=5.
故答案是:5.
12.解:∵7﹣2=5,2+7=9,
∴第三边a的取值范围为5<a<9.
故答案为:5<a<9.
13.解:∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为11,AB=5,BC=3,
∴△BCD的周长是11﹣(5﹣3)=9,
故答案为9.
14.解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
15.解:∵c=b﹣1,b=a﹣1,
∴c=a﹣1﹣1=a﹣2,
又∵a+b+c=12,
则a+a﹣1+a﹣2=12,
解得:a=5,
则b=a﹣1=4,c=a﹣2=3,
故答案为:5,4,3.
16.解:由题意,设三边分别为3xcm,4xcm,5xcm,
则3x+4x+5x=36,
解得x=3,
三边分别为9cm,12cm,15cm.
故最长的边长比最短的边长长6cm.
故答案是:6cm.
17.解:在△ABC中,∠B=36°,∠C=76°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣36°﹣76°=68°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=×68°=34°.
∵AE是△ABC的高,
∴∠AEC=90°.
在△ACE中,∠AEC=90°,∠C=76°,
∴∠CAE=180°﹣∠AEC﹣∠C=180°﹣90°﹣76°=14°.
∴∠DAE=∠CAD﹣∠CAE=34°﹣14°=20°.
故答案为:20°.
18.解:∵三角形的外角和为360°,
∴∠1+∠2+∠3=360°,
故答案为:360°.
19.解:如图,连接AE并延长交BD于G,连接AF并延长交CD于H,
∵点E、F分别是△ABD和△ACD的重心,
∴DG=BD,DH=CD,AE=2GE,AF=2HF,
∵BC=12,
∴GH=DG+DH=(BD+CD)=BC=×12=6,
∵AE=2GE,AF=2HF,∠EAF=∠GAH,
∴△EAF∽△GAH,
∴==,
∴EF=4,
故答案为:4.
20.解:∵直角三角形的一个内角为40°,
∴这个直角三角形的另一个锐角=90°﹣40°=50°,
故答案为:50°
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
23.解:由题意得,
解得:.
故△ABC的三边长为8cm,
cm,
cm.
24.解:(1)∵∠BED=∠ABE+∠BAD,∠ABE=15°,∠BED=55°,
∴∠BAD=∠BED﹣∠ABE=55°﹣15°=40°.
(2)如图,作EF⊥BC于F,则EF为BD边上的高;
(3)∵AD为△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵BE为△ABD的中线,
∴S△ABE=S△BED=S△ABD,
∵S△ABC=20,
∴S△BED=BD?EF=5,
∵BD=2.5,
∴EF=4
∴△BDE中BD边上的高为4.
25.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
26.解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|a﹣(b+c)|+|b﹣(c+a)|+|c﹣(a+b)|
=b+c﹣a+a+c﹣b+a+b﹣c
=a+b+c.
27.解:∵∠B=42°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=68°,
∵AE是角平分线,
∴∠EAC=∠BAC=34°.
∵AD是高,∠C=70°,
∴∠DAC=90°﹣∠C=20°,
∴∠DAE=∠EAC﹣∠DAC=34°﹣20°=14°,
∠AEC=90°﹣14°=76°.
三角形》单元测试卷
一.选择题
1.如图所示,三角形的个数是( )
A.3
B.4
C.5
D.6
2.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③
B.①②
C.②③
D.①③
3.三角形的重心是三角形三条( )的交点.
A.中线
B.高
C.角平分线
D.垂直平分线
4.三角形按边分类可分为( )
A.不等边三角形、等边三角形
B.等腰三角形、等边三角形
C.不等边三角形、等腰三角形、等边三角形
D.不等边三角形、等腰三角形
5.在三角形ABC中,AB=7,BC=2,并且AC的长为奇数,则AC=( )
A.3
B.5
C.7
D.9
6.如图,在△ABC中,∠B=70°,沿图中虚线EF翻折,使得点B落在AC上的点D处,则∠1+∠2等于( )
A.160°
B.150°
C.140°
D.110°
7.三角形的三个外角的和是( )
A.90°
B.180°
C.270°
D.360°
8.若△ABC中,∠A=90°,且∠B﹣∠C=30°,那么∠C的度数为( )
A.30°
B.40°
C.50°
D.60°
9.如图,称有一条公共边的两个三角形为一对共边三角形,则图中的共边三角形有( )对.
A.8
B.16
C.24
D.32
10.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3
B.
C.
D.6
二.填空题
11.如图,四边形ABCD中,E,F,G,H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为4、5、6,四边形DHOG的面积为
.
12.已知三角形两边长为2和7,则第三边a的取值范围为
.
13.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是
.
14.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是
三角形.
15.三角形周长为12,且三边a,b,c有如下关系,c=b﹣1,b=a﹣1,则a=
,b=
,c=
.
16.三角形的三边之比是3:4:5,周长是36cm,则最长边比最短边长
.
17.如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为
.
18.如图,∠1、∠2、∠3分别是△ABC的3个外角,则∠1+∠2+∠3=
°.
19.如图,点D在△ABC的边BC上,已知点E、点F分别为△ABD和△ADC的重心,如果BC=12,那么两个三角形重心之间的距离EF的长等于
.
20.如果直角三角形的一个内角为40°,则这个直角三角形的另一个锐角为
.
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
23.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
24.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BED=55°,求∠BAD的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为20,BD=2.5,求△BDE中BD边上的高.
25.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
26.已知a、b、c为三角形三边的长,化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|.
27.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
参考答案与试题解析
一.选择题
1.解:如图所示:
三角形有△AED、△BED、△ACD、△ABD、△ABC,共5个.
故选:C.
2.解:①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故选:B.
3.解:三角形的重心是三角形三条中线的交点.
故选:A.
4.解:三角形按边分类可分为不等边三角形、等腰三角形,
故选:D.
5.解:∵AB=7,BC=2,
∴7+2=9,7﹣2=5,
∴5<AC<9,
∵AC为奇数,
∴AC=7.
故选:C.
6.解:∵∠B=70°,
∴∠BEF+∠BFE=110°,
∵翻折,
∴∠BEF=∠DEF,∠BFE=∠DFE,
∴∠BED+∠BFD=2(∠BEF+∠BFE)=2×110°=220°,
∴∠1+∠2=180°×2﹣220°=140°,
故选:C.
7.解:根据三角形外角的性质,可得三角形的三个外角的和是360°.
故选:D.
8.解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B﹣∠C=30°,
∴∠B=60°,∠C=30°,
故选:A.
9.解:以AB为公共边的三角形有:△ABD和△ABC;
以AC为公共边的三角形有:△ACE和△ACB;
以AD为公共边的三角形有:△ADE和△ABD;
以AE为公共边的三角形有:△AED和△AEC;
以BC为公共边的三角形有:△BCO和△BCA和△BCD和△BCE,4个三角形中任何两个都是共边三角形,有6对;
以BD为公共边的三角形有:△BDC,△BDE,BDA任何两个都是3对共边三角形;
以BE为公共边的三角形有:△BEO,△BED,△BEC任何两个都是3对共边三角形.
以OB为公共边的三角形有:△OBE和△OBC;
以CD为公共边的三角形有:△CDO和△CDB和△CDE任何两个都是3对共边三角形.
以CE为公共边的三角形有:△CED,△CEA,△CEB任何两个都是3对共边三角形;
以CO为公共边的三角形有:△COD和△COB;
以DE为公共边的三角形有:△AED和△OED和△BED和三角CED,4个三角形中任何两个都是共边三角形,有6对;
以OD为公共边的三角形有:△ODC和△ODE;
以OE为公共边的三角形有:△OBE和△ODE.
共32对.
故选:D.
10.解:∵S△ABC=BC?hBC=AC?hAC=18,
∴S△ABC=(BD+CD)?hBC=(AE+CE)?hAC=18,
∵AE=CE=AC,S△AEB=AE?hAC,S△BCE=EC?hAC,
∴S△AEB=S△CEB=S△ABC=×18=9,
即S△AEF+S△ABF=9①,
同理:∵BD=2CD,BD+CD=BC,
∴BD=BC,S△ABD=BD?hBC,
∴S△ABD=S△ABC=×18=12,
即S△BDF+S△ABF=12②,
①﹣②得:S△BDF﹣SAEF=(S△BDF+S△ABF)﹣(S△AEF+S△ABF)=12﹣9=3,
故选:A.
二.填空题
11.解:连接OC,OB,OA,OD,
∵E、F、G、H依次是各边中点,
∴△AOE和△BOE等底等高,所以S△OAE=S△OBE,
同理可证,S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,
∵S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,
∴4+6=5+S四边形DHOG,
解得S四边形DHOG=5.
故答案是:5.
12.解:∵7﹣2=5,2+7=9,
∴第三边a的取值范围为5<a<9.
故答案为:5<a<9.
13.解:∵BD是△ABC的中线,
∴AD=CD,
∵△ABD的周长为11,AB=5,BC=3,
∴△BCD的周长是11﹣(5﹣3)=9,
故答案为9.
14.解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
15.解:∵c=b﹣1,b=a﹣1,
∴c=a﹣1﹣1=a﹣2,
又∵a+b+c=12,
则a+a﹣1+a﹣2=12,
解得:a=5,
则b=a﹣1=4,c=a﹣2=3,
故答案为:5,4,3.
16.解:由题意,设三边分别为3xcm,4xcm,5xcm,
则3x+4x+5x=36,
解得x=3,
三边分别为9cm,12cm,15cm.
故最长的边长比最短的边长长6cm.
故答案是:6cm.
17.解:在△ABC中,∠B=36°,∠C=76°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣36°﹣76°=68°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=×68°=34°.
∵AE是△ABC的高,
∴∠AEC=90°.
在△ACE中,∠AEC=90°,∠C=76°,
∴∠CAE=180°﹣∠AEC﹣∠C=180°﹣90°﹣76°=14°.
∴∠DAE=∠CAD﹣∠CAE=34°﹣14°=20°.
故答案为:20°.
18.解:∵三角形的外角和为360°,
∴∠1+∠2+∠3=360°,
故答案为:360°.
19.解:如图,连接AE并延长交BD于G,连接AF并延长交CD于H,
∵点E、F分别是△ABD和△ACD的重心,
∴DG=BD,DH=CD,AE=2GE,AF=2HF,
∵BC=12,
∴GH=DG+DH=(BD+CD)=BC=×12=6,
∵AE=2GE,AF=2HF,∠EAF=∠GAH,
∴△EAF∽△GAH,
∴==,
∴EF=4,
故答案为:4.
20.解:∵直角三角形的一个内角为40°,
∴这个直角三角形的另一个锐角=90°﹣40°=50°,
故答案为:50°
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
23.解:由题意得,
解得:.
故△ABC的三边长为8cm,
cm,
cm.
24.解:(1)∵∠BED=∠ABE+∠BAD,∠ABE=15°,∠BED=55°,
∴∠BAD=∠BED﹣∠ABE=55°﹣15°=40°.
(2)如图,作EF⊥BC于F,则EF为BD边上的高;
(3)∵AD为△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵BE为△ABD的中线,
∴S△ABE=S△BED=S△ABD,
∵S△ABC=20,
∴S△BED=BD?EF=5,
∵BD=2.5,
∴EF=4
∴△BDE中BD边上的高为4.
25.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
26.解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|a﹣(b+c)|+|b﹣(c+a)|+|c﹣(a+b)|
=b+c﹣a+a+c﹣b+a+b﹣c
=a+b+c.
27.解:∵∠B=42°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=68°,
∵AE是角平分线,
∴∠EAC=∠BAC=34°.
∵AD是高,∠C=70°,
∴∠DAC=90°﹣∠C=20°,
∴∠DAE=∠EAC﹣∠DAC=34°﹣20°=14°,
∠AEC=90°﹣14°=76°.
