23.2 中心对称同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级上
23.2中心对称同步练习
一.选择题
1.(2021?夏津县一模)下列图形既是轴对称图形又是中心对称图形的是( )
A.B.
C.
D.
2.(2021春?盐湖区校级期末)如图是一张电子记分牌呈现的数字,其中既是轴对称图形又是中心对称图形的是( )
A.B.
C.
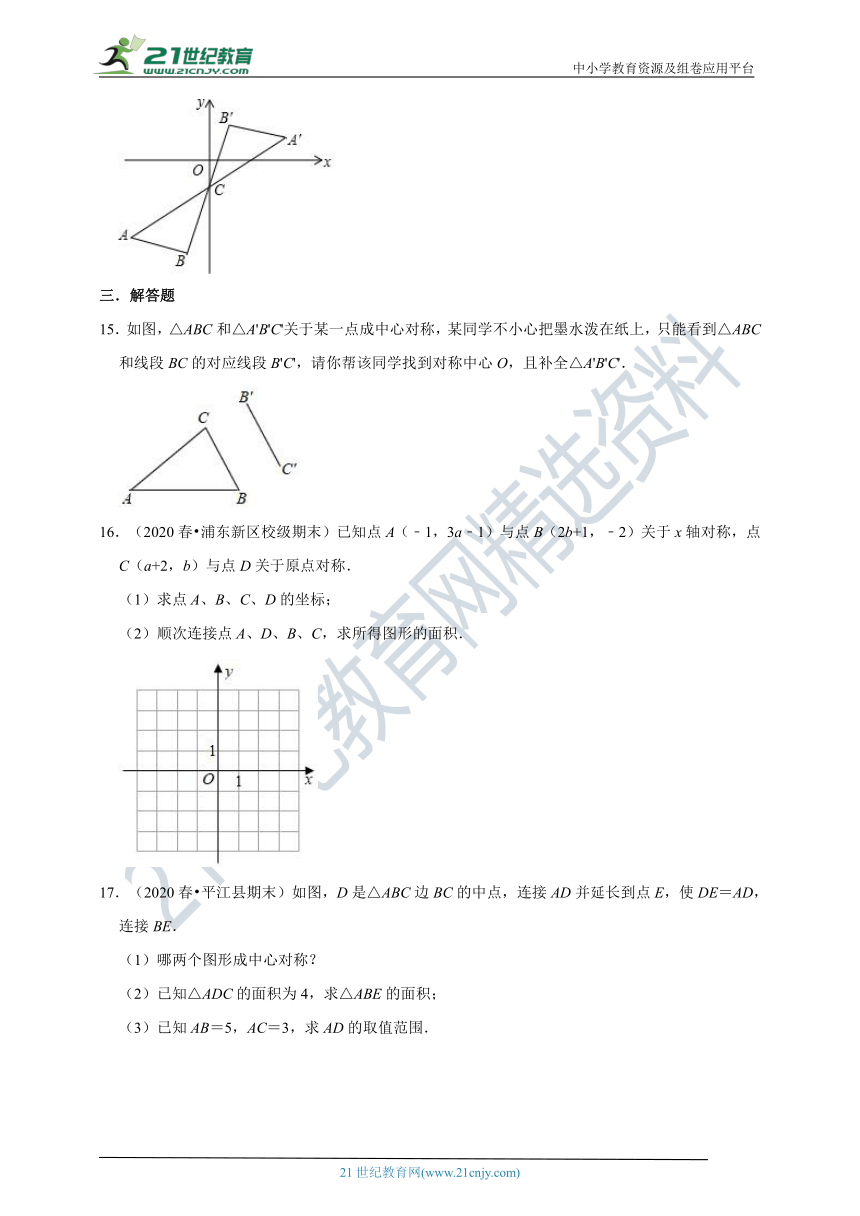
D.
3.(2021春?金台区期末)在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P′的坐标是( )
A.(3,1)
B.(﹣3,﹣1)
C.(﹣3,1)
D.(﹣1,3)
4.(2021春?新乡期末)已知点A(a,﹣1)与点B(3,b)关于原点对称,则a+b的值为( )
A.﹣3
B.﹣2
C.2
D.3
5.(2021春?祁阳县期末)已知A和B两点的坐标分别是(1,3)和(1,﹣3),则( )
A.点A和B关于x轴对称
B.点A和B关于y轴对称
C.点A和B关于原点对称
D.以上说法都不对
6.(2021春?清苑区期末)如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
7.(2021春?兴隆县期末)下列说法错误的是( )
A.平行于x轴的直线上的所有点的纵坐标相同
B.点M(﹣2,1)与(2,﹣1)关于原点成中心对称
C.若点P(a,b)在x轴上,则a=0
D.(﹣3,4)与(4,﹣3)表示两个不同的点
二.填空题
8.(2021春?西安期末)平行四边形
中心对称图形.(填“是”或“不是”)
9.(2021春?鄞州区期中)在直角坐标系中,已知点A(2a,a﹣b+1)和点B(b,a+1)关于原点对称,则ab+ab的值是
.
10.(2021?黄冈一模)在平面直角坐标系中,若点A(x+1,2y+1)与点A'(y﹣2,x)关于原点O对称,则代数式x2﹣y2的值为
.
11.(2020春?舞钢市期末)如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是
.
12.(2021?光明区二模)如图,将△ABC绕边AC的中点O顺时针旋转180°,旋转后的△CDA与△ABC构成四边形ABCD,作ON∥AB交AD于点N,若∠BAC=∠BCA,四边形ABCD的周长为24,则ON=
.
13.(2021春?汝阳县期末)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是
.
14.(2020秋?陆川县期中)如图,将△ABC绕点C(0,﹣1)旋转180°得到△A′B′C,若点A的坐标为(﹣4,﹣3),则点A′的坐标为
.
三.解答题
15.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
16.(2020春?浦东新区校级期末)已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次连接点A、D、B、C,求所得图形的面积.
17.(2020春?平江县期末)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
18.(2019秋?沙坪坝区校级期中)在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时
y=0.
(1)根据已知条件可知这个函数的表达式
.
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点
成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
19.(2019秋?龙岗区期中)如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).
(1)直线y=x﹣经过点C,且与x轴交于点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
20.(2018秋?槐荫区期末)如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
答案与解析
一.选择题
1.(2021?夏津县一模)下列图形既是轴对称图形又是中心对称图形的是( )
A.B.
C.
D.
【解析】解:A.不是轴对称图形,也不是中心对称图形,故本选项不合题意;
B.既是轴对称图形,又是中心对称图形,故本选项符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.不是轴对称图形,是中心对称图形,故本选项不合题意.
故选:B.
2.(2021春?盐湖区校级期末)如图是一张电子记分牌呈现的数字,其中既是轴对称图形又是中心对称图形的是( )
A.B.
C.
D.
【解析】解:A.既不是轴对称图形,也不是中心对称图形.故本选项不合题意;
B.是轴对称图形,不是中心对称图形.故本选项不合题意;
C.既是轴对称图形,又是中心对称图形.故本选项符合题意;
D.不是轴对称图形,是中心对称图形.故本选项不合题意.
故选:C.
3.(2021春?金台区期末)在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P′的坐标是( )
A.(3,1)
B.(﹣3,﹣1)
C.(﹣3,1)
D.(﹣1,3)
【解析】解:点P(3,﹣1)关于坐标原点中心对称的点P′的坐标为(﹣3,1),
故选:C.
4.(2021春?新乡期末)已知点A(a,﹣1)与点B(3,b)关于原点对称,则a+b的值为( )
A.﹣3
B.﹣2
C.2
D.3
【解析】解:∵点A(a,﹣1)与点B(3,b)关于原点对称,
∴a=﹣3,b=1,
∴a+b的值为:﹣3+1=﹣2.
故选:B.
5.(2021春?祁阳县期末)已知A和B两点的坐标分别是(1,3)和(1,﹣3),则( )
A.点A和B关于x轴对称
B.点A和B关于y轴对称
C.点A和B关于原点对称
D.以上说法都不对
【解析】解:∵A和B两点的坐标分别是(1,3)和(1,﹣3),
∴A和B两点的横坐标相同,纵坐标互为相反数,
∴点A和B关于x轴对称.
故选:A.
6.(2021春?清苑区期末)如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
【解析】解:∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对称点,BO=B′O,AB∥A′B′,
故A,B,C正确,
故选:D.
7.(2021春?兴隆县期末)下列说法错误的是( )
A.平行于x轴的直线上的所有点的纵坐标相同
B.点M(﹣2,1)与(2,﹣1)关于原点成中心对称
C.若点P(a,b)在x轴上,则a=0
D.(﹣3,4)与(4,﹣3)表示两个不同的点
【解析】解:A、平行于x轴的直线上的所有点的纵坐标相同,本选项说法正确,不符合题意;
B、点M(﹣2,1)与(2,﹣1)关于原点成中心,本选项说法正确,不符合题意;
C、若点P(a,b)在x轴上,则b=0,本选项说法错误,符合题意;
D、(﹣3,4)与(4,﹣3)表示两个不同的点,本选项说法正确,不符合题意;
故选:C.
二.填空题
8.(2021春?西安期末)平行四边形
是 中心对称图形.(填“是”或“不是”)
【解析】解:平行四边形绕着对角线的交点旋转180°能够与原来的图形重合,故平行四边形是中心对称图形.
故答案为:是.
9.(2021春?鄞州区期中)在直角坐标系中,已知点A(2a,a﹣b+1)和点B(b,a+1)关于原点对称,则ab+ab的值是 ﹣1 .
【解析】解:∵点A(2a,a﹣b+1)和点B(b,a+1)关于原点对称,
∴,
解得:,
则ab+ab的值是:(﹣)1+(﹣)×1=﹣﹣=﹣1.
故答案为:﹣1.
10.(2021?黄冈一模)在平面直角坐标系中,若点A(x+1,2y+1)与点A'(y﹣2,x)关于原点O对称,则代数式x2﹣y2的值为 5 .
【解析】解:∵点A(x+1,2y+1)与点A'(y﹣2,x)关于原点O对称,
∴,
解得:,
故x2﹣y2=9﹣4=5.
故答案为:5.
11.(2020春?舞钢市期末)如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是 .
【解析】解:∵△DEC与△ABC关于点C成中心对称,
∴△ABC≌△DEC,
∴AB=DE=2,AC=DC=1,∠D=∠BAC=90°,
∴AD=2,
∵∠D=90°,
∴AE==2,
故答案为2.
12.(2021?光明区二模)如图,将△ABC绕边AC的中点O顺时针旋转180°,旋转后的△CDA与△ABC构成四边形ABCD,作ON∥AB交AD于点N,若∠BAC=∠BCA,四边形ABCD的周长为24,则ON= 3 .
【解析】解:∵将△ABC绕边AC的中点O顺时针旋转180°得到△CDA,
∴AB=CD,BC=AD,
∵∠BAC=∠BCA,
∴AB=BC,
∴AB=CD=BC=AD,
∴四边形ABCD是菱形,
∴AB∥CD,
∵四边形ABCD的周长为24,
∴CD=6,
∵ON∥AB,
∴ON∥CD,
∵点O是AC的中点,
∴N是AD的中点,
∴ON=CD=3,
故答案为:3.
13.(2021春?汝阳县期末)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 ③ .
【解析】解:当正方形放在③的位置,即是中心对称图形.
故答案为:③.
14.(2020秋?陆川县期中)如图,将△ABC绕点C(0,﹣1)旋转180°得到△A′B′C,若点A的坐标为(﹣4,﹣3),则点A′的坐标为 (4,1) .
【解析】解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,
∵∠A′CE=∠ACD,AC=A′C,
∴△A′EC≌△ADC(AAS),
∴AD=A′E=4,CE=CD,
∵OD=3,OC=1,
∴CD=2,
∴CE=2,
∴OE=1,
∴点A′的坐标为(4,1).
故答案为:(4,1).
三.解答题
15.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
【解析】解:如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
16.(2020春?浦东新区校级期末)已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次连接点A、D、B、C,求所得图形的面积.
【解析】解:(1)∵点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,
∴2b+1=﹣1,3a﹣1=2,
解得a=1,b=﹣1,
∴点A(﹣1,2),B(﹣1,﹣2),C(3,﹣1),
∵点C(a+2,b)与点D关于原点对称,
∴点D(﹣3,1);
(2)如图所示:
四边形ADBC的面积为:.
17.(2020春?平江县期末)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
【解析】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
18.(2019秋?沙坪坝区校级期中)在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时
y=0.
(1)根据已知条件可知这个函数的表达式 y=x3﹣x+2 .
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 (0,2) 成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
【解析】解:(1)由题意:,
解得,
∴函数解析式为y=x3﹣3x+2.
故答案为y=x3﹣3x+2.
(2)函数图象如图所示:
(3)①观察图象可知:函数图象关于(0,2)成中心对称.
故答案为(0,2).
②观察图象可知:当﹣1<x<1时,y随着x的增大而减小.
③观察图象可知:若直线y=c与该图象有3个交点,c的取值范围为0<c<4.
19.(2019秋?龙岗区期中)如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).
(1)直线y=x﹣经过点C,且与x轴交于点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
【解析】解:(1),当y=0时,x=2,
所以E(2,0),
由已知可得:AD=AB=BC=DC=4,AB∥DC,
所以四边形AECD是直角梯形,
所以四边形AECD的面积S=(2﹣1+4)×4÷2=10,
答:四边形AECD的面积是10;
(2)在DC上取一点G,使CG=AE=1,
则S梯形AEGD=S梯形EBCG,易得点G坐标为(4,4),
设直线l的表达式是y=kx+b,
将点E(2,0)代入得:2k+b=0,即b=﹣2k,
将点G(4,4)代入得:4k+b=4,即4k﹣2k=4,
解得k=2,所以b=﹣4,所以y=2x﹣4,
答:直线l的表达式是y=2x﹣4.
20.(2018秋?槐荫区期末)如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
【解析】解:(1)甲图:平行四边形,
(2)乙图:等腰梯形,
(3)丙图:正方形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版九年级上
23.2中心对称同步练习
一.选择题
1.(2021?夏津县一模)下列图形既是轴对称图形又是中心对称图形的是( )
A.B.
C.
D.
2.(2021春?盐湖区校级期末)如图是一张电子记分牌呈现的数字,其中既是轴对称图形又是中心对称图形的是( )
A.B.
C.
D.
3.(2021春?金台区期末)在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P′的坐标是( )
A.(3,1)
B.(﹣3,﹣1)
C.(﹣3,1)
D.(﹣1,3)
4.(2021春?新乡期末)已知点A(a,﹣1)与点B(3,b)关于原点对称,则a+b的值为( )
A.﹣3
B.﹣2
C.2
D.3
5.(2021春?祁阳县期末)已知A和B两点的坐标分别是(1,3)和(1,﹣3),则( )
A.点A和B关于x轴对称
B.点A和B关于y轴对称
C.点A和B关于原点对称
D.以上说法都不对
6.(2021春?清苑区期末)如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
7.(2021春?兴隆县期末)下列说法错误的是( )
A.平行于x轴的直线上的所有点的纵坐标相同
B.点M(﹣2,1)与(2,﹣1)关于原点成中心对称
C.若点P(a,b)在x轴上,则a=0
D.(﹣3,4)与(4,﹣3)表示两个不同的点
二.填空题
8.(2021春?西安期末)平行四边形
中心对称图形.(填“是”或“不是”)
9.(2021春?鄞州区期中)在直角坐标系中,已知点A(2a,a﹣b+1)和点B(b,a+1)关于原点对称,则ab+ab的值是
.
10.(2021?黄冈一模)在平面直角坐标系中,若点A(x+1,2y+1)与点A'(y﹣2,x)关于原点O对称,则代数式x2﹣y2的值为
.
11.(2020春?舞钢市期末)如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是
.
12.(2021?光明区二模)如图,将△ABC绕边AC的中点O顺时针旋转180°,旋转后的△CDA与△ABC构成四边形ABCD,作ON∥AB交AD于点N,若∠BAC=∠BCA,四边形ABCD的周长为24,则ON=
.
13.(2021春?汝阳县期末)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是
.
14.(2020秋?陆川县期中)如图,将△ABC绕点C(0,﹣1)旋转180°得到△A′B′C,若点A的坐标为(﹣4,﹣3),则点A′的坐标为
.
三.解答题
15.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
16.(2020春?浦东新区校级期末)已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次连接点A、D、B、C,求所得图形的面积.
17.(2020春?平江县期末)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
18.(2019秋?沙坪坝区校级期中)在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时
y=0.
(1)根据已知条件可知这个函数的表达式
.
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点
成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
19.(2019秋?龙岗区期中)如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).
(1)直线y=x﹣经过点C,且与x轴交于点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
20.(2018秋?槐荫区期末)如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
答案与解析
一.选择题
1.(2021?夏津县一模)下列图形既是轴对称图形又是中心对称图形的是( )
A.B.
C.
D.
【解析】解:A.不是轴对称图形,也不是中心对称图形,故本选项不合题意;
B.既是轴对称图形,又是中心对称图形,故本选项符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.不是轴对称图形,是中心对称图形,故本选项不合题意.
故选:B.
2.(2021春?盐湖区校级期末)如图是一张电子记分牌呈现的数字,其中既是轴对称图形又是中心对称图形的是( )
A.B.
C.
D.
【解析】解:A.既不是轴对称图形,也不是中心对称图形.故本选项不合题意;
B.是轴对称图形,不是中心对称图形.故本选项不合题意;
C.既是轴对称图形,又是中心对称图形.故本选项符合题意;
D.不是轴对称图形,是中心对称图形.故本选项不合题意.
故选:C.
3.(2021春?金台区期末)在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P′的坐标是( )
A.(3,1)
B.(﹣3,﹣1)
C.(﹣3,1)
D.(﹣1,3)
【解析】解:点P(3,﹣1)关于坐标原点中心对称的点P′的坐标为(﹣3,1),
故选:C.
4.(2021春?新乡期末)已知点A(a,﹣1)与点B(3,b)关于原点对称,则a+b的值为( )
A.﹣3
B.﹣2
C.2
D.3
【解析】解:∵点A(a,﹣1)与点B(3,b)关于原点对称,
∴a=﹣3,b=1,
∴a+b的值为:﹣3+1=﹣2.
故选:B.
5.(2021春?祁阳县期末)已知A和B两点的坐标分别是(1,3)和(1,﹣3),则( )
A.点A和B关于x轴对称
B.点A和B关于y轴对称
C.点A和B关于原点对称
D.以上说法都不对
【解析】解:∵A和B两点的坐标分别是(1,3)和(1,﹣3),
∴A和B两点的横坐标相同,纵坐标互为相反数,
∴点A和B关于x轴对称.
故选:A.
6.(2021春?清苑区期末)如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
【解析】解:∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对称点,BO=B′O,AB∥A′B′,
故A,B,C正确,
故选:D.
7.(2021春?兴隆县期末)下列说法错误的是( )
A.平行于x轴的直线上的所有点的纵坐标相同
B.点M(﹣2,1)与(2,﹣1)关于原点成中心对称
C.若点P(a,b)在x轴上,则a=0
D.(﹣3,4)与(4,﹣3)表示两个不同的点
【解析】解:A、平行于x轴的直线上的所有点的纵坐标相同,本选项说法正确,不符合题意;
B、点M(﹣2,1)与(2,﹣1)关于原点成中心,本选项说法正确,不符合题意;
C、若点P(a,b)在x轴上,则b=0,本选项说法错误,符合题意;
D、(﹣3,4)与(4,﹣3)表示两个不同的点,本选项说法正确,不符合题意;
故选:C.
二.填空题
8.(2021春?西安期末)平行四边形
是 中心对称图形.(填“是”或“不是”)
【解析】解:平行四边形绕着对角线的交点旋转180°能够与原来的图形重合,故平行四边形是中心对称图形.
故答案为:是.
9.(2021春?鄞州区期中)在直角坐标系中,已知点A(2a,a﹣b+1)和点B(b,a+1)关于原点对称,则ab+ab的值是 ﹣1 .
【解析】解:∵点A(2a,a﹣b+1)和点B(b,a+1)关于原点对称,
∴,
解得:,
则ab+ab的值是:(﹣)1+(﹣)×1=﹣﹣=﹣1.
故答案为:﹣1.
10.(2021?黄冈一模)在平面直角坐标系中,若点A(x+1,2y+1)与点A'(y﹣2,x)关于原点O对称,则代数式x2﹣y2的值为 5 .
【解析】解:∵点A(x+1,2y+1)与点A'(y﹣2,x)关于原点O对称,
∴,
解得:,
故x2﹣y2=9﹣4=5.
故答案为:5.
11.(2020春?舞钢市期末)如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是 .
【解析】解:∵△DEC与△ABC关于点C成中心对称,
∴△ABC≌△DEC,
∴AB=DE=2,AC=DC=1,∠D=∠BAC=90°,
∴AD=2,
∵∠D=90°,
∴AE==2,
故答案为2.
12.(2021?光明区二模)如图,将△ABC绕边AC的中点O顺时针旋转180°,旋转后的△CDA与△ABC构成四边形ABCD,作ON∥AB交AD于点N,若∠BAC=∠BCA,四边形ABCD的周长为24,则ON= 3 .
【解析】解:∵将△ABC绕边AC的中点O顺时针旋转180°得到△CDA,
∴AB=CD,BC=AD,
∵∠BAC=∠BCA,
∴AB=BC,
∴AB=CD=BC=AD,
∴四边形ABCD是菱形,
∴AB∥CD,
∵四边形ABCD的周长为24,
∴CD=6,
∵ON∥AB,
∴ON∥CD,
∵点O是AC的中点,
∴N是AD的中点,
∴ON=CD=3,
故答案为:3.
13.(2021春?汝阳县期末)图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 ③ .
【解析】解:当正方形放在③的位置,即是中心对称图形.
故答案为:③.
14.(2020秋?陆川县期中)如图,将△ABC绕点C(0,﹣1)旋转180°得到△A′B′C,若点A的坐标为(﹣4,﹣3),则点A′的坐标为 (4,1) .
【解析】解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,
∵∠A′CE=∠ACD,AC=A′C,
∴△A′EC≌△ADC(AAS),
∴AD=A′E=4,CE=CD,
∵OD=3,OC=1,
∴CD=2,
∴CE=2,
∴OE=1,
∴点A′的坐标为(4,1).
故答案为:(4,1).
三.解答题
15.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
【解析】解:如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
16.(2020春?浦东新区校级期末)已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次连接点A、D、B、C,求所得图形的面积.
【解析】解:(1)∵点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,
∴2b+1=﹣1,3a﹣1=2,
解得a=1,b=﹣1,
∴点A(﹣1,2),B(﹣1,﹣2),C(3,﹣1),
∵点C(a+2,b)与点D关于原点对称,
∴点D(﹣3,1);
(2)如图所示:
四边形ADBC的面积为:.
17.(2020春?平江县期末)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
【解析】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
18.(2019秋?沙坪坝区校级期中)在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时
y=0.
(1)根据已知条件可知这个函数的表达式 y=x3﹣x+2 .
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 (0,2) 成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
【解析】解:(1)由题意:,
解得,
∴函数解析式为y=x3﹣3x+2.
故答案为y=x3﹣3x+2.
(2)函数图象如图所示:
(3)①观察图象可知:函数图象关于(0,2)成中心对称.
故答案为(0,2).
②观察图象可知:当﹣1<x<1时,y随着x的增大而减小.
③观察图象可知:若直线y=c与该图象有3个交点,c的取值范围为0<c<4.
19.(2019秋?龙岗区期中)如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).
(1)直线y=x﹣经过点C,且与x轴交于点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
【解析】解:(1),当y=0时,x=2,
所以E(2,0),
由已知可得:AD=AB=BC=DC=4,AB∥DC,
所以四边形AECD是直角梯形,
所以四边形AECD的面积S=(2﹣1+4)×4÷2=10,
答:四边形AECD的面积是10;
(2)在DC上取一点G,使CG=AE=1,
则S梯形AEGD=S梯形EBCG,易得点G坐标为(4,4),
设直线l的表达式是y=kx+b,
将点E(2,0)代入得:2k+b=0,即b=﹣2k,
将点G(4,4)代入得:4k+b=4,即4k﹣2k=4,
解得k=2,所以b=﹣4,所以y=2x﹣4,
答:直线l的表达式是y=2x﹣4.
20.(2018秋?槐荫区期末)如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
【解析】解:(1)甲图:平行四边形,
(2)乙图:等腰梯形,
(3)丙图:正方形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
