23.3 课题学习 图案设计同步练习(含解析)
文档属性
| 名称 | 23.3 课题学习 图案设计同步练习(含解析) | 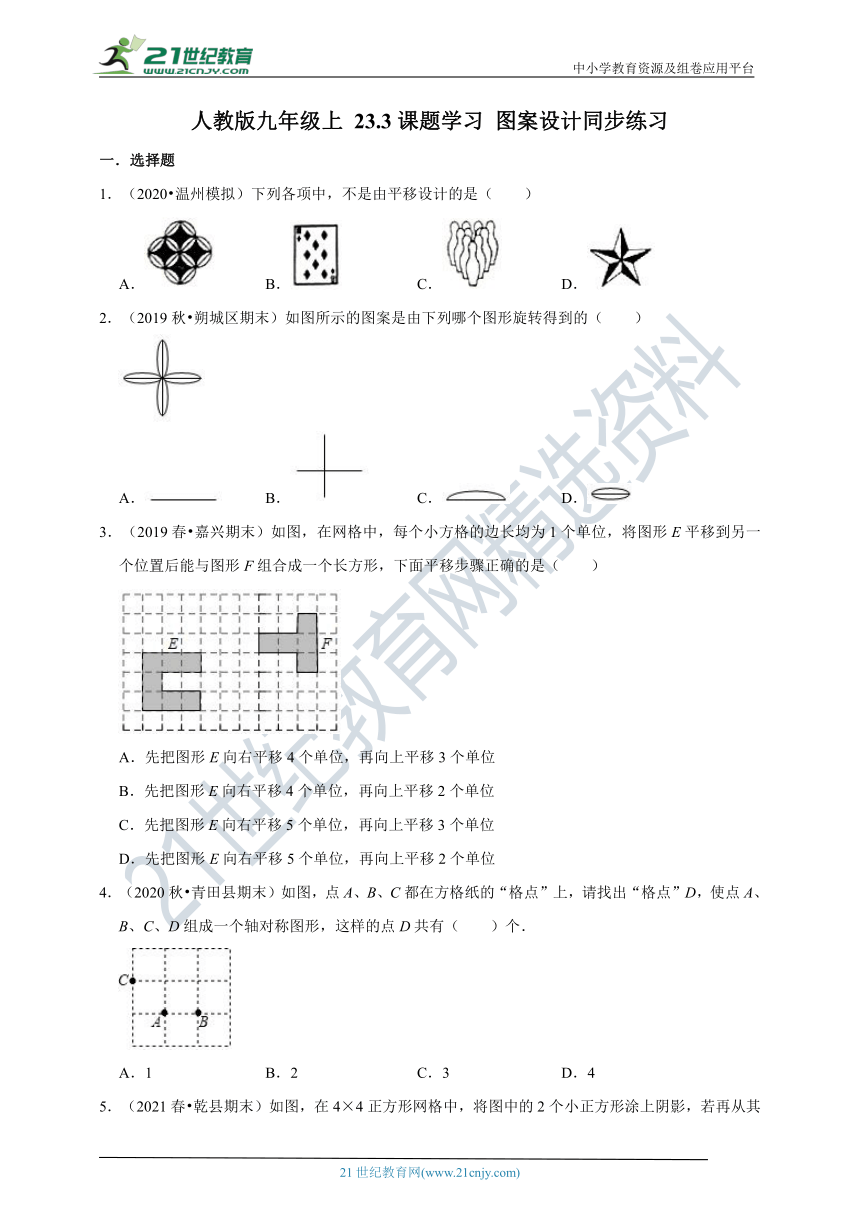 | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:53:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级上
23.3课题学习
图案设计同步练习
一.选择题
1.(2020?温州模拟)下列各项中,不是由平移设计的是( )
A.
B.
C.
D.
2.(2019秋?朔城区期末)如图所示的图案是由下列哪个图形旋转得到的( )
A.
B.
C.
D.
3.(2019春?嘉兴期末)如图,在网格中,每个小方格的边长均为1个单位,将图形E平移到另一个位置后能与图形F组合成一个长方形,下面平移步骤正确的是( )
A.先把图形E向右平移4个单位,再向上平移3个单位
B.先把图形E向右平移4个单位,再向上平移2个单位
C.先把图形E向右平移5个单位,再向上平移3个单位
D.先把图形E向右平移5个单位,再向上平移2个单位
4.(2020秋?青田县期末)如图,点A、B、C都在方格纸的“格点”上,请找出“格点”D,使点A、B、C、D组成一个轴对称图形,这样的点D共有( )个.
A.1
B.2
C.3
D.4
5.(2021春?乾县期末)如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
A.7个
B.8个
C.9个
D.10个
6.(2020秋?台江区期中)在4×4的正方形网格中,从没有涂色的小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( )
A.1个
B.2个
C.3个
D.4个
7.(2020秋?鼓楼区校级月考)如图是由三个小正方形组成的图形,如果在图中补一个同样大小的正方形,使得补后的图形为轴对称图形,这样的补法有( )种.
A.2
B.3
C.4
D.5
8.(2020?江西模拟)如图是由三个全等的菱形拼接成的图形,若平移其中一个菱形,与其他两个菱形重新拼接(无覆盖,有公共顶点),并使拼接成的图形为轴对称图形,则平移的方式共有( )
A.3种
B.6种
C.8种
D.10种
二.填空题
9.(2021春?东坡区校级期末)如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的
.
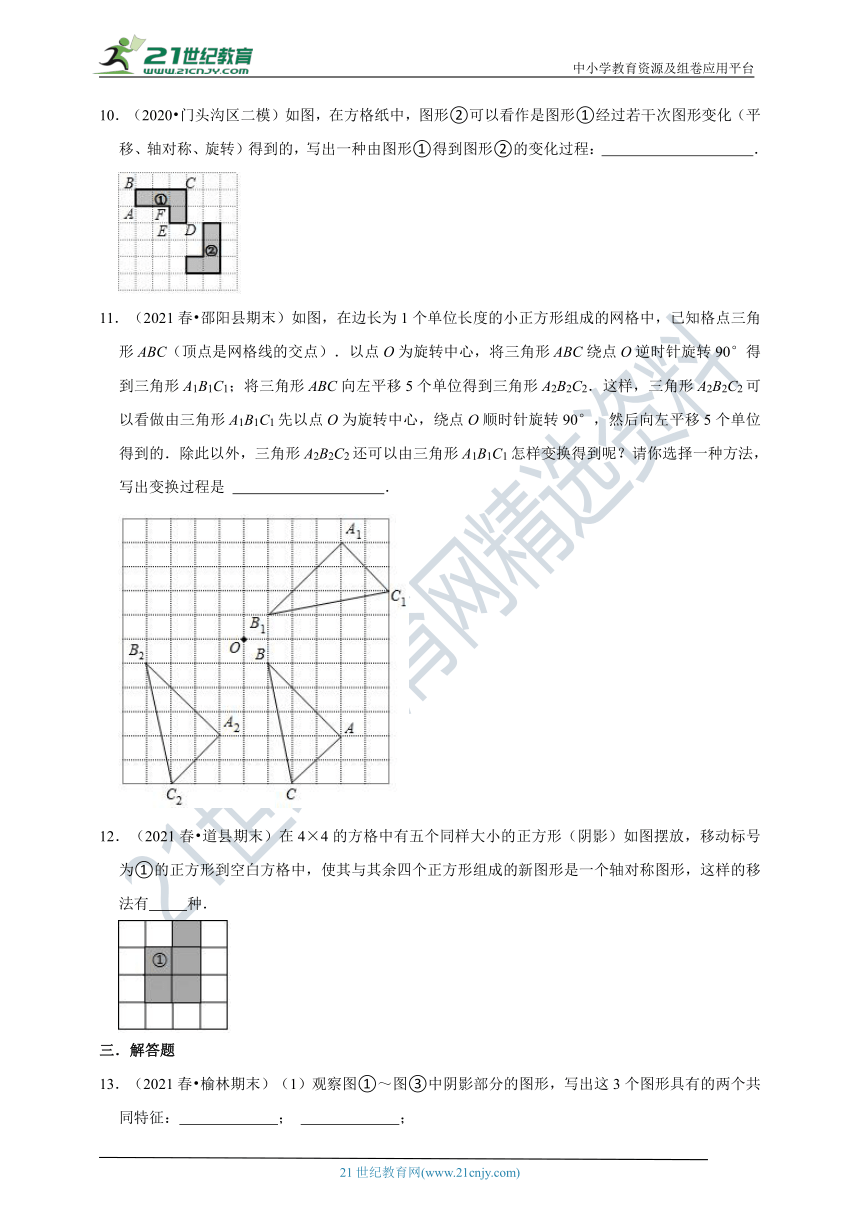
10.(2020?门头沟区二模)如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写出一种由图形①得到图形②的变化过程:
.
11.(2021春?邵阳县期末)如图,在边长为1个单位长度的小正方形组成的网格中,已知格点三角形ABC(顶点是网格线的交点).以点O为旋转中心,将三角形ABC绕点O逆时针旋转90°得到三角形A1B1C1;将三角形ABC向左平移5个单位得到三角形A2B2C2.这样,三角形A2B2C2可以看做由三角形A1B1C1先以点O为旋转中心,绕点O顺时针旋转90°,然后向左平移5个单位得到的.除此以外,三角形A2B2C2还可以由三角形A1B1C1怎样变换得到呢?请你选择一种方法,写出变换过程是
.
12.(2021春?道县期末)在4×4的方格中有五个同样大小的正方形(阴影)如图摆放,移动标号为①的正方形到空白方格中,使其与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有
种.
三.解答题
13.(2021春?榆林期末)(1)观察图①~图③中阴影部分的图形,写出这3个图形具有的两个共同特征:
;
;
(2)在图④、图⑤中设计一个新的图形,使它也具有这两个共同特征.
14.(2021春?郫都区期末)下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.
(1)如图①,整个图形是轴对称图形,画出它的对称轴;
(2)如图②,将某一个方格涂上阴影,使整个图形有两条对称轴;
(3)如图③,将某一个方格涂上阴影,使整个图形有四条对称轴.
15.(2021春?长春期末)图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中,将△ABC沿射线AC向下平移2个单位长度,画出平移后的三角形.
(2)在图②中,画出以BC所在直线为对称轴且与△ABC成轴对称的三角形.
(3)在图③中,将△ABC绕点C顺时针旋转90°,画出旋转后的三角形.
16.(2021春?卧龙区期末)如图,已知四边形ABCD.
(1)画出四边形ABCD向上平移5格后的四边形A1B1C1D1;
(2)画出四边形ABCD关于点O成中心对称的四边形A2B2C2D2;
(3)画出四边形ABCD关于直线MN成轴对称的四边形A3B3C3D3;
(4)四边形A2B2C2D2与四边形A3B3C3D3是否对称?若对称,在图中画出对称轴或对称中心.
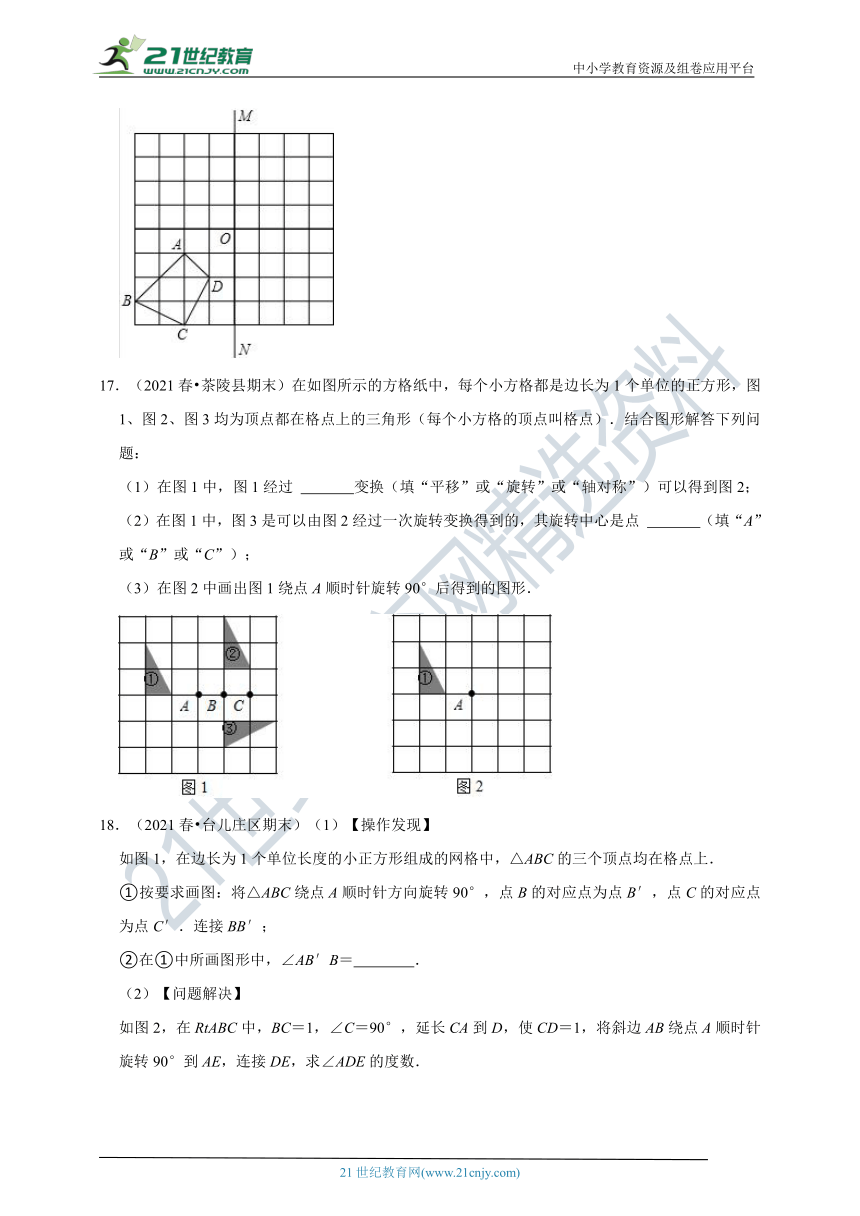
17.(2021春?茶陵县期末)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图1、图2、图3均为顶点都在格点上的三角形(每个小方格的顶点叫格点).结合图形解答下列问题:
(1)在图1中,图1经过
变换(填“平移”或“旋转”或“轴对称”)可以得到图2;
(2)在图1中,图3是可以由图2经过一次旋转变换得到的,其旋转中心是点
(填“A”或“B”或“C”);
(3)在图2中画出图1绕点A顺时针旋转90°后得到的图形.
18.(2021春?台儿庄区期末)(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B=
.
(2)【问题解决】
如图2,在RtABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
答案与解析
一.选择题
1.(2020?温州模拟)下列各项中,不是由平移设计的是( )
A.
B.
C.
D.
【解析】解:根据平移的性质可知:
A、B、C选项的图案都是由平移设计的,
D选项的图案是由旋转设计的.
故选:D.
2.(2019秋?朔城区期末)如图所示的图案是由下列哪个图形旋转得到的( )
A.
B.
C.
D.
【解析】解:由图可得,如图所示的图案是由绕着一端旋转3次,每次旋转90°得到的,
故选:D.
3.(2019春?嘉兴期末)如图,在网格中,每个小方格的边长均为1个单位,将图形E平移到另一个位置后能与图形F组合成一个长方形,下面平移步骤正确的是( )
A.先把图形E向右平移4个单位,再向上平移3个单位
B.先把图形E向右平移4个单位,再向上平移2个单位
C.先把图形E向右平移5个单位,再向上平移3个单位
D.先把图形E向右平移5个单位,再向上平移2个单位
【解析】解:根据网格结构,观察对应点A、A′,点A向右平移5个单位,再向上平移2个单位即可到达点A′的位置,
所以平移步骤是:先把图形E向右平移5个单位,再向上平移2个单位.
故选:D.
4.(2020秋?青田县期末)如图,点A、B、C都在方格纸的“格点”上,请找出“格点”D,使点A、B、C、D组成一个轴对称图形,这样的点D共有( )个.
A.1
B.2
C.3
D.4
【解析】解:如图所示:点A、B、C、D组成一个轴对称图形,这样的点D共有4个.
故选:D.
5.(2021春?乾县期末)如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
A.7个
B.8个
C.9个
D.10个
【解析】解:如图,共有10种符合条件的添法,
故选:D.
6.(2020秋?台江区期中)在4×4的正方形网格中,从没有涂色的小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( )
A.1个
B.2个
C.3个
D.4个
【解析】解:如图所示:将1,2,3位置分别涂上阴影,能使得整个阴影部分组成的图形成轴对称图形.
故选:C.
7.(2020秋?鼓楼区校级月考)如图是由三个小正方形组成的图形,如果在图中补一个同样大小的正方形,使得补后的图形为轴对称图形,这样的补法有( )种.
A.2
B.3
C.4
D.5
【解析】解:补画一个小正方形使补画后的图形为轴对称图形,共有4种补法,如图所示.
故选:C.
8.(2020?江西模拟)如图是由三个全等的菱形拼接成的图形,若平移其中一个菱形,与其他两个菱形重新拼接(无覆盖,有公共顶点),并使拼接成的图形为轴对称图形,则平移的方式共有( )
A.3种
B.6种
C.8种
D.10种
【解析】解:如图,把菱形A平移到①或②或⑤或⑥的位置可得轴对称图形.
把菱形B平移到③或④或⑤或⑥的位置可得轴对称图形.共有8种方法.
故选:C.
二.填空题
9.(2021春?东坡区校级期末)如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的 轴对称变换 .
【解析】解:由图可知,这两个全等三角形属于全等变换中轴对称变换.
故答案为:轴对称变换.
10.(2020?门头沟区二模)如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写出一种由图形①得到图形②的变化过程: 图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形② .
【解析】解:由图形①得到图形②的变化过程:图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形②.
故答案为:图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形②.
11.(2021春?邵阳县期末)如图,在边长为1个单位长度的小正方形组成的网格中,已知格点三角形ABC(顶点是网格线的交点).以点O为旋转中心,将三角形ABC绕点O逆时针旋转90°得到三角形A1B1C1;将三角形ABC向左平移5个单位得到三角形A2B2C2.这样,三角形A2B2C2可以看做由三角形A1B1C1先以点O为旋转中心,绕点O顺时针旋转90°,然后向左平移5个单位得到的.除此以外,三角形A2B2C2还可以由三角形A1B1C1怎样变换得到呢?请你选择一种方法,写出变换过程是
三角形A2B2C2可以看做由三角形A1B1C1先向左平移5个单位得到的,再以点O′为旋转中心,绕点O顺时针旋转90°得到 .
【解析】解:如图,观察图形可知,三角形A2B2C2可以看做由三角形A1B1C1先向左平移5个单位,再以点O′为旋转中心,绕点O顺时针旋转90°得到.
故答案为:三角形A2B2C2可以看做由三角形A1B1C1先向左平移5个单位得到的,再以点O′为旋转中心,绕点O顺时针旋转90°得到.
12.(2021春?道县期末)在4×4的方格中有五个同样大小的正方形(阴影)如图摆放,移动标号为①的正方形到空白方格中,使其与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有 3 种.
【解析】解:如图所示,新图形是一个轴对称图形.
故答案为:3.
三.解答题
13.(2021春?榆林期末)(1)观察图①~图③中阴影部分的图形,写出这3个图形具有的两个共同特征: 阴影部分面积是2 ;
是轴对称图形 ;
(2)在图④、图⑤中设计一个新的图形,使它也具有这两个共同特征.
【解析】解:(1)由图①~图③中阴影部分的图形,则这3个图形具有的两个共同特征:阴影部分面积是2,是轴对称图形;
故答案为:阴影部分面积是2,是轴对称图形;
(2)如图所示:
.
14.(2021春?郫都区期末)下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.
(1)如图①,整个图形是轴对称图形,画出它的对称轴;
(2)如图②,将某一个方格涂上阴影,使整个图形有两条对称轴;
(3)如图③,将某一个方格涂上阴影,使整个图形有四条对称轴.
【解析】解:(1)如图①中,直线m即为所求.
(2)如图②中,图形如图所示.
(3)如图③中,图形如图所示.
15.(2021春?长春期末)图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中,将△ABC沿射线AC向下平移2个单位长度,画出平移后的三角形.
(2)在图②中,画出以BC所在直线为对称轴且与△ABC成轴对称的三角形.
(3)在图③中,将△ABC绕点C顺时针旋转90°,画出旋转后的三角形.
【解析】解:(1)如图①中,△A1B1C1即为所求.
(2)如图②中,△A′BC即为所求.
(3)如图③中,△ECF即为所求.
16.(2021春?卧龙区期末)如图,已知四边形ABCD.
(1)画出四边形ABCD向上平移5格后的四边形A1B1C1D1;
(2)画出四边形ABCD关于点O成中心对称的四边形A2B2C2D2;
(3)画出四边形ABCD关于直线MN成轴对称的四边形A3B3C3D3;
(4)四边形A2B2C2D2与四边形A3B3C3D3是否对称?若对称,在图中画出对称轴或对称中心.
【解析】解:(1)如图所示,四边形A1B1C1D1即为所求;
(2)如图所示,四边形A2B2C2D2即为所求;
(3)如图所示,四边形A3B3C3D3即为所求;
(4)四边形A2B2C2D2与四边形A3B3C3D3成轴对称,如图所示,对称轴为直线l.
17.(2021春?茶陵县期末)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图1、图2、图3均为顶点都在格点上的三角形(每个小方格的顶点叫格点).结合图形解答下列问题:
(1)在图1中,图1经过
平移 变换(填“平移”或“旋转”或“轴对称”)可以得到图2;
(2)在图1中,图3是可以由图2经过一次旋转变换得到的,其旋转中心是点
A (填“A”或“B”或“C”);
(3)在图2中画出图1绕点A顺时针旋转90°后得到的图形.
【解析】解:(1)图1经过平移变换可以得到图2,
故答案为:平移.
(2)图3是可以由图2经过一次旋转变换得到的,其旋转中心是点A.
故答案为:A.
(3)如图,旋转后的图形如图所示.
18.(2021春?台儿庄区期末)(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B= 45° .
(2)【问题解决】
如图2,在RtABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
【解析】解:(1)①如图1,
②∵△ABC绕点A顺时针方向旋转90°得到△AB′C′,
∴AB=AB′,∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴∠AB′B=45°;
故答案为45°;
(2)在CB上截取CF=CA,如图2,
∵∠C=90°,
∴△CAF为等腰直角三角形,
∴∠CAF=∠CFA=45°,
∴∠BFA=135°,∠B+∠BAF=45°,
∵CB=CD,
即CF+BF=CA+AD,
∴BF=AD,
∵AB绕点A顺时针旋转90°到AE,
∴AB=AE,∠BAE=90°,
∴∠BAF+∠DAE=45°,
∴∠B=∠DAE,
在△ADE和△BFA中,
,
∴△ADE≌△BFA(SAS),
∴∠ADE=∠BFA=135°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版九年级上
23.3课题学习
图案设计同步练习
一.选择题
1.(2020?温州模拟)下列各项中,不是由平移设计的是( )
A.
B.
C.
D.
2.(2019秋?朔城区期末)如图所示的图案是由下列哪个图形旋转得到的( )
A.
B.
C.
D.
3.(2019春?嘉兴期末)如图,在网格中,每个小方格的边长均为1个单位,将图形E平移到另一个位置后能与图形F组合成一个长方形,下面平移步骤正确的是( )
A.先把图形E向右平移4个单位,再向上平移3个单位
B.先把图形E向右平移4个单位,再向上平移2个单位
C.先把图形E向右平移5个单位,再向上平移3个单位
D.先把图形E向右平移5个单位,再向上平移2个单位
4.(2020秋?青田县期末)如图,点A、B、C都在方格纸的“格点”上,请找出“格点”D,使点A、B、C、D组成一个轴对称图形,这样的点D共有( )个.
A.1
B.2
C.3
D.4
5.(2021春?乾县期末)如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
A.7个
B.8个
C.9个
D.10个
6.(2020秋?台江区期中)在4×4的正方形网格中,从没有涂色的小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( )
A.1个
B.2个
C.3个
D.4个
7.(2020秋?鼓楼区校级月考)如图是由三个小正方形组成的图形,如果在图中补一个同样大小的正方形,使得补后的图形为轴对称图形,这样的补法有( )种.
A.2
B.3
C.4
D.5
8.(2020?江西模拟)如图是由三个全等的菱形拼接成的图形,若平移其中一个菱形,与其他两个菱形重新拼接(无覆盖,有公共顶点),并使拼接成的图形为轴对称图形,则平移的方式共有( )
A.3种
B.6种
C.8种
D.10种
二.填空题
9.(2021春?东坡区校级期末)如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的
.
10.(2020?门头沟区二模)如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写出一种由图形①得到图形②的变化过程:
.
11.(2021春?邵阳县期末)如图,在边长为1个单位长度的小正方形组成的网格中,已知格点三角形ABC(顶点是网格线的交点).以点O为旋转中心,将三角形ABC绕点O逆时针旋转90°得到三角形A1B1C1;将三角形ABC向左平移5个单位得到三角形A2B2C2.这样,三角形A2B2C2可以看做由三角形A1B1C1先以点O为旋转中心,绕点O顺时针旋转90°,然后向左平移5个单位得到的.除此以外,三角形A2B2C2还可以由三角形A1B1C1怎样变换得到呢?请你选择一种方法,写出变换过程是
.
12.(2021春?道县期末)在4×4的方格中有五个同样大小的正方形(阴影)如图摆放,移动标号为①的正方形到空白方格中,使其与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有
种.
三.解答题
13.(2021春?榆林期末)(1)观察图①~图③中阴影部分的图形,写出这3个图形具有的两个共同特征:
;
;
(2)在图④、图⑤中设计一个新的图形,使它也具有这两个共同特征.
14.(2021春?郫都区期末)下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.
(1)如图①,整个图形是轴对称图形,画出它的对称轴;
(2)如图②,将某一个方格涂上阴影,使整个图形有两条对称轴;
(3)如图③,将某一个方格涂上阴影,使整个图形有四条对称轴.
15.(2021春?长春期末)图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中,将△ABC沿射线AC向下平移2个单位长度,画出平移后的三角形.
(2)在图②中,画出以BC所在直线为对称轴且与△ABC成轴对称的三角形.
(3)在图③中,将△ABC绕点C顺时针旋转90°,画出旋转后的三角形.
16.(2021春?卧龙区期末)如图,已知四边形ABCD.
(1)画出四边形ABCD向上平移5格后的四边形A1B1C1D1;
(2)画出四边形ABCD关于点O成中心对称的四边形A2B2C2D2;
(3)画出四边形ABCD关于直线MN成轴对称的四边形A3B3C3D3;
(4)四边形A2B2C2D2与四边形A3B3C3D3是否对称?若对称,在图中画出对称轴或对称中心.
17.(2021春?茶陵县期末)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图1、图2、图3均为顶点都在格点上的三角形(每个小方格的顶点叫格点).结合图形解答下列问题:
(1)在图1中,图1经过
变换(填“平移”或“旋转”或“轴对称”)可以得到图2;
(2)在图1中,图3是可以由图2经过一次旋转变换得到的,其旋转中心是点
(填“A”或“B”或“C”);
(3)在图2中画出图1绕点A顺时针旋转90°后得到的图形.
18.(2021春?台儿庄区期末)(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B=
.
(2)【问题解决】
如图2,在RtABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
答案与解析
一.选择题
1.(2020?温州模拟)下列各项中,不是由平移设计的是( )
A.
B.
C.
D.
【解析】解:根据平移的性质可知:
A、B、C选项的图案都是由平移设计的,
D选项的图案是由旋转设计的.
故选:D.
2.(2019秋?朔城区期末)如图所示的图案是由下列哪个图形旋转得到的( )
A.
B.
C.
D.
【解析】解:由图可得,如图所示的图案是由绕着一端旋转3次,每次旋转90°得到的,
故选:D.
3.(2019春?嘉兴期末)如图,在网格中,每个小方格的边长均为1个单位,将图形E平移到另一个位置后能与图形F组合成一个长方形,下面平移步骤正确的是( )
A.先把图形E向右平移4个单位,再向上平移3个单位
B.先把图形E向右平移4个单位,再向上平移2个单位
C.先把图形E向右平移5个单位,再向上平移3个单位
D.先把图形E向右平移5个单位,再向上平移2个单位
【解析】解:根据网格结构,观察对应点A、A′,点A向右平移5个单位,再向上平移2个单位即可到达点A′的位置,
所以平移步骤是:先把图形E向右平移5个单位,再向上平移2个单位.
故选:D.
4.(2020秋?青田县期末)如图,点A、B、C都在方格纸的“格点”上,请找出“格点”D,使点A、B、C、D组成一个轴对称图形,这样的点D共有( )个.
A.1
B.2
C.3
D.4
【解析】解:如图所示:点A、B、C、D组成一个轴对称图形,这样的点D共有4个.
故选:D.
5.(2021春?乾县期末)如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
A.7个
B.8个
C.9个
D.10个
【解析】解:如图,共有10种符合条件的添法,
故选:D.
6.(2020秋?台江区期中)在4×4的正方形网格中,从没有涂色的小正方形中任选一个涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( )
A.1个
B.2个
C.3个
D.4个
【解析】解:如图所示:将1,2,3位置分别涂上阴影,能使得整个阴影部分组成的图形成轴对称图形.
故选:C.
7.(2020秋?鼓楼区校级月考)如图是由三个小正方形组成的图形,如果在图中补一个同样大小的正方形,使得补后的图形为轴对称图形,这样的补法有( )种.
A.2
B.3
C.4
D.5
【解析】解:补画一个小正方形使补画后的图形为轴对称图形,共有4种补法,如图所示.
故选:C.
8.(2020?江西模拟)如图是由三个全等的菱形拼接成的图形,若平移其中一个菱形,与其他两个菱形重新拼接(无覆盖,有公共顶点),并使拼接成的图形为轴对称图形,则平移的方式共有( )
A.3种
B.6种
C.8种
D.10种
【解析】解:如图,把菱形A平移到①或②或⑤或⑥的位置可得轴对称图形.
把菱形B平移到③或④或⑤或⑥的位置可得轴对称图形.共有8种方法.
故选:C.
二.填空题
9.(2021春?东坡区校级期末)如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的 轴对称变换 .
【解析】解:由图可知,这两个全等三角形属于全等变换中轴对称变换.
故答案为:轴对称变换.
10.(2020?门头沟区二模)如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写出一种由图形①得到图形②的变化过程: 图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形② .
【解析】解:由图形①得到图形②的变化过程:图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形②.
故答案为:图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形②.
11.(2021春?邵阳县期末)如图,在边长为1个单位长度的小正方形组成的网格中,已知格点三角形ABC(顶点是网格线的交点).以点O为旋转中心,将三角形ABC绕点O逆时针旋转90°得到三角形A1B1C1;将三角形ABC向左平移5个单位得到三角形A2B2C2.这样,三角形A2B2C2可以看做由三角形A1B1C1先以点O为旋转中心,绕点O顺时针旋转90°,然后向左平移5个单位得到的.除此以外,三角形A2B2C2还可以由三角形A1B1C1怎样变换得到呢?请你选择一种方法,写出变换过程是
三角形A2B2C2可以看做由三角形A1B1C1先向左平移5个单位得到的,再以点O′为旋转中心,绕点O顺时针旋转90°得到 .
【解析】解:如图,观察图形可知,三角形A2B2C2可以看做由三角形A1B1C1先向左平移5个单位,再以点O′为旋转中心,绕点O顺时针旋转90°得到.
故答案为:三角形A2B2C2可以看做由三角形A1B1C1先向左平移5个单位得到的,再以点O′为旋转中心,绕点O顺时针旋转90°得到.
12.(2021春?道县期末)在4×4的方格中有五个同样大小的正方形(阴影)如图摆放,移动标号为①的正方形到空白方格中,使其与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有 3 种.
【解析】解:如图所示,新图形是一个轴对称图形.
故答案为:3.
三.解答题
13.(2021春?榆林期末)(1)观察图①~图③中阴影部分的图形,写出这3个图形具有的两个共同特征: 阴影部分面积是2 ;
是轴对称图形 ;
(2)在图④、图⑤中设计一个新的图形,使它也具有这两个共同特征.
【解析】解:(1)由图①~图③中阴影部分的图形,则这3个图形具有的两个共同特征:阴影部分面积是2,是轴对称图形;
故答案为:阴影部分面积是2,是轴对称图形;
(2)如图所示:
.
14.(2021春?郫都区期末)下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.
(1)如图①,整个图形是轴对称图形,画出它的对称轴;
(2)如图②,将某一个方格涂上阴影,使整个图形有两条对称轴;
(3)如图③,将某一个方格涂上阴影,使整个图形有四条对称轴.
【解析】解:(1)如图①中,直线m即为所求.
(2)如图②中,图形如图所示.
(3)如图③中,图形如图所示.
15.(2021春?长春期末)图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中,将△ABC沿射线AC向下平移2个单位长度,画出平移后的三角形.
(2)在图②中,画出以BC所在直线为对称轴且与△ABC成轴对称的三角形.
(3)在图③中,将△ABC绕点C顺时针旋转90°,画出旋转后的三角形.
【解析】解:(1)如图①中,△A1B1C1即为所求.
(2)如图②中,△A′BC即为所求.
(3)如图③中,△ECF即为所求.
16.(2021春?卧龙区期末)如图,已知四边形ABCD.
(1)画出四边形ABCD向上平移5格后的四边形A1B1C1D1;
(2)画出四边形ABCD关于点O成中心对称的四边形A2B2C2D2;
(3)画出四边形ABCD关于直线MN成轴对称的四边形A3B3C3D3;
(4)四边形A2B2C2D2与四边形A3B3C3D3是否对称?若对称,在图中画出对称轴或对称中心.
【解析】解:(1)如图所示,四边形A1B1C1D1即为所求;
(2)如图所示,四边形A2B2C2D2即为所求;
(3)如图所示,四边形A3B3C3D3即为所求;
(4)四边形A2B2C2D2与四边形A3B3C3D3成轴对称,如图所示,对称轴为直线l.
17.(2021春?茶陵县期末)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图1、图2、图3均为顶点都在格点上的三角形(每个小方格的顶点叫格点).结合图形解答下列问题:
(1)在图1中,图1经过
平移 变换(填“平移”或“旋转”或“轴对称”)可以得到图2;
(2)在图1中,图3是可以由图2经过一次旋转变换得到的,其旋转中心是点
A (填“A”或“B”或“C”);
(3)在图2中画出图1绕点A顺时针旋转90°后得到的图形.
【解析】解:(1)图1经过平移变换可以得到图2,
故答案为:平移.
(2)图3是可以由图2经过一次旋转变换得到的,其旋转中心是点A.
故答案为:A.
(3)如图,旋转后的图形如图所示.
18.(2021春?台儿庄区期末)(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B= 45° .
(2)【问题解决】
如图2,在RtABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
【解析】解:(1)①如图1,
②∵△ABC绕点A顺时针方向旋转90°得到△AB′C′,
∴AB=AB′,∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴∠AB′B=45°;
故答案为45°;
(2)在CB上截取CF=CA,如图2,
∵∠C=90°,
∴△CAF为等腰直角三角形,
∴∠CAF=∠CFA=45°,
∴∠BFA=135°,∠B+∠BAF=45°,
∵CB=CD,
即CF+BF=CA+AD,
∴BF=AD,
∵AB绕点A顺时针旋转90°到AE,
∴AB=AE,∠BAE=90°,
∴∠BAF+∠DAE=45°,
∴∠B=∠DAE,
在△ADE和△BFA中,
,
∴△ADE≌△BFA(SAS),
∴∠ADE=∠BFA=135°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
