西藏山南市高中2020-2021学年高一下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 西藏山南市高中2020-2021学年高一下学期期末考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 773.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:48:49 | ||
图片预览




文档简介
____________________________________________________________________________________________
山南市高中
2020-2021学年高一第二学期期末考试试卷
数学
注意事项:
1、本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分为:150分,考试时间为:120分钟.
2、答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上;写在本试卷上无效。
4、考试结束后,监考人员将答题卡收回。
第I卷(选择题)
一、单选题(共60分)
1
.已知集合,集合,则(
)
A.
B.
C.
D.
2.在一次抛硬币的试验中,某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,那么出现正面朝上的频率和概率分别为(
)
A.
B.
C.
D.
3.
已知扇形的周长是,面积是,则扇形的中心角的弧度数是
A.
B.
C.或
D.或
4.
已知向量,,,,∥,则的值为(
)
A.
B.3
C.
D.
5.
.函数(,,)的图象关于直线对称,它的最小正周期为,则函数图象的一个对称中心是(
)
A.
B.
C.
D.
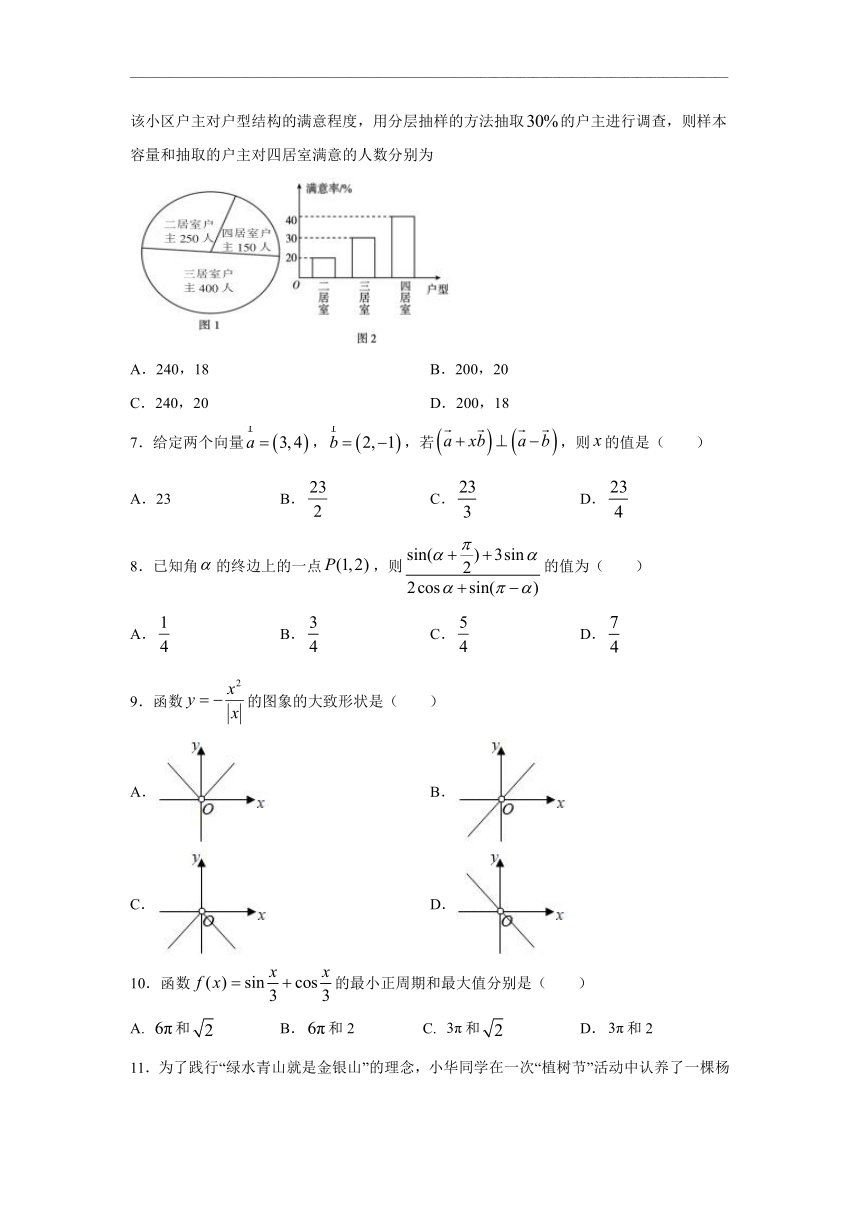
6.已知我市某居民小区户主人数和户主对户型结构的满意率分别如图和如图所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为
A.240,18
B.200,20
C.240,20
D.200,18
7.给定两个向量,,若,则的值是(
)
A.23
B.
C.
D.
8.已知角的终边上的一点,则的值为(
)
A.
B.
C.
D.
9.函数的图象的大致形状是(
)
A.
B.
C.
D.
10.函数的最小正周期和最大值分别是(
)
A.
和
B.和2
C.
和
D.和2
11.为了践行“绿水青山就是金银山”的理念,小华同学在一次“植树节”活动中认养了一棵杨树.据统计,杨树的生长年份和高度的统计数据如表.
年份
3
4
5
6
高度
250
300
400
450
由散点图可以看出,具有线性相关关系,并求得回归方程为.据此模型估计,该杨树生长8年后的高度为(
)
A.
B.
C.
D.
12已知,则的终边在(
)
A.第一象限
B.第二象限
C.三象限
D.第四象限
第II卷(非选择题)
二、填空题(共20分)
13.函数的定义域为__________、最小正周期为__________.
14.
的值为_________.
15.
已知,,,则在方向上的投影等于__________.
16.函数的图象可由函数的图象至少向左平移__________个单位长度得到.
三、解答题(共5*14=70分)
17.已知平面内两个不共线的向量,.
(1)求;
(2)求与的夹角.
18.已知,均为锐角,且,.
(1)求的值;
(2)求的值.
19.已知点A、B、C的坐标分别为、、,.
(1)若,求角的值;
(2)若,求的值.
20.某校两个班级100名学生在一次考试中的成绩的频率分布直方图如图所示,其中成绩分组区如下表:
组号
第一组
第二组
第三组
第四组
第五组
分组
(1)求频率表分布直方图中a的值;
(2)根据频率表分布直方图,估计这100名学生这次考试成绩的平均分;
(3)现用分层抽样的方法从第三、四、五组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
21.已知函数(),再从条件①的最大值为2;条件②.中选择一个作为已知,求:
(1)的值;
(2)将的图象向右平移个单位得到的图象,求函数的单调增区间.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
参考答案
1.
B
【详解】
解:因为或,
所以,
所以
2.
A
【详解】
100次试验中有40次正面朝上,所以正面朝上的频率为,
因为硬币质地均匀,所以正面朝上和反面朝上的概率都是0.5.
3.C
【详解】
设扇形的半径为,弧长为
,则
∴解得
或
4.D
【详解】
由∥,得,即.
5.
B
【详解】
由,解得,
可得,
再由函数图象关于直线对称,
故,故可取,
故函数,
令,,
可得,,故函数的对称中心为,,
令,可得函数图象的一个对称中心为.
6.A
【详解】
样本容量为:(150+250+400)×30%=240,
∴抽取的户主对四居室满意的人数为:
7.C
【详解】
,
,
又,
即,
整理得,解得,
8.D
又因为角的终边上的一点,所以,
所以.
9.C
【详解】
解:方法一:
方法二:,故图像全部在轴下方
10.A
【详解】
由题,所以的最小正周期为,最大值为.
11.A
【详解】
解:,,
所以就有,解得:,
所以杨树生长8年后的高度为,
12.D
【详解】
解:由,平方得:,则,即,则或,,即有或,,
当为偶数时,位于第二象限,,,,不成立,
当为奇数时,位于第四象限,,,成立.
∴角的终边在第四象限.
13.【详解】
令,则由得,
即函数的定义域是
最小正周期为
14.
【详解】
.
15.
【详解】
设的夹角为,,
,
解得:,
则在方向上的投影为.
16.
【解析】,将向左平移得到的图像.
17.(1)2;(2).
【详解】
解:(1),
,
;
(2),
,且,
与的夹角为.
18.(1);(2).
【详解】
(1)由,均为锐角,
可得在第四象限,
则,
所以;
(2)由,
得,
.
19.(1)a=0.005;(2)74.5;(3)
【详解】
(1)由题意得10a+0.01×10+0.02×10+0.03×10+0.035×10=1,所以a=0.005.
(2)由直方图分数在[50,60]的频率为0.05,[60,70]的频率为0.35,[70,80]的频率为0.30,[80,90]的频率为0.20,[90,100]的频率为0.10,所以这100名学生期中考试数学成绩的平均分的估计值为:55×0.05+65×0.35+75×0.30+85×0.20+95×0.10=74.5
(3)由直方图,得:
第3组人数为0.3×100=30,
第4组人数为0.2×100=20人,
第5组人数为0.1×100=10人.
所以利用分层抽样在60名学生中抽取6名学生,
每组分别为:
第3组:人,
第4组:人,
第5组:=1人.
所以第3、4、5组分别抽取3人、2人、1人.
设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,则从六位同学中抽两位同学有15种可能如下:
(A1,A2),(A1,A3),(A2,A3),(B1,B2),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A1,C1),(A2,C1),(A3,C1),(B1,C1),(B2,C1),其中恰有1人的分数不低于90(分)的情形有:(A1,C1),(A2,C1),(A3,C1),(B1,C1),(B2,C1),共5种.
所以恰有1人的分数不低于90分的概率为.
20.(1);(2)
【详解】
(1)∵,
∴化简得,
∵,∴.
(2)∵,
∴,
∴,∴,
∴.
21.选择见解析;(1);(2)单调增区间为.
【详解】
解:(1)选择①:因为
所以,其中,
所以,又因为,所以.
选择②:,所以.
(2)因为
所以
则,
,
所以函数的单调增区间为
(一个都没写的扣一分)
山南市高中
2020-2021学年高一第二学期期末考试试卷
数学
注意事项:
1、本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分为:150分,考试时间为:120分钟.
2、答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上;写在本试卷上无效。
4、考试结束后,监考人员将答题卡收回。
第I卷(选择题)
一、单选题(共60分)
1
.已知集合,集合,则(
)
A.
B.
C.
D.
2.在一次抛硬币的试验中,某同学用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了40次,那么出现正面朝上的频率和概率分别为(
)
A.
B.
C.
D.
3.
已知扇形的周长是,面积是,则扇形的中心角的弧度数是
A.
B.
C.或
D.或
4.
已知向量,,,,∥,则的值为(
)
A.
B.3
C.
D.
5.
.函数(,,)的图象关于直线对称,它的最小正周期为,则函数图象的一个对称中心是(
)
A.
B.
C.
D.
6.已知我市某居民小区户主人数和户主对户型结构的满意率分别如图和如图所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为
A.240,18
B.200,20
C.240,20
D.200,18
7.给定两个向量,,若,则的值是(
)
A.23
B.
C.
D.
8.已知角的终边上的一点,则的值为(
)
A.
B.
C.
D.
9.函数的图象的大致形状是(
)
A.
B.
C.
D.
10.函数的最小正周期和最大值分别是(
)
A.
和
B.和2
C.
和
D.和2
11.为了践行“绿水青山就是金银山”的理念,小华同学在一次“植树节”活动中认养了一棵杨树.据统计,杨树的生长年份和高度的统计数据如表.
年份
3
4
5
6
高度
250
300
400
450
由散点图可以看出,具有线性相关关系,并求得回归方程为.据此模型估计,该杨树生长8年后的高度为(
)
A.
B.
C.
D.
12已知,则的终边在(
)
A.第一象限
B.第二象限
C.三象限
D.第四象限
第II卷(非选择题)
二、填空题(共20分)
13.函数的定义域为__________、最小正周期为__________.
14.
的值为_________.
15.
已知,,,则在方向上的投影等于__________.
16.函数的图象可由函数的图象至少向左平移__________个单位长度得到.
三、解答题(共5*14=70分)
17.已知平面内两个不共线的向量,.
(1)求;
(2)求与的夹角.
18.已知,均为锐角,且,.
(1)求的值;
(2)求的值.
19.已知点A、B、C的坐标分别为、、,.
(1)若,求角的值;
(2)若,求的值.
20.某校两个班级100名学生在一次考试中的成绩的频率分布直方图如图所示,其中成绩分组区如下表:
组号
第一组
第二组
第三组
第四组
第五组
分组
(1)求频率表分布直方图中a的值;
(2)根据频率表分布直方图,估计这100名学生这次考试成绩的平均分;
(3)现用分层抽样的方法从第三、四、五组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
21.已知函数(),再从条件①的最大值为2;条件②.中选择一个作为已知,求:
(1)的值;
(2)将的图象向右平移个单位得到的图象,求函数的单调增区间.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
参考答案
1.
B
【详解】
解:因为或,
所以,
所以
2.
A
【详解】
100次试验中有40次正面朝上,所以正面朝上的频率为,
因为硬币质地均匀,所以正面朝上和反面朝上的概率都是0.5.
3.C
【详解】
设扇形的半径为,弧长为
,则
∴解得
或
4.D
【详解】
由∥,得,即.
5.
B
【详解】
由,解得,
可得,
再由函数图象关于直线对称,
故,故可取,
故函数,
令,,
可得,,故函数的对称中心为,,
令,可得函数图象的一个对称中心为.
6.A
【详解】
样本容量为:(150+250+400)×30%=240,
∴抽取的户主对四居室满意的人数为:
7.C
【详解】
,
,
又,
即,
整理得,解得,
8.D
又因为角的终边上的一点,所以,
所以.
9.C
【详解】
解:方法一:
方法二:,故图像全部在轴下方
10.A
【详解】
由题,所以的最小正周期为,最大值为.
11.A
【详解】
解:,,
所以就有,解得:,
所以杨树生长8年后的高度为,
12.D
【详解】
解:由,平方得:,则,即,则或,,即有或,,
当为偶数时,位于第二象限,,,,不成立,
当为奇数时,位于第四象限,,,成立.
∴角的终边在第四象限.
13.【详解】
令,则由得,
即函数的定义域是
最小正周期为
14.
【详解】
.
15.
【详解】
设的夹角为,,
,
解得:,
则在方向上的投影为.
16.
【解析】,将向左平移得到的图像.
17.(1)2;(2).
【详解】
解:(1),
,
;
(2),
,且,
与的夹角为.
18.(1);(2).
【详解】
(1)由,均为锐角,
可得在第四象限,
则,
所以;
(2)由,
得,
.
19.(1)a=0.005;(2)74.5;(3)
【详解】
(1)由题意得10a+0.01×10+0.02×10+0.03×10+0.035×10=1,所以a=0.005.
(2)由直方图分数在[50,60]的频率为0.05,[60,70]的频率为0.35,[70,80]的频率为0.30,[80,90]的频率为0.20,[90,100]的频率为0.10,所以这100名学生期中考试数学成绩的平均分的估计值为:55×0.05+65×0.35+75×0.30+85×0.20+95×0.10=74.5
(3)由直方图,得:
第3组人数为0.3×100=30,
第4组人数为0.2×100=20人,
第5组人数为0.1×100=10人.
所以利用分层抽样在60名学生中抽取6名学生,
每组分别为:
第3组:人,
第4组:人,
第5组:=1人.
所以第3、4、5组分别抽取3人、2人、1人.
设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,则从六位同学中抽两位同学有15种可能如下:
(A1,A2),(A1,A3),(A2,A3),(B1,B2),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A1,C1),(A2,C1),(A3,C1),(B1,C1),(B2,C1),其中恰有1人的分数不低于90(分)的情形有:(A1,C1),(A2,C1),(A3,C1),(B1,C1),(B2,C1),共5种.
所以恰有1人的分数不低于90分的概率为.
20.(1);(2)
【详解】
(1)∵,
∴化简得,
∵,∴.
(2)∵,
∴,
∴,∴,
∴.
21.选择见解析;(1);(2)单调增区间为.
【详解】
解:(1)选择①:因为
所以,其中,
所以,又因为,所以.
选择②:,所以.
(2)因为
所以
则,
,
所以函数的单调增区间为
(一个都没写的扣一分)
同课章节目录
