2.2 位移变化规律 教案
文档属性
| 名称 | 2.2 位移变化规律 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 307.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-03 18:13:26 | ||
图片预览


文档简介
位移变化规律
【教材分析】
匀变速直线运动是运动学的重要组成部分,是学生学习运动学的基础。本节内容是在学习了速度公式的基础上对匀变速直线运动规律的进一步探究,又是以后学习运动学的基础,具有承上启下的作用。本节课是学生第一次用微积分的数学思维来推导物理规律,培养学生利用数学思维来研究物理问题的能力。
【教学目标】
1.物理观念:能用公式、图像等方法研究匀变速直线运动,能用匀变速直线运动的规律解释生活中的一些现象,具有与直线运动相关的初步的运动观念。
2.科学思维:能在特定情境中运用匀变速直线运动模型解决问题。
3.科学探究:用科学研究中的极限方法分析物理问题,通过推理,获得结论。
4.科学态度与责任:通过观察生活中的匀变速直线运动,使学生感受物理来源于生活的思想;通过师生合作探究,提高学生的合作、交流能力。
【教学重点】
位移公式的推导及应用,利用位移公式、位移——速度公式解决问题。
【教学难点】
利用微积分方法推导位移公式。
【教学过程】
一、导入新课
做匀速直线运动的汽车,速度—时间满足关系
问题:位移与时间到底存在什么样的关系呢?
二、匀变速直线运动位移—时间关系
1.位移在v-t图像中的表示:
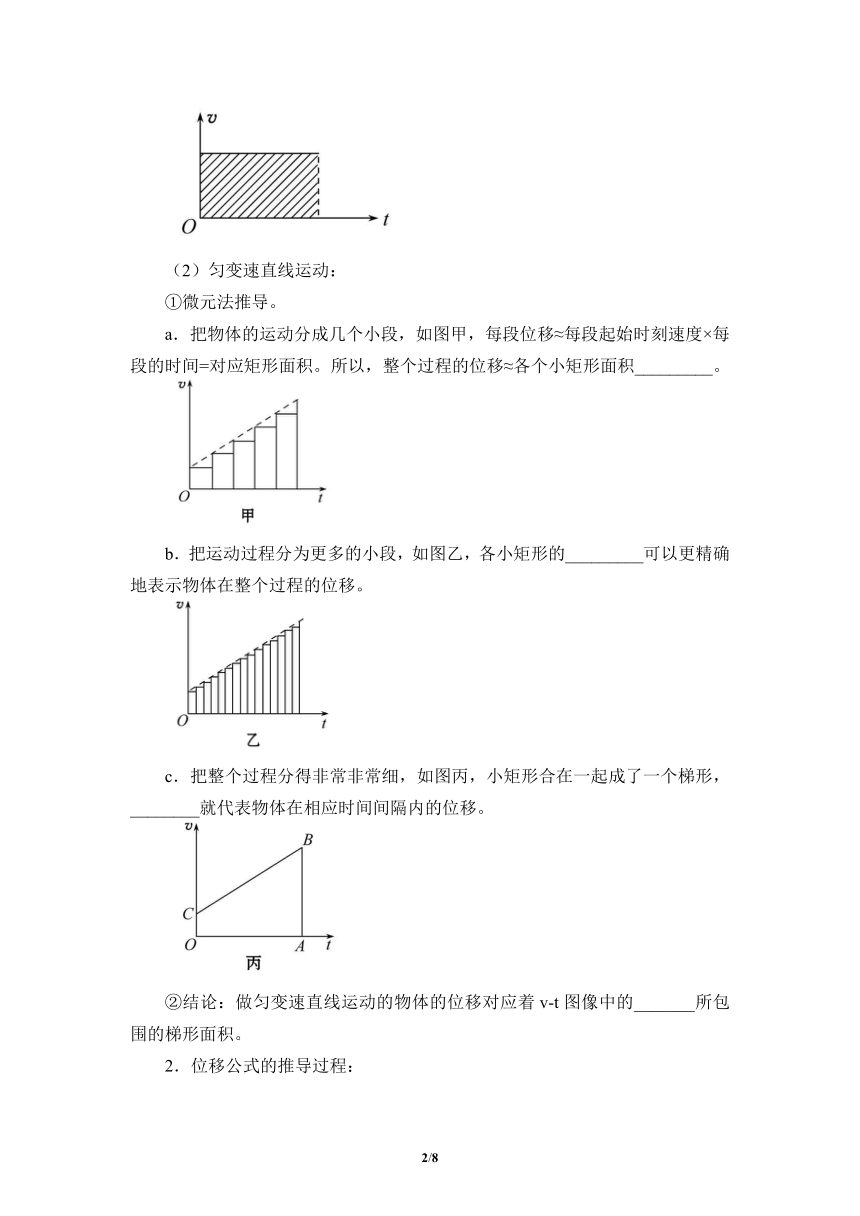
(1)匀速运动:如图所示,在匀速直线运动中,v-t图像与t轴所围矩形“面积”表示_________。
(2)匀变速直线运动:
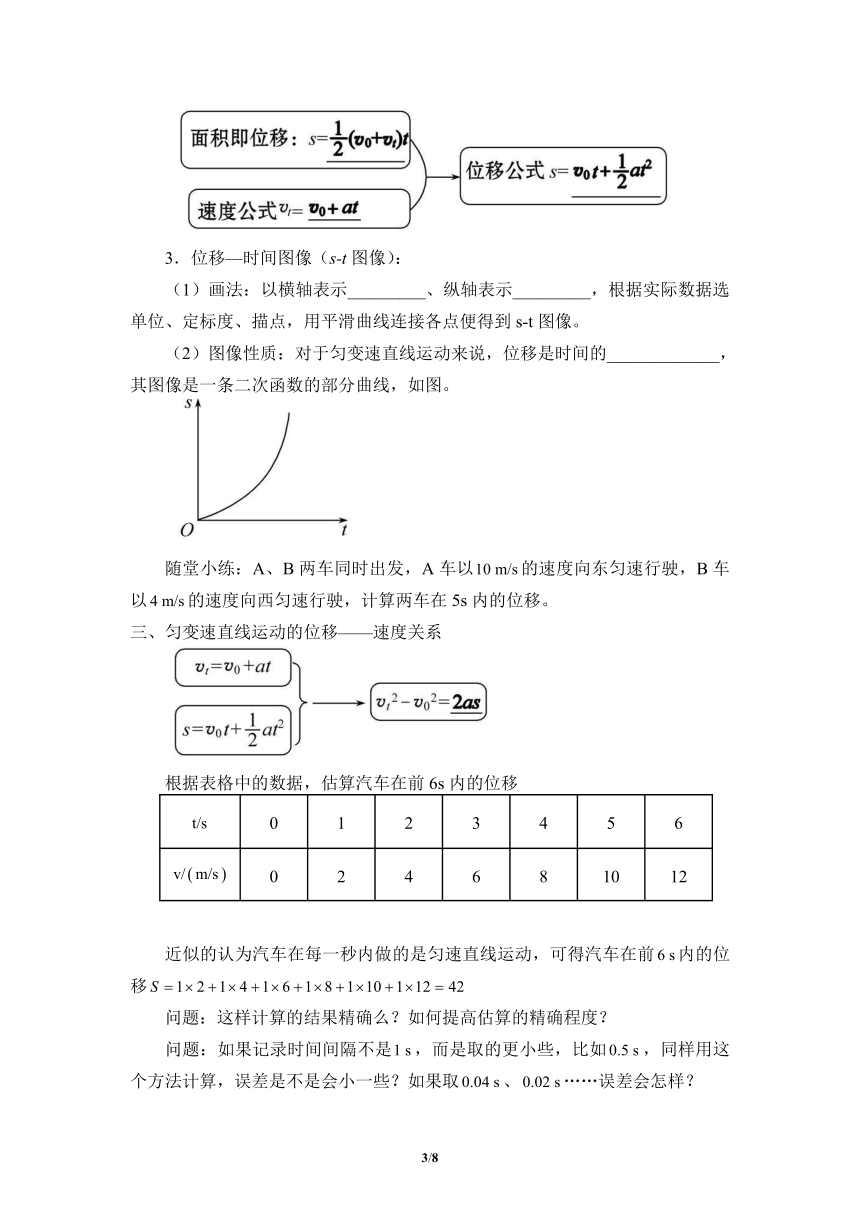
①微元法推导。
a.把物体的运动分成几个小段,如图甲,每段位移≈每段起始时刻速度×每段的时间=对应矩形面积。所以,整个过程的位移≈各个小矩形面积_________。
b.把运动过程分为更多的小段,如图乙,各小矩形的_________可以更精确地表示物体在整个过程的位移。
c.把整个过程分得非常非常细,如图丙,小矩形合在一起成了一个梯形,________就代表物体在相应时间间隔内的位移。
②结论:做匀变速直线运动的物体的位移对应着v-t图像中的_______所包围的梯形面积。
2.位移公式的推导过程:
3.位移—时间图像(s-t图像):
(1)画法:以横轴表示_________、纵轴表示_________,根据实际数据选单位、定标度、描点,用平滑曲线连接各点便得到s-t图像。
(2)图像性质:对于匀变速直线运动来说,位移是时间的_____________,其图像是一条二次函数的部分曲线,如图。
随堂小练:A、B两车同时出发,A车以的速度向东匀速行驶,B车以的速度向西匀速行驶,计算两车在5s内的位移。
三、匀变速直线运动的位移——速度关系
根据表格中的数据,估算汽车在前6s内的位移
0
1
2
3
4
5
6
0
2
4
6
8
10
12
近似的认为汽车在每一秒内做的是匀速直线运动,可得汽车在前内的位移
问题:这样计算的结果精确么?如何提高估算的精确程度?
问题:如果记录时间间隔不是,而是取的更小些,比如,同样用这个方法计算,误差是不是会小一些?如果取、……误差会怎样?
学生通过对这两个问题的思考,引导学生对极限思想在探究匀变速直线运动位移中的应用。通过极限方法,将复杂的匀变速直线运动转化为匀速直线运动来研究,将数学中的“微积分”思想植入到物理问题的研究中来。
例题:汽车从开始制动到停止所行驶的距离,是衡量汽车制动性能的参数之一。某型号的汽车以的速度在柏油路面上行驶,急刹车后做匀减速直线运动。若匀减速时的加速度大小是,开始制动后内汽车行驶的距离是多少?从开始制动到完全停止,汽车的行驶距离是多少?以此刹车问题为例,总结解题策略。
四、公式的应用
1.各物理量的意义:公式中表示时间内物体运动的位移,单位是;表示初速度,单位是;表示加速度,单位是;表示运动时间,单位是。
2.适用条件:公式反映了位移随时间的变化规律,公式仅适用于匀变速直线运动位移的求解。
3.符号规定:公式中、、都是矢量,应用时必须选取统一的正方向,一般选取初速度的方向为正方向。
(1)若与同向,取正值,物体做匀加速直线运动。
(2)若与反向,取负值,物体做匀减速直线运动。
(3)若位移的计算结果为正值,说明这段时间内位移的方向与规定的正方向相同。
(4)若位移的计算结果为负值,说明这段时间内位移的方向与规定的正方向相反。
4.若,则,位移与时间的二次方成正比。
5.思考·讨论:利用公式求出的位移大小等于物体运动的路程吗?
6.典例示范:(2019·福州高一检测)一辆卡车初速度为,以的加速度行驶,求:
(1)卡车在末的速度大小。
(2)卡车在内的位移大小。
(3)卡车在第内的位移大小。
7.误区警示:应用位移公式的两点注意
(1)公式仅适用于匀变速直线运动。
(2)应用位移公式解题时常选初速度的方向为正方向,
物体若加速则加速度为正值,减速则加速度为负值。
[素养训练]
1.(多选)(2019·厦门高一检测)物体从静止开始做匀加速直线运动,第内通过的位移是,则( )
A.前的位移是
B.末的速度是
C.内的平均速度是
D.第内的平均速度是
2.从静止开始做匀加速直线运动的汽车,经过,走过位移。求:
(1)汽车运动的加速度大小。
(2)汽车末的速度。
用v-t图像求位移
五、匀速直线运动的位移:
(1)做匀速直线运动的物体在时间t内的位移。
(2)做匀速直线运动的物体,其v-t图像是一条平行于时间轴的直线,其位移在数值上等于v-t图线与对应的时间轴所包围的矩形的面积。如图所示。
2.匀变速直线运动的位移:
(1)如图所示,图线与时间轴所围的梯形的面积就代表物体在时间内的位移,梯形的上底为,下底为,
对应的时间为,则有:。
(2)因为t时刻的速度v=v0+at,所以位移与时间的关系
为。
[典例示范]
(多选)(2019·龙岩高一检测)某物体运动的v-t图像如图所示,根据图像可知,该物体( )
A.在0到末的时间内,加速度为
B.在0到末的时间内,位移为
C.在0到末的时间内,位移为
D.在0到末的时间内,位移为
[误区警示]分析v-t图像的两大误区
(1)把v-t图像和s-t图像混淆不清。例如:把v-t图像中两条直线的交点误认为相遇,在s-t图像中根据直线向上倾斜、向下倾斜判断运动方向等等。
(2)把v-t图像误认为是质点的运动轨迹。v-t图像与坐标轴围成的图形的“面积”在横轴上方为“正”,在横轴下方为“负”;这“面积”的代数和表示对应时间内发生的位移,这“面积”的绝对值之和表示对应时间内的路程。
[素养训练]
1.(多选)甲、乙两个物体在同一地点,沿同一方向做直线运动的速度—时间图像如图所示,关于内甲、乙的运动说法正确的是( )
A.两物体相遇的时间是和
B.内甲在乙前面,内乙在甲前面
C.两个物体相距最远的时刻是末
D.时乙的加速度为
2.(多选)(2019·三明高一检测)甲、乙两个物体沿同一直线运动,它们的速度图像如图所示。由图像可知( )
A.甲运动时的加速度为
B.乙运动时的加速度为
C.从开始计时到甲、乙速度相同的过程中,甲的位移为,乙的位移为
D.甲、乙沿相反方向运动
六、位移、速度关系的应用
1.适用条件:公式表述的是匀变速直线运动的速度与位移的关系,适用于匀变速直线运动。
2.意义:公式反映了初速度、末速度、加速度、位移之间的关系,当其中三个物理量已知时,可求另一个未知量。
3.公式的矢量性:公式中、、、都是矢量,应用时必须选取统一的正方向,一般选方向为正方向。
(1)物体做加速运动时,取正值,做减速运动时,取负值。
(2),说明物体通过的位移方向与初速度方向相同;,说明位移的方向与初速度的方向相反。
4.两种特殊形式:
(1)当时,(初速度为零的匀加速直线运动)
(2)当时,(末速度为零的匀减速直线运动)
[思考·讨论]
情境:如图所示,狙击步枪射击时,若把子弹在枪筒中的运动看作是匀加速直线运动,假设枪筒长,子弹的加速度为。
讨论:(1)根据速度公式和位移公式求子弹射出枪口时的速度。
(2)在上面问题中,已知条件和所求的结果都不涉及时间,它只是一个中间量,能否将两个公式联立,消去,只用一个关系式表示位移与速度的关系呢?
[规律方法]公式的应用技巧
(1)当物体做匀变速直线运动时,如果不涉及时间一般用速度位移公式较方便。
(2)刹车问题由于末速度为零,应用此公式往往较方便。
8/8
【教材分析】
匀变速直线运动是运动学的重要组成部分,是学生学习运动学的基础。本节内容是在学习了速度公式的基础上对匀变速直线运动规律的进一步探究,又是以后学习运动学的基础,具有承上启下的作用。本节课是学生第一次用微积分的数学思维来推导物理规律,培养学生利用数学思维来研究物理问题的能力。
【教学目标】
1.物理观念:能用公式、图像等方法研究匀变速直线运动,能用匀变速直线运动的规律解释生活中的一些现象,具有与直线运动相关的初步的运动观念。
2.科学思维:能在特定情境中运用匀变速直线运动模型解决问题。
3.科学探究:用科学研究中的极限方法分析物理问题,通过推理,获得结论。
4.科学态度与责任:通过观察生活中的匀变速直线运动,使学生感受物理来源于生活的思想;通过师生合作探究,提高学生的合作、交流能力。
【教学重点】
位移公式的推导及应用,利用位移公式、位移——速度公式解决问题。
【教学难点】
利用微积分方法推导位移公式。
【教学过程】
一、导入新课
做匀速直线运动的汽车,速度—时间满足关系
问题:位移与时间到底存在什么样的关系呢?
二、匀变速直线运动位移—时间关系
1.位移在v-t图像中的表示:
(1)匀速运动:如图所示,在匀速直线运动中,v-t图像与t轴所围矩形“面积”表示_________。
(2)匀变速直线运动:
①微元法推导。
a.把物体的运动分成几个小段,如图甲,每段位移≈每段起始时刻速度×每段的时间=对应矩形面积。所以,整个过程的位移≈各个小矩形面积_________。
b.把运动过程分为更多的小段,如图乙,各小矩形的_________可以更精确地表示物体在整个过程的位移。
c.把整个过程分得非常非常细,如图丙,小矩形合在一起成了一个梯形,________就代表物体在相应时间间隔内的位移。
②结论:做匀变速直线运动的物体的位移对应着v-t图像中的_______所包围的梯形面积。
2.位移公式的推导过程:
3.位移—时间图像(s-t图像):
(1)画法:以横轴表示_________、纵轴表示_________,根据实际数据选单位、定标度、描点,用平滑曲线连接各点便得到s-t图像。
(2)图像性质:对于匀变速直线运动来说,位移是时间的_____________,其图像是一条二次函数的部分曲线,如图。
随堂小练:A、B两车同时出发,A车以的速度向东匀速行驶,B车以的速度向西匀速行驶,计算两车在5s内的位移。
三、匀变速直线运动的位移——速度关系
根据表格中的数据,估算汽车在前6s内的位移
0
1
2
3
4
5
6
0
2
4
6
8
10
12
近似的认为汽车在每一秒内做的是匀速直线运动,可得汽车在前内的位移
问题:这样计算的结果精确么?如何提高估算的精确程度?
问题:如果记录时间间隔不是,而是取的更小些,比如,同样用这个方法计算,误差是不是会小一些?如果取、……误差会怎样?
学生通过对这两个问题的思考,引导学生对极限思想在探究匀变速直线运动位移中的应用。通过极限方法,将复杂的匀变速直线运动转化为匀速直线运动来研究,将数学中的“微积分”思想植入到物理问题的研究中来。
例题:汽车从开始制动到停止所行驶的距离,是衡量汽车制动性能的参数之一。某型号的汽车以的速度在柏油路面上行驶,急刹车后做匀减速直线运动。若匀减速时的加速度大小是,开始制动后内汽车行驶的距离是多少?从开始制动到完全停止,汽车的行驶距离是多少?以此刹车问题为例,总结解题策略。
四、公式的应用
1.各物理量的意义:公式中表示时间内物体运动的位移,单位是;表示初速度,单位是;表示加速度,单位是;表示运动时间,单位是。
2.适用条件:公式反映了位移随时间的变化规律,公式仅适用于匀变速直线运动位移的求解。
3.符号规定:公式中、、都是矢量,应用时必须选取统一的正方向,一般选取初速度的方向为正方向。
(1)若与同向,取正值,物体做匀加速直线运动。
(2)若与反向,取负值,物体做匀减速直线运动。
(3)若位移的计算结果为正值,说明这段时间内位移的方向与规定的正方向相同。
(4)若位移的计算结果为负值,说明这段时间内位移的方向与规定的正方向相反。
4.若,则,位移与时间的二次方成正比。
5.思考·讨论:利用公式求出的位移大小等于物体运动的路程吗?
6.典例示范:(2019·福州高一检测)一辆卡车初速度为,以的加速度行驶,求:
(1)卡车在末的速度大小。
(2)卡车在内的位移大小。
(3)卡车在第内的位移大小。
7.误区警示:应用位移公式的两点注意
(1)公式仅适用于匀变速直线运动。
(2)应用位移公式解题时常选初速度的方向为正方向,
物体若加速则加速度为正值,减速则加速度为负值。
[素养训练]
1.(多选)(2019·厦门高一检测)物体从静止开始做匀加速直线运动,第内通过的位移是,则( )
A.前的位移是
B.末的速度是
C.内的平均速度是
D.第内的平均速度是
2.从静止开始做匀加速直线运动的汽车,经过,走过位移。求:
(1)汽车运动的加速度大小。
(2)汽车末的速度。
用v-t图像求位移
五、匀速直线运动的位移:
(1)做匀速直线运动的物体在时间t内的位移。
(2)做匀速直线运动的物体,其v-t图像是一条平行于时间轴的直线,其位移在数值上等于v-t图线与对应的时间轴所包围的矩形的面积。如图所示。
2.匀变速直线运动的位移:
(1)如图所示,图线与时间轴所围的梯形的面积就代表物体在时间内的位移,梯形的上底为,下底为,
对应的时间为,则有:。
(2)因为t时刻的速度v=v0+at,所以位移与时间的关系
为。
[典例示范]
(多选)(2019·龙岩高一检测)某物体运动的v-t图像如图所示,根据图像可知,该物体( )
A.在0到末的时间内,加速度为
B.在0到末的时间内,位移为
C.在0到末的时间内,位移为
D.在0到末的时间内,位移为
[误区警示]分析v-t图像的两大误区
(1)把v-t图像和s-t图像混淆不清。例如:把v-t图像中两条直线的交点误认为相遇,在s-t图像中根据直线向上倾斜、向下倾斜判断运动方向等等。
(2)把v-t图像误认为是质点的运动轨迹。v-t图像与坐标轴围成的图形的“面积”在横轴上方为“正”,在横轴下方为“负”;这“面积”的代数和表示对应时间内发生的位移,这“面积”的绝对值之和表示对应时间内的路程。
[素养训练]
1.(多选)甲、乙两个物体在同一地点,沿同一方向做直线运动的速度—时间图像如图所示,关于内甲、乙的运动说法正确的是( )
A.两物体相遇的时间是和
B.内甲在乙前面,内乙在甲前面
C.两个物体相距最远的时刻是末
D.时乙的加速度为
2.(多选)(2019·三明高一检测)甲、乙两个物体沿同一直线运动,它们的速度图像如图所示。由图像可知( )
A.甲运动时的加速度为
B.乙运动时的加速度为
C.从开始计时到甲、乙速度相同的过程中,甲的位移为,乙的位移为
D.甲、乙沿相反方向运动
六、位移、速度关系的应用
1.适用条件:公式表述的是匀变速直线运动的速度与位移的关系,适用于匀变速直线运动。
2.意义:公式反映了初速度、末速度、加速度、位移之间的关系,当其中三个物理量已知时,可求另一个未知量。
3.公式的矢量性:公式中、、、都是矢量,应用时必须选取统一的正方向,一般选方向为正方向。
(1)物体做加速运动时,取正值,做减速运动时,取负值。
(2),说明物体通过的位移方向与初速度方向相同;,说明位移的方向与初速度的方向相反。
4.两种特殊形式:
(1)当时,(初速度为零的匀加速直线运动)
(2)当时,(末速度为零的匀减速直线运动)
[思考·讨论]
情境:如图所示,狙击步枪射击时,若把子弹在枪筒中的运动看作是匀加速直线运动,假设枪筒长,子弹的加速度为。
讨论:(1)根据速度公式和位移公式求子弹射出枪口时的速度。
(2)在上面问题中,已知条件和所求的结果都不涉及时间,它只是一个中间量,能否将两个公式联立,消去,只用一个关系式表示位移与速度的关系呢?
[规律方法]公式的应用技巧
(1)当物体做匀变速直线运动时,如果不涉及时间一般用速度位移公式较方便。
(2)刹车问题由于末速度为零,应用此公式往往较方便。
8/8
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
