12.2 三角形全等的判定 复习课件(共44张PPT)
文档属性
| 名称 | 12.2 三角形全等的判定 复习课件(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 00:00:00 | ||
图片预览

文档简介
(共44张PPT)
人教版
八年级上
复习全等三角形的判定
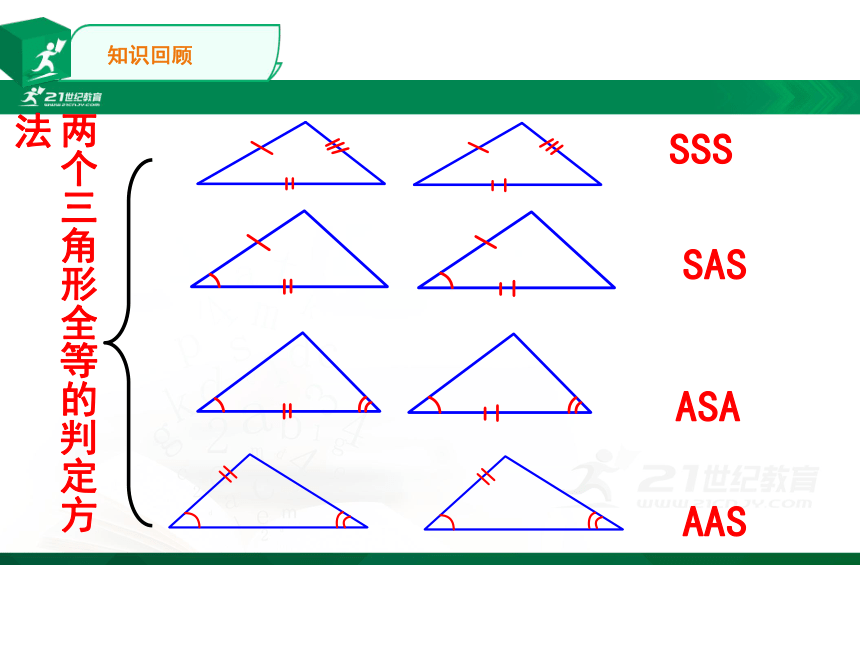
SSS
SAS
ASA
AAS
两个三角形全等的判定方法
知识回顾
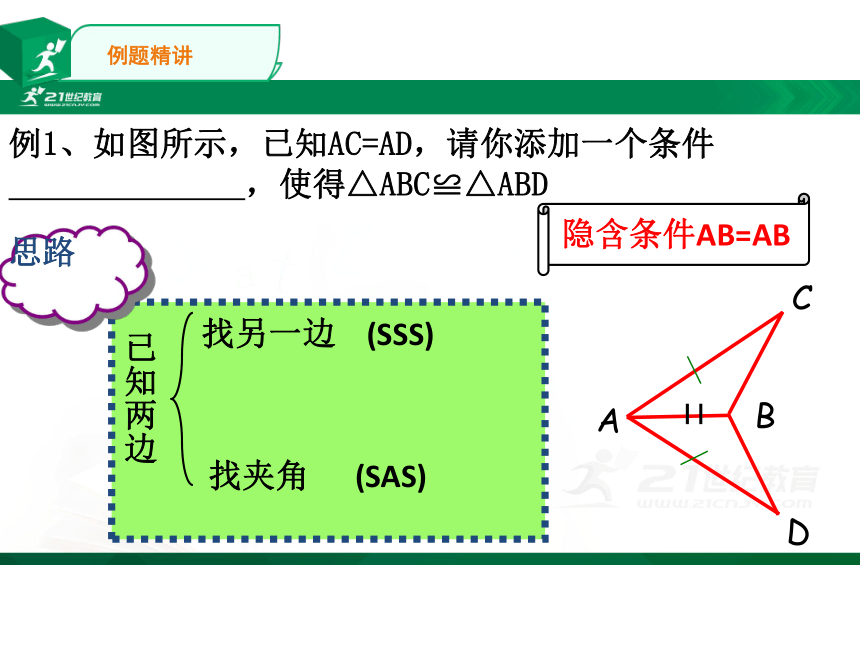
例1、如图所示,已知AC=AD,请你添加一个条件
,使得△ABC≌△ABD
B
A
C
D
思路
已知两边
找另一边
(SSS)
找夹角
(SAS)
隐含条件AB=AB
例题精讲
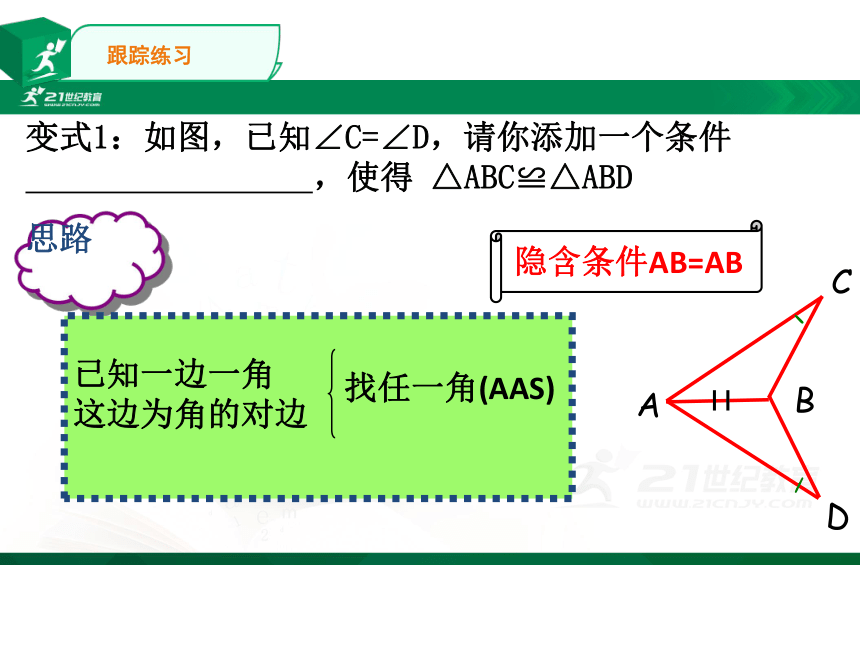
变式1:如图,已知∠C=∠D,请你添加一个条件
,使得
△ABC≌△ABD
B
A
C
D
思路
已知一边一角
这边为角的对边
找任一角(AAS)
隐含条件AB=AB
跟踪练习
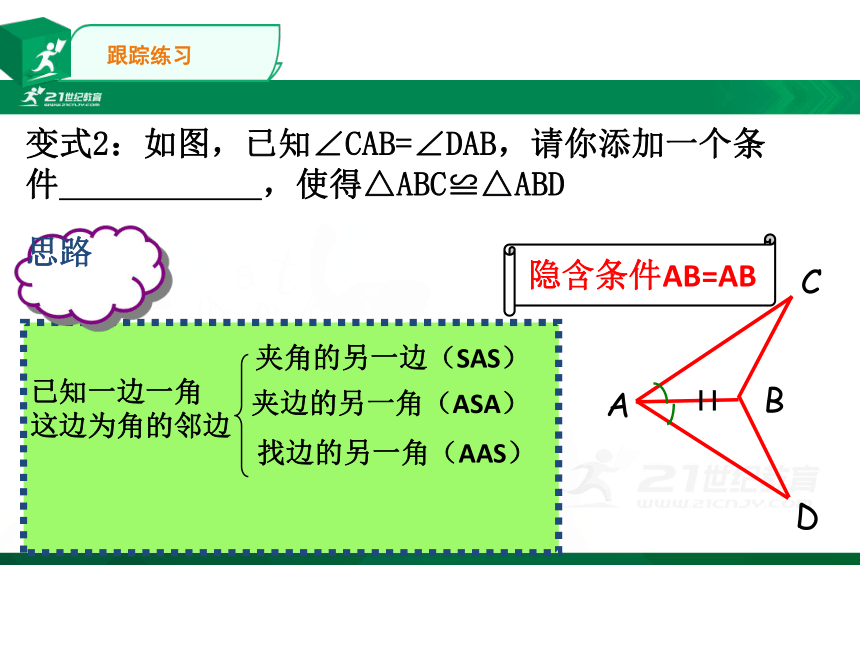
变式2:如图,已知∠CAB=∠DAB,请你添加一个条件
,使得△ABC≌△ABD
B
A
C
D
思路
已知一边一角
这边为角的邻边
夹角的另一边(SAS)
夹边的另一角(ASA)
找边的另一角(AAS)
隐含条件AB=AB
跟踪练习
A
D
E
C
B
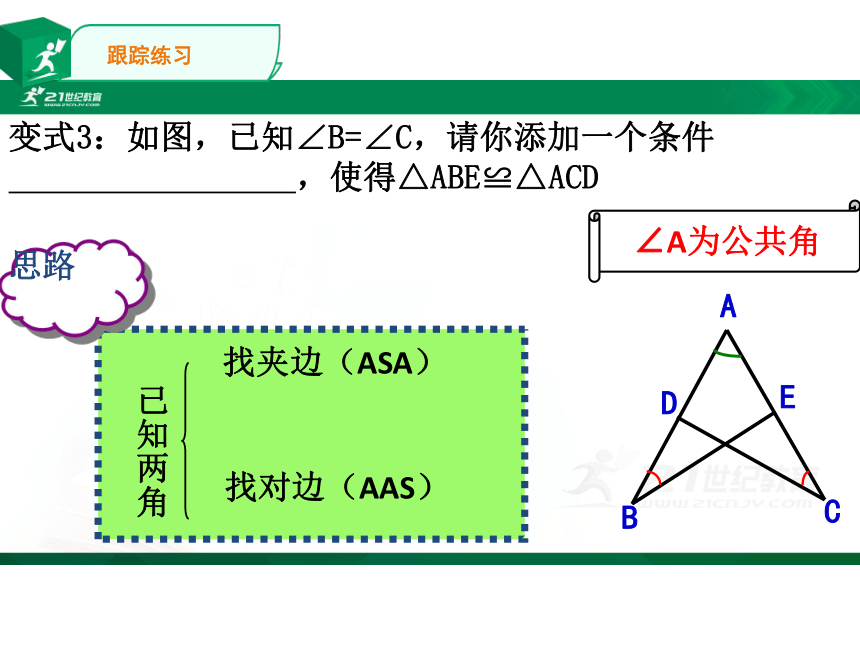
变式3:如图,已知∠B=∠C,请你添加一个条件
,使得△ABE≌△ACD
思路
已知两角
找夹边(ASA)
找对边(AAS)
∠A为公共角
跟踪练习
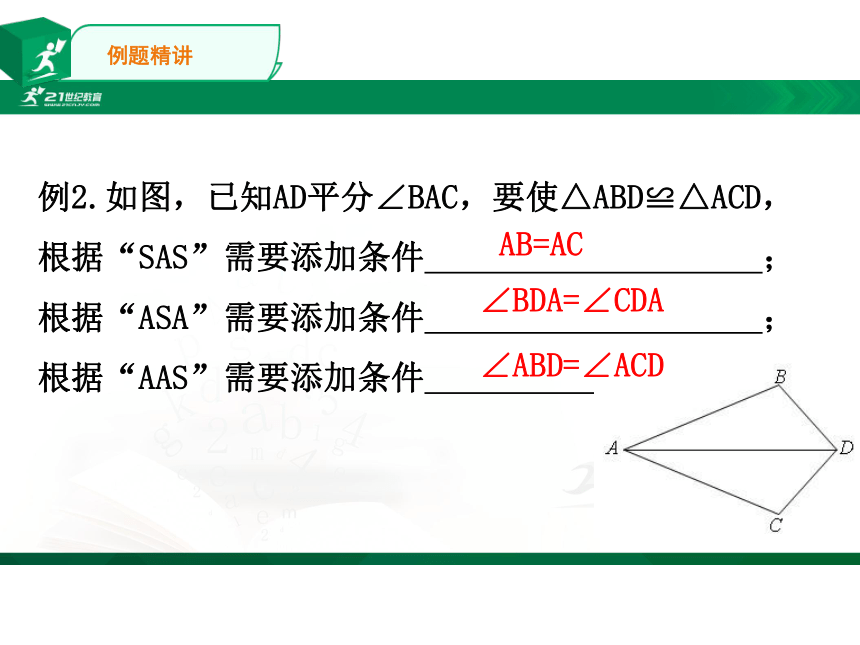
例2.如图,已知AD平分∠BAC,要使△ABD≌△ACD,
根据“SAS”需要添加条件
;
根据“ASA”需要添加条件
;
根据“AAS”需要添加条件
.
AB=AC
∠ABD=∠ACD
∠BDA=∠CDA
例题精讲
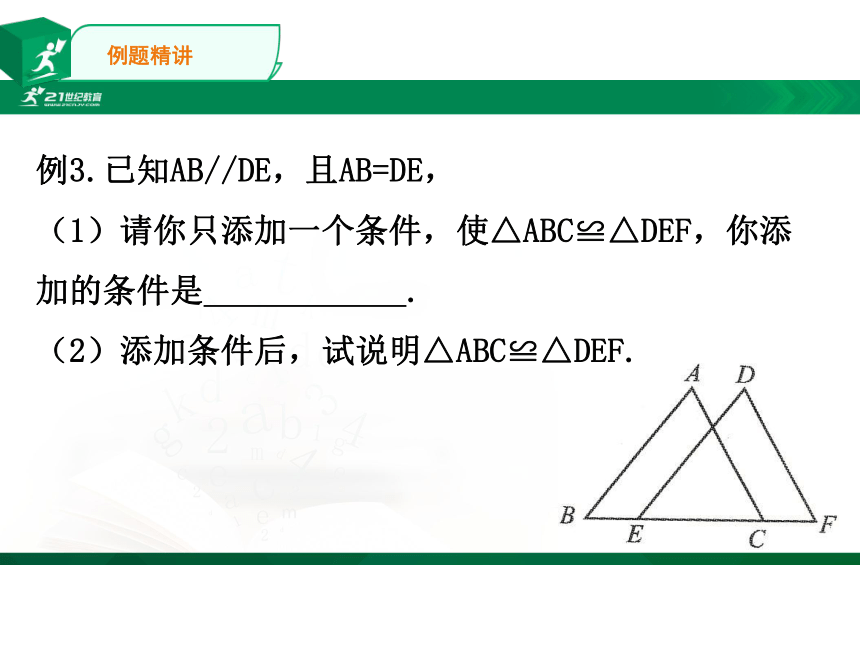
例3.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是
.
(2)添加条件后,试说明△ABC≌△DEF.
例题精讲
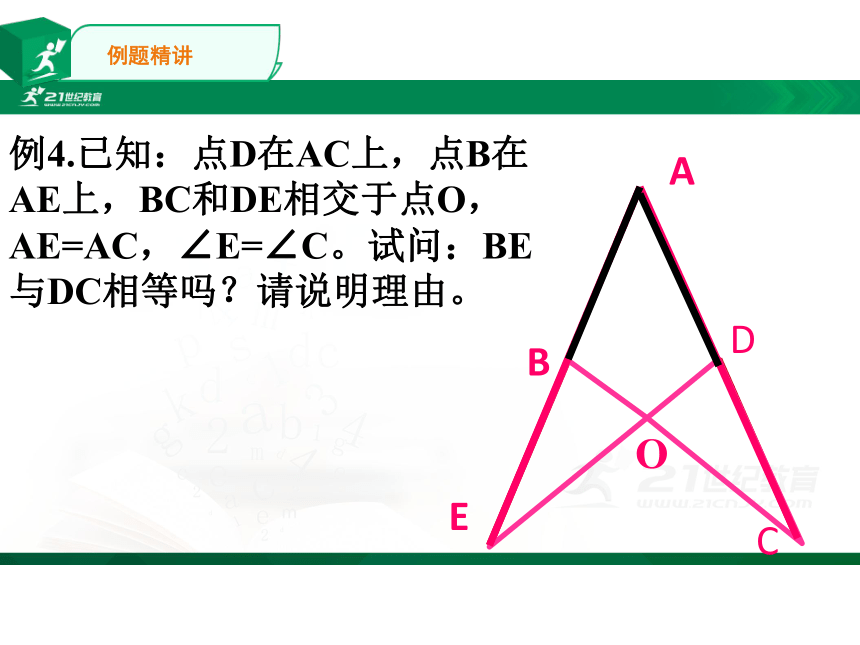
例4.已知:点D在AC上,点B在AE上,BC和DE相交于点O,AE=AC,∠E=∠C。试问:BE与DC相等吗?请说明理由。
B
D
C
O
E
A
例题精讲
B
E
D
C
A
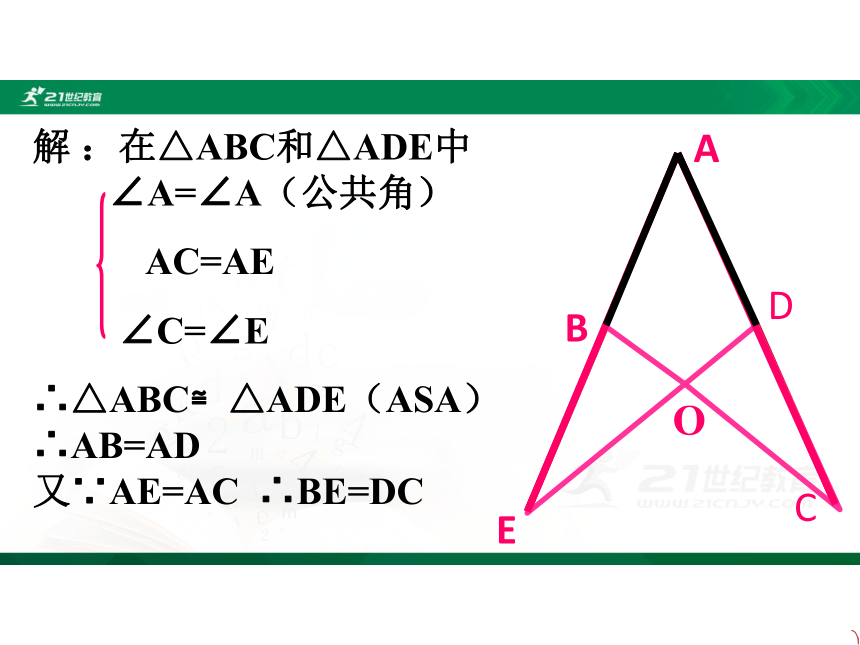
解
:在△ABC和△ADE中
∠A=∠A(公共角)
AC=AE
∠C=∠E
∴△ABC≌△ADE(ASA)∴AB=AD
又∵AE=AC
∴BE=DC
O
A
B
C
D
E
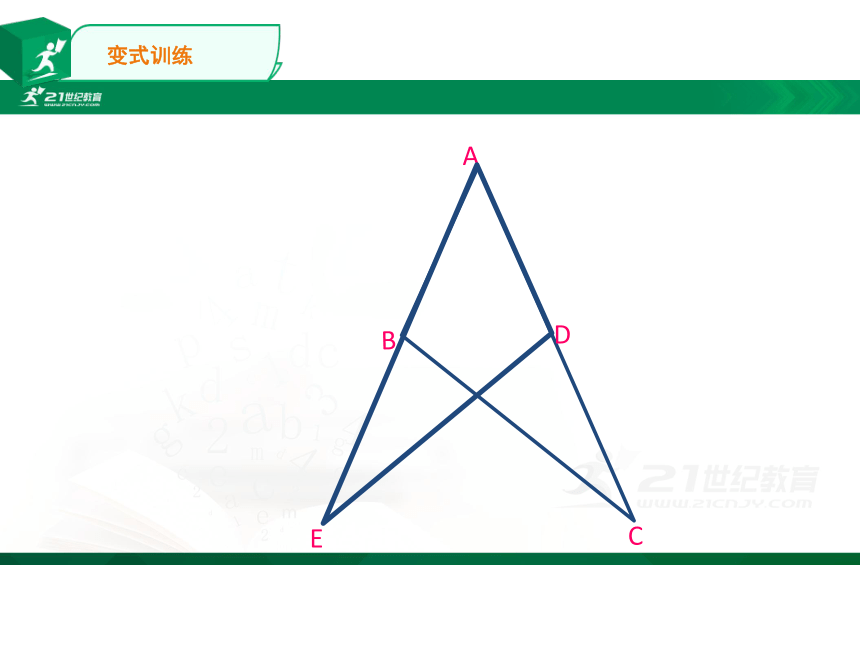
变式训练
变式训练
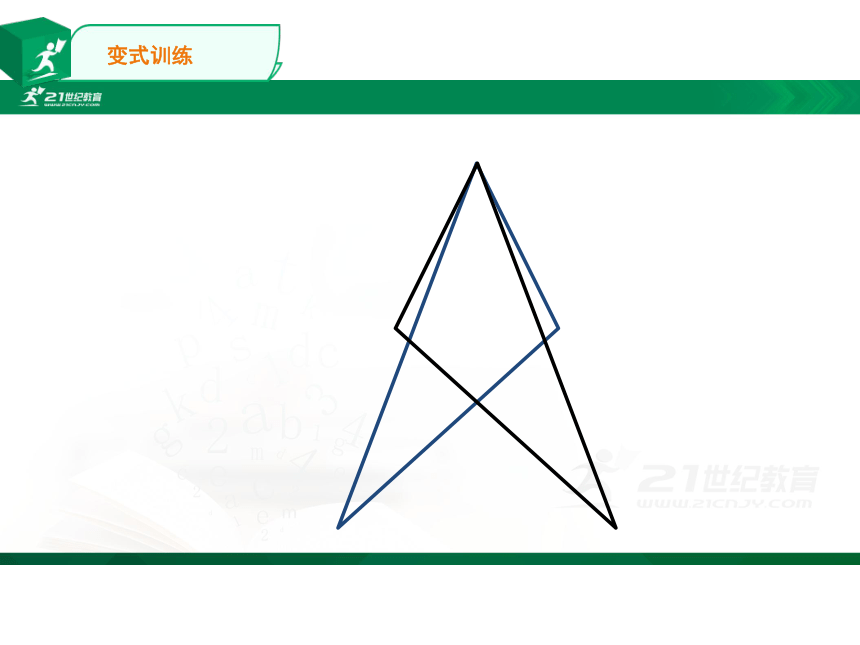
变式训练
A
B
C
D
E
变式训练
5.已知:
∠1=
∠2,
∠E=
∠C,AC=AE
试说明AB=AD
,∠B=
∠D的理由。
变式训练
A
B
C
D
E
1
2
解:
∵
∠1=
∠2
∴
∠1+
∠EAC=
∠2+
∠EAC
即
∠BAC=
∠DAE
在△BAC和
△DAE中
∠BAC=
∠DAE
AC=AE
∠C=
∠E
∴△
BAC
≌△
DAE
(ASA)
∴AB=AD
∠B=∠D
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
B
A
C
D
E
变式训练
5
.已知:
∠1=
∠2,∠E=
∠C,AC=AE,D、A、B在一条直线上;试说明点A的位置,并说明理由。
A
B
D
C
E
3
2
1
变式训练
B
A
D
C
E
1
2
3
解:∵
∠1=
∠2
∴
∠1+
∠3=
∠2+
∠3
∴
∠
DAE
=
∠
BAC
在△DAE和△BAC中
∠
DAE
=
∠
BAC
AE=AC
∠E=
∠C
∴
△DAE≌△BAC(ASA)
∴AD=AB
∴点A为线段DB中点
变式训练
A
B
C
D
E
6.如图所示,已知AB=AC,BD=CD,点E在AD的延长线上,说明BE=CE的理由
大大显身手
7.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且∠B+∠D=180°.
求证:AE=AD+BE.
F
大大显身手
8.等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线l的垂线,垂足分别为M、N.
(1)你能找到一对全等的三角形吗?并说明.
(2)BM,CN,MN之间有何关系?
(3)若将直线l旋转到如下图的位置,其他条件不变,那么上题的结论是否仍然成立?
大大显身手
小试牛刀:
如图:点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF,说明DE=BF的理由。
A
F
B
C
D
E
例3,如图,已知在AB,AC上各取一点D,E,使AD=AE,
连结BE,CD相交于O点,
∠1=∠2,试说明:
△ABO
≌△ACO
O
A
B
C
E
D
2
1
3
4
例5.如图,有一湖的湖岸在A,B之间呈一段圆弧状,A,B间的距离不能直接测得,你能用已学过的知识或方法设计测量方案,求出A,B间的距离吗?
A
B
.
C
D
E
例题精讲
A
D
B
O
C
例题精讲
1、结合题中条件和结论,选择恰当方法。
2、全等是说明线段或角相等的重要方法之一。
说明时注意:
①观察结论中的线段或角,在哪两个可能全等的三角形中。
②分析已有条件,欠缺条件,选择判定方法。
③公共边,公共角以及对顶角一般都是题中隐含的条件。
方法归纳
A
B
C
D
E
A1
B1
C1
C
D
E
如图1,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
(1)请说明△ABC
≌△CDE,并判断AC是否垂直CE?
(2)若将△ABC
沿BC方向平移至如图2的位置时,且其余条件不变,
则A1C1是否垂直CE?请说明为什么?
图1
图2
拓展提高
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。
A
C
B
D
?
你觉得他测得的距离准确吗?说明其中的理由。
解决问题
BC=
DC(
)
A
C
B
D
?
理由:在△ACB与△ACD中,
∠BAC=∠DAC
AC=AC(公共边)
∠ACB=∠ACD=90°
△ACB≌△ACD(ASA)
全等三角形的对应边相等
步测距离
碉堡距离
解决问题
https://www.21cnjy.com/help/help_extract.php
人教版
八年级上
复习全等三角形的判定
SSS
SAS
ASA
AAS
两个三角形全等的判定方法
知识回顾
例1、如图所示,已知AC=AD,请你添加一个条件
,使得△ABC≌△ABD
B
A
C
D
思路
已知两边
找另一边
(SSS)
找夹角
(SAS)
隐含条件AB=AB
例题精讲
变式1:如图,已知∠C=∠D,请你添加一个条件
,使得
△ABC≌△ABD
B
A
C
D
思路
已知一边一角
这边为角的对边
找任一角(AAS)
隐含条件AB=AB
跟踪练习
变式2:如图,已知∠CAB=∠DAB,请你添加一个条件
,使得△ABC≌△ABD
B
A
C
D
思路
已知一边一角
这边为角的邻边
夹角的另一边(SAS)
夹边的另一角(ASA)
找边的另一角(AAS)
隐含条件AB=AB
跟踪练习
A
D
E
C
B
变式3:如图,已知∠B=∠C,请你添加一个条件
,使得△ABE≌△ACD
思路
已知两角
找夹边(ASA)
找对边(AAS)
∠A为公共角
跟踪练习
例2.如图,已知AD平分∠BAC,要使△ABD≌△ACD,
根据“SAS”需要添加条件
;
根据“ASA”需要添加条件
;
根据“AAS”需要添加条件
.
AB=AC
∠ABD=∠ACD
∠BDA=∠CDA
例题精讲
例3.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是
.
(2)添加条件后,试说明△ABC≌△DEF.
例题精讲
例4.已知:点D在AC上,点B在AE上,BC和DE相交于点O,AE=AC,∠E=∠C。试问:BE与DC相等吗?请说明理由。
B
D
C
O
E
A
例题精讲
B
E
D
C
A
解
:在△ABC和△ADE中
∠A=∠A(公共角)
AC=AE
∠C=∠E
∴△ABC≌△ADE(ASA)∴AB=AD
又∵AE=AC
∴BE=DC
O
A
B
C
D
E
变式训练
变式训练
变式训练
A
B
C
D
E
变式训练
5.已知:
∠1=
∠2,
∠E=
∠C,AC=AE
试说明AB=AD
,∠B=
∠D的理由。
变式训练
A
B
C
D
E
1
2
解:
∵
∠1=
∠2
∴
∠1+
∠EAC=
∠2+
∠EAC
即
∠BAC=
∠DAE
在△BAC和
△DAE中
∠BAC=
∠DAE
AC=AE
∠C=
∠E
∴△
BAC
≌△
DAE
(ASA)
∴AB=AD
∠B=∠D
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
变式训练
B
A
C
D
E
变式训练
5
.已知:
∠1=
∠2,∠E=
∠C,AC=AE,D、A、B在一条直线上;试说明点A的位置,并说明理由。
A
B
D
C
E
3
2
1
变式训练
B
A
D
C
E
1
2
3
解:∵
∠1=
∠2
∴
∠1+
∠3=
∠2+
∠3
∴
∠
DAE
=
∠
BAC
在△DAE和△BAC中
∠
DAE
=
∠
BAC
AE=AC
∠E=
∠C
∴
△DAE≌△BAC(ASA)
∴AD=AB
∴点A为线段DB中点
变式训练
A
B
C
D
E
6.如图所示,已知AB=AC,BD=CD,点E在AD的延长线上,说明BE=CE的理由
大大显身手
7.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且∠B+∠D=180°.
求证:AE=AD+BE.
F
大大显身手
8.等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线l的垂线,垂足分别为M、N.
(1)你能找到一对全等的三角形吗?并说明.
(2)BM,CN,MN之间有何关系?
(3)若将直线l旋转到如下图的位置,其他条件不变,那么上题的结论是否仍然成立?
大大显身手
小试牛刀:
如图:点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF,说明DE=BF的理由。
A
F
B
C
D
E
例3,如图,已知在AB,AC上各取一点D,E,使AD=AE,
连结BE,CD相交于O点,
∠1=∠2,试说明:
△ABO
≌△ACO
O
A
B
C
E
D
2
1
3
4
例5.如图,有一湖的湖岸在A,B之间呈一段圆弧状,A,B间的距离不能直接测得,你能用已学过的知识或方法设计测量方案,求出A,B间的距离吗?
A
B
.
C
D
E
例题精讲
A
D
B
O
C
例题精讲
1、结合题中条件和结论,选择恰当方法。
2、全等是说明线段或角相等的重要方法之一。
说明时注意:
①观察结论中的线段或角,在哪两个可能全等的三角形中。
②分析已有条件,欠缺条件,选择判定方法。
③公共边,公共角以及对顶角一般都是题中隐含的条件。
方法归纳
A
B
C
D
E
A1
B1
C1
C
D
E
如图1,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
(1)请说明△ABC
≌△CDE,并判断AC是否垂直CE?
(2)若将△ABC
沿BC方向平移至如图2的位置时,且其余条件不变,
则A1C1是否垂直CE?请说明为什么?
图1
图2
拓展提高
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。
A
C
B
D
?
你觉得他测得的距离准确吗?说明其中的理由。
解决问题
BC=
DC(
)
A
C
B
D
?
理由:在△ACB与△ACD中,
∠BAC=∠DAC
AC=AC(公共边)
∠ACB=∠ACD=90°
△ACB≌△ACD(ASA)
全等三角形的对应边相等
步测距离
碉堡距离
解决问题
https://www.21cnjy.com/help/help_extract.php
