2021-2022学年北师大版九年级数学上册4.2平行线分线段成比例同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.2平行线分线段成比例同步练习题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 00:00:00 | ||
图片预览


文档简介
4.2平行线分线段成比例同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
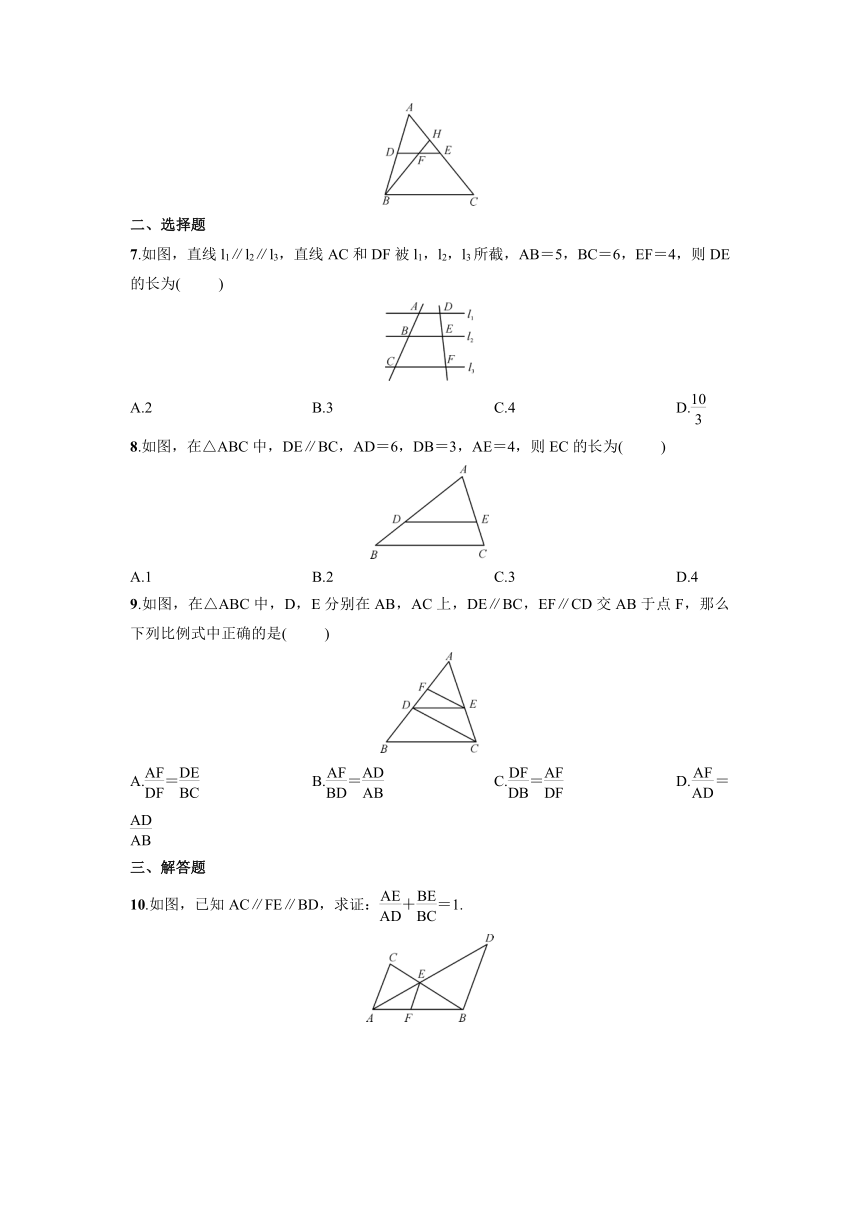
1.
如图,AB∥CD∥EF.若=,BD=5,则DF=_______.
2.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,则的值为_______.
3.
如图,已知l1∥l2∥l3,则=_______=_______.
4.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4
cm,则线段BC=_______cm.
5.如图,已知EG∥BC,GF∥CD,AE=3,EB=2,AF=6,则AD=_______.
6.如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则HE∶AH等于_______.
二、选择题
7.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为(
)
A.2
B.3
C.4
D.
8.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为(
)
A.1
B.2
C.3
D.4
9.如图,在△ABC中,D,E分别在AB,AC上,DE∥BC,EF∥CD交AB于点F,那么下列比例式中正确的是(
)
A.=
B.=
C.=
D.=
三、解答题
10.如图,已知AC∥FE∥BD,求证:+=1.
B组(中档题)
四、填空题
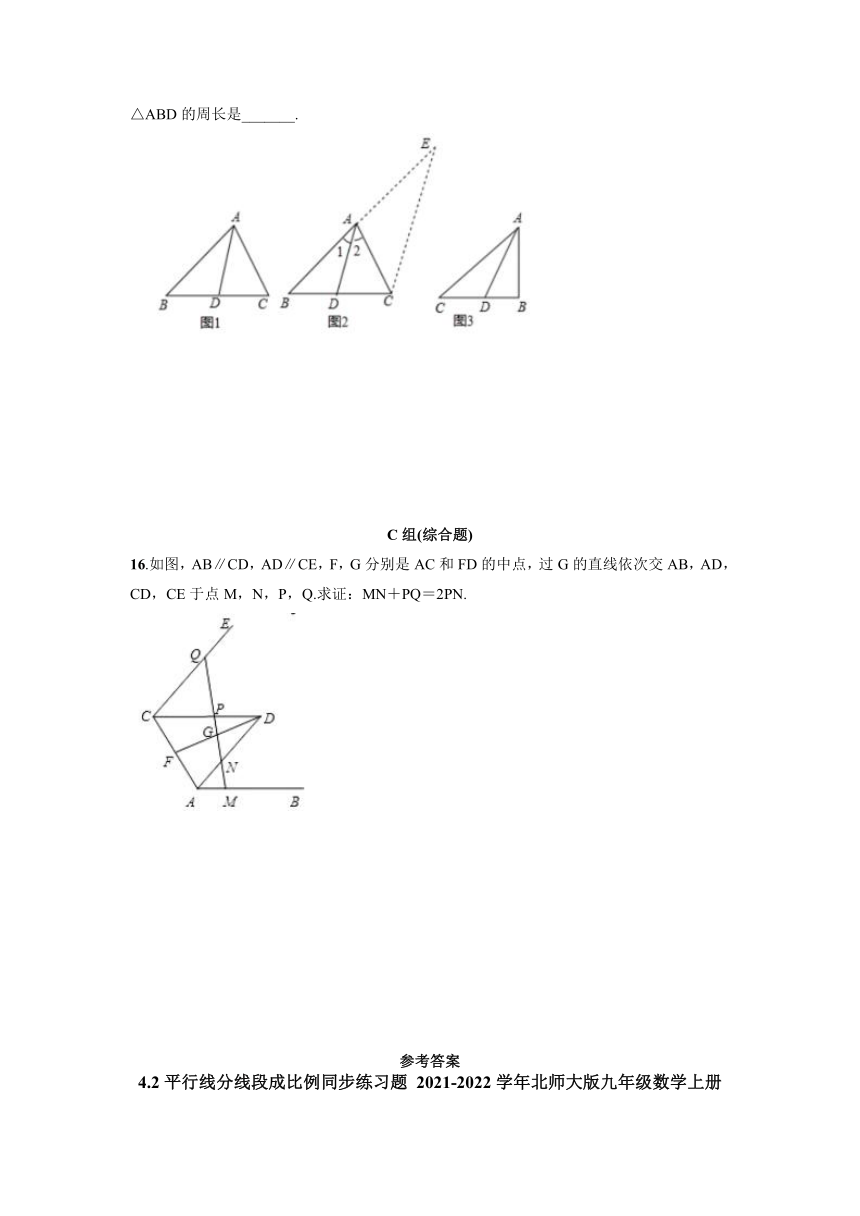
11.如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G,则CG=_______.
12.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE=_______。
13.如图,AD是△ABC的中线.
(1)若E为AD的中点,射线CE交AB于点F,则的值为_______.
(2)若E为AD上的一点,且=,射线CE交AB于点F,则的值为_______.
14.
如图,在△ABC中,D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于点E,则BE∶EC=_______.
五、解答题
15.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分.
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是_______.
C组(综合题)
16.如图,AB∥CD,AD∥CE,F,G分别是AC和FD的中点,过G的直线依次交AB,AD,CD,CE于点M,N,P,Q.求证:MN+PQ=2PN.
参考答案
4.2平行线分线段成比例同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.
如图,AB∥CD∥EF.若=,BD=5,则DF=10.
2.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,则的值为.
3.
如图,已知l1∥l2∥l3,则==.
4.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4
cm,则线段BC=12cm.
5.如图,已知EG∥BC,GF∥CD,AE=3,EB=2,AF=6,则AD=10.
6.如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则HE∶AH等于1∶2.
二、选择题
7.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为(
D
)
A.2
B.3
C.4
D.
8.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为(
B
)
A.1
B.2
C.3
D.4
9.如图,在△ABC中,D,E分别在AB,AC上,DE∥BC,EF∥CD交AB于点F,那么下列比例式中正确的是(
D
)
A.=
B.=
C.=
D.=
三、解答题
10.如图,已知AC∥FE∥BD,求证:+=1.
证明:∵AC∥EF,∴=①.
∵FE∥BD,∴=②.
①+②,得+=+==1,
即+=1.
B组(中档题)
四、填空题
11.如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G,则CG=-1.
12.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE=.
13.如图,AD是△ABC的中线.
(1)若E为AD的中点,射线CE交AB于点F,则的值为.
(2)若E为AD上的一点,且=,射线CE交AB于点F,则的值为.
14.
如图,在△ABC中,D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于点E,则BE∶EC=1∶3.
五、解答题
15.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分.
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是.
证明:过点C作CE∥DA,交BA的延长线于点E,
∴=,∠2=∠ACE,∠1=∠E.
∵AD平分∠BAC,∴∠1=∠2.
∴∠ACE=∠E.∴AE=AC.
∴=.
C组(综合题)
16.如图,AB∥CD,AD∥CE,F,G分别是AC和FD的中点,过G的直线依次交AB,AD,CD,CE于点M,N,P,Q.求证:MN+PQ=2PN.
证明:延长BA,EC,设交点为O,则四边形OADC为平行四边形,连接OF.
∵F是AC的中点,
∴F是?OADC的对称中心.
∴O,F,D三点共线,且F是OD的中点.
∵G是FD的中点,∴=.
∵AB∥CD,∴=.
∵AD∥CE,∴=.
∴+=+=.
∵==,∴OQ=3DN.
∴CQ=OQ-OC=3DN-OC=3DN-AD,AN=AD-DN.
∴AN+CQ=2DN.∴+==2.
∴MN+PQ=2PN.
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.
如图,AB∥CD∥EF.若=,BD=5,则DF=_______.
2.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,则的值为_______.
3.
如图,已知l1∥l2∥l3,则=_______=_______.
4.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4
cm,则线段BC=_______cm.
5.如图,已知EG∥BC,GF∥CD,AE=3,EB=2,AF=6,则AD=_______.
6.如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则HE∶AH等于_______.
二、选择题
7.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为(
)
A.2
B.3
C.4
D.
8.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为(
)
A.1
B.2
C.3
D.4
9.如图,在△ABC中,D,E分别在AB,AC上,DE∥BC,EF∥CD交AB于点F,那么下列比例式中正确的是(
)
A.=
B.=
C.=
D.=
三、解答题
10.如图,已知AC∥FE∥BD,求证:+=1.
B组(中档题)
四、填空题
11.如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G,则CG=_______.
12.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE=_______。
13.如图,AD是△ABC的中线.
(1)若E为AD的中点,射线CE交AB于点F,则的值为_______.
(2)若E为AD上的一点,且=,射线CE交AB于点F,则的值为_______.
14.
如图,在△ABC中,D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于点E,则BE∶EC=_______.
五、解答题
15.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分.
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是_______.
C组(综合题)
16.如图,AB∥CD,AD∥CE,F,G分别是AC和FD的中点,过G的直线依次交AB,AD,CD,CE于点M,N,P,Q.求证:MN+PQ=2PN.
参考答案
4.2平行线分线段成比例同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.
如图,AB∥CD∥EF.若=,BD=5,则DF=10.
2.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,则的值为.
3.
如图,已知l1∥l2∥l3,则==.
4.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4
cm,则线段BC=12cm.
5.如图,已知EG∥BC,GF∥CD,AE=3,EB=2,AF=6,则AD=10.
6.如图,DE是△ABC的中位线,F是DE的中点,BF的延长线交AC于点H,则HE∶AH等于1∶2.
二、选择题
7.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为(
D
)
A.2
B.3
C.4
D.
8.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为(
B
)
A.1
B.2
C.3
D.4
9.如图,在△ABC中,D,E分别在AB,AC上,DE∥BC,EF∥CD交AB于点F,那么下列比例式中正确的是(
D
)
A.=
B.=
C.=
D.=
三、解答题
10.如图,已知AC∥FE∥BD,求证:+=1.
证明:∵AC∥EF,∴=①.
∵FE∥BD,∴=②.
①+②,得+=+==1,
即+=1.
B组(中档题)
四、填空题
11.如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G,则CG=-1.
12.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE=.
13.如图,AD是△ABC的中线.
(1)若E为AD的中点,射线CE交AB于点F,则的值为.
(2)若E为AD上的一点,且=,射线CE交AB于点F,则的值为.
14.
如图,在△ABC中,D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于点E,则BE∶EC=1∶3.
五、解答题
15.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分.
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是.
证明:过点C作CE∥DA,交BA的延长线于点E,
∴=,∠2=∠ACE,∠1=∠E.
∵AD平分∠BAC,∴∠1=∠2.
∴∠ACE=∠E.∴AE=AC.
∴=.
C组(综合题)
16.如图,AB∥CD,AD∥CE,F,G分别是AC和FD的中点,过G的直线依次交AB,AD,CD,CE于点M,N,P,Q.求证:MN+PQ=2PN.
证明:延长BA,EC,设交点为O,则四边形OADC为平行四边形,连接OF.
∵F是AC的中点,
∴F是?OADC的对称中心.
∴O,F,D三点共线,且F是OD的中点.
∵G是FD的中点,∴=.
∵AB∥CD,∴=.
∵AD∥CE,∴=.
∴+=+=.
∵==,∴OQ=3DN.
∴CQ=OQ-OC=3DN-OC=3DN-AD,AN=AD-DN.
∴AN+CQ=2DN.∴+==2.
∴MN+PQ=2PN.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
