2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.4探索三角形相似的条件同步练习题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 121.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 00:00:00 | ||
图片预览




文档简介
4.4探索三角形相似的条件同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
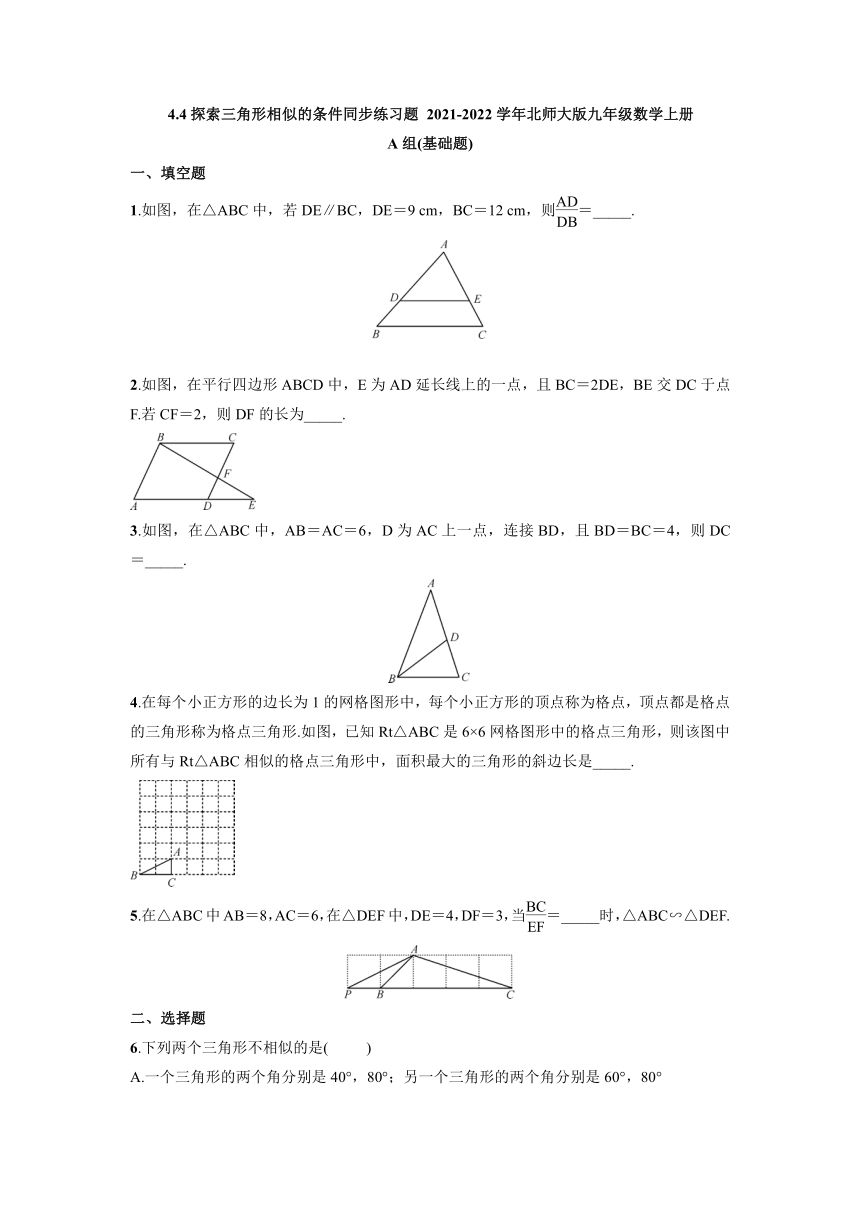
1.如图,在△ABC中,若DE∥BC,DE=9
cm,BC=12
cm,则=_____.
2.如图,在平行四边形ABCD中,E为AD延长线上的一点,且BC=2DE,BE交DC于点F.若CF=2,则DF的长为_____.
3.如图,在△ABC中,AB=AC=6,D为AC上一点,连接BD,且BD=BC=4,则DC=_____.
4.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是_____.
5.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=_____时,△ABC∽△DEF.
二、选择题
6.下列两个三角形不相似的是(
)
A.一个三角形的两个角分别是40°,80°;另一个三角形的两个角分别是60°,80°
B.一个三角形的三边长分别是4
cm,6
cm,8
cm;另一个三角形的三边长分别是12
cm,18
cm,21
cm
C.一个三角形的两边长分别是2
cm和5
cm,夹角是40°;另一个三角形的两边长分别是3
cm和7.5
cm,夹角是40°
D.各有一个角是120°的两个等腰三角形
7.如图,已知∠DAB=∠CAE,那么添加下列一个条件后,仍然无法判定△ABC∽△ADE的是(
)
A.=
B.=
C.∠B=∠D
D.∠C=∠AED
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为(
)
A.
B.
C.
D.
9.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
)
A.F
B.G
C.H
D.K
三、解答题
10.如图,四边形ABCD的对角形AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
11.如图,已知==,求证:△ABD∽△ACE.
B组(中档题)
四、填空题
12.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则EF=_____.
13.如图,△ABC中,AD1=AB,D1D2=D1B,D2D3=D2B,…,照这样继续下去,D2
020D2
021=D2
020B,且D1E1∥BC,D2E2∥BC,D2E3∥BC;…,D2
021E2
021∥BC,则=_____.
五、解答题
14.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM交DB于点N.
(1)求证:BD2=AD·CD.
(2)若CD=6,AD=8,则MN=.
C组(综合题)
15.如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是_____.
(2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
参考答案
4.4探索三角形相似的条件同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
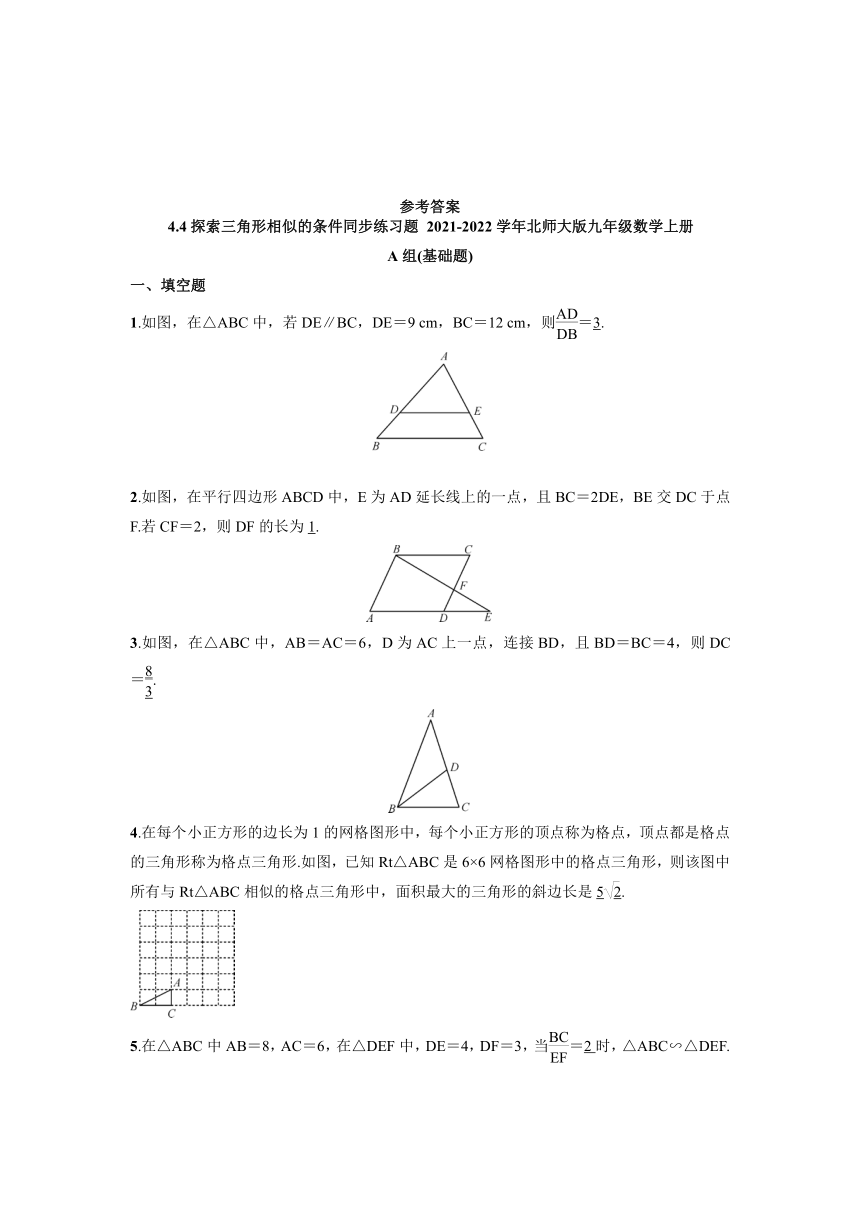
1.如图,在△ABC中,若DE∥BC,DE=9
cm,BC=12
cm,则=3.
2.如图,在平行四边形ABCD中,E为AD延长线上的一点,且BC=2DE,BE交DC于点F.若CF=2,则DF的长为1.
3.如图,在△ABC中,AB=AC=6,D为AC上一点,连接BD,且BD=BC=4,则DC=.
4.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是5.
5.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=2时,△ABC∽△DEF.
二、选择题
6.下列两个三角形不相似的是(
B
)
A.一个三角形的两个角分别是40°,80°;另一个三角形的两个角分别是60°,80°
B.一个三角形的三边长分别是4
cm,6
cm,8
cm;另一个三角形的三边长分别是12
cm,18
cm,21
cm
C.一个三角形的两边长分别是2
cm和5
cm,夹角是40°;另一个三角形的两边长分别是3
cm和7.5
cm,夹角是40°
D.各有一个角是120°的两个等腰三角形
7.如图,已知∠DAB=∠CAE,那么添加下列一个条件后,仍然无法判定△ABC∽△ADE的是(
A
)
A.=
B.=
C.∠B=∠D
D.∠C=∠AED
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为(
C
)
A.
B.
C.
D.
9.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
C
)
A.F
B.G
C.H
D.K
三、解答题
10.如图,四边形ABCD的对角形AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.
又∵∠AEB=∠DAE+∠ADE,
∠ADC=∠BDC+∠ADE,
∠DAE=∠BDC,
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
11.如图,已知==,求证:△ABD∽△ACE.
证明:∵==,
∴△ABC∽△ADE.
∴∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
又∵=,即=,
∴△ABD∽△ACE.
B组(中档题)
四、填空题
12.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则EF=3.
13.如图,△ABC中,AD1=AB,D1D2=D1B,D2D3=D2B,…,照这样继续下去,D2
020D2
021=D2
020B,且D1E1∥BC,D2E2∥BC,D2E3∥BC;…,D2
021E2
021∥BC,则=1-()2_021.
五、解答题
14.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM交DB于点N.
(1)求证:BD2=AD·CD.
(2)若CD=6,AD=8,则MN=.
解:证明:∵DB平分∠ADC,
∴∠ADB=∠BDC.
又∵∠ABD=∠BCD=90°,
∴△ABD∽△BCD.
∴=.
∴BD2=AD·CD.
C组(综合题)
15.如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是AE=AF.
(2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
解:(2)AF=kAE.
证明:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠ADF=90°.
∴∠FAD+∠FAB=90°.
∵AF⊥AE,∴∠EAF=90°.
∴∠EAB+∠FAB=90°.∴∠EAB=∠FAD.
∵∠ABE+∠ABC=180°,
∴∠ABE=180°-∠ABC=180°-90°=90°.
∴∠ABE=∠ADF.∴△ABE∽△ADF.
∴=.
∵AD=kAB,∴AF=kAE.
(3)①如图3,当点F在线段DC上时,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∵AD=2AB=4,∴AB=2.∴CD=2.
∵CF=1,∴DF=CD-CF=2-1=1.
在Rt△ADF中,∠ADF=90°,
∴AF===.
∵DF∥AB,∴∠GDF=∠GBA,∠GFD=∠GAB.
∴△GDF∽△GBA.∴==.
∵AF=GF+AG,∴AG=AF=.
由(2)得△ABE∽△ADF,∴===.
∴AE=AF=×=.
在Rt△EAG中,∠EAG=90°,
∴EG===.
②如图4,当点F在线段DC的延长线上时,DF=CD+CF=2+1=3,
在Rt△ADF中,∠ADF=90°,
∴AF===5.
∵DF∥AB,∴∠GAB=∠GFD,∠GBA=∠GDF.
∴△AGB∽△FGD.∴==.
∵GF+AG=AF=5,∴AG=2.
由(2)得△ABE∽△ADF,
∴===.
∴AE=AF=×5=.
在Rt△EAG中,∠EAG=90°,
∴EG===.
综上所述,EG的长为或.
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图,在△ABC中,若DE∥BC,DE=9
cm,BC=12
cm,则=_____.
2.如图,在平行四边形ABCD中,E为AD延长线上的一点,且BC=2DE,BE交DC于点F.若CF=2,则DF的长为_____.
3.如图,在△ABC中,AB=AC=6,D为AC上一点,连接BD,且BD=BC=4,则DC=_____.
4.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是_____.
5.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=_____时,△ABC∽△DEF.
二、选择题
6.下列两个三角形不相似的是(
)
A.一个三角形的两个角分别是40°,80°;另一个三角形的两个角分别是60°,80°
B.一个三角形的三边长分别是4
cm,6
cm,8
cm;另一个三角形的三边长分别是12
cm,18
cm,21
cm
C.一个三角形的两边长分别是2
cm和5
cm,夹角是40°;另一个三角形的两边长分别是3
cm和7.5
cm,夹角是40°
D.各有一个角是120°的两个等腰三角形
7.如图,已知∠DAB=∠CAE,那么添加下列一个条件后,仍然无法判定△ABC∽△ADE的是(
)
A.=
B.=
C.∠B=∠D
D.∠C=∠AED
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为(
)
A.
B.
C.
D.
9.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
)
A.F
B.G
C.H
D.K
三、解答题
10.如图,四边形ABCD的对角形AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
11.如图,已知==,求证:△ABD∽△ACE.
B组(中档题)
四、填空题
12.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则EF=_____.
13.如图,△ABC中,AD1=AB,D1D2=D1B,D2D3=D2B,…,照这样继续下去,D2
020D2
021=D2
020B,且D1E1∥BC,D2E2∥BC,D2E3∥BC;…,D2
021E2
021∥BC,则=_____.
五、解答题
14.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM交DB于点N.
(1)求证:BD2=AD·CD.
(2)若CD=6,AD=8,则MN=.
C组(综合题)
15.如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是_____.
(2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
参考答案
4.4探索三角形相似的条件同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图,在△ABC中,若DE∥BC,DE=9
cm,BC=12
cm,则=3.
2.如图,在平行四边形ABCD中,E为AD延长线上的一点,且BC=2DE,BE交DC于点F.若CF=2,则DF的长为1.
3.如图,在△ABC中,AB=AC=6,D为AC上一点,连接BD,且BD=BC=4,则DC=.
4.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是5.
5.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=2时,△ABC∽△DEF.
二、选择题
6.下列两个三角形不相似的是(
B
)
A.一个三角形的两个角分别是40°,80°;另一个三角形的两个角分别是60°,80°
B.一个三角形的三边长分别是4
cm,6
cm,8
cm;另一个三角形的三边长分别是12
cm,18
cm,21
cm
C.一个三角形的两边长分别是2
cm和5
cm,夹角是40°;另一个三角形的两边长分别是3
cm和7.5
cm,夹角是40°
D.各有一个角是120°的两个等腰三角形
7.如图,已知∠DAB=∠CAE,那么添加下列一个条件后,仍然无法判定△ABC∽△ADE的是(
A
)
A.=
B.=
C.∠B=∠D
D.∠C=∠AED
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则的值为(
C
)
A.
B.
C.
D.
9.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
C
)
A.F
B.G
C.H
D.K
三、解答题
10.如图,四边形ABCD的对角形AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.
又∵∠AEB=∠DAE+∠ADE,
∠ADC=∠BDC+∠ADE,
∠DAE=∠BDC,
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
11.如图,已知==,求证:△ABD∽△ACE.
证明:∵==,
∴△ABC∽△ADE.
∴∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
又∵=,即=,
∴△ABD∽△ACE.
B组(中档题)
四、填空题
12.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则EF=3.
13.如图,△ABC中,AD1=AB,D1D2=D1B,D2D3=D2B,…,照这样继续下去,D2
020D2
021=D2
020B,且D1E1∥BC,D2E2∥BC,D2E3∥BC;…,D2
021E2
021∥BC,则=1-()2_021.
五、解答题
14.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM交DB于点N.
(1)求证:BD2=AD·CD.
(2)若CD=6,AD=8,则MN=.
解:证明:∵DB平分∠ADC,
∴∠ADB=∠BDC.
又∵∠ABD=∠BCD=90°,
∴△ABD∽△BCD.
∴=.
∴BD2=AD·CD.
C组(综合题)
15.如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是AE=AF.
(2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
(3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
解:(2)AF=kAE.
证明:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠ADF=90°.
∴∠FAD+∠FAB=90°.
∵AF⊥AE,∴∠EAF=90°.
∴∠EAB+∠FAB=90°.∴∠EAB=∠FAD.
∵∠ABE+∠ABC=180°,
∴∠ABE=180°-∠ABC=180°-90°=90°.
∴∠ABE=∠ADF.∴△ABE∽△ADF.
∴=.
∵AD=kAB,∴AF=kAE.
(3)①如图3,当点F在线段DC上时,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∵AD=2AB=4,∴AB=2.∴CD=2.
∵CF=1,∴DF=CD-CF=2-1=1.
在Rt△ADF中,∠ADF=90°,
∴AF===.
∵DF∥AB,∴∠GDF=∠GBA,∠GFD=∠GAB.
∴△GDF∽△GBA.∴==.
∵AF=GF+AG,∴AG=AF=.
由(2)得△ABE∽△ADF,∴===.
∴AE=AF=×=.
在Rt△EAG中,∠EAG=90°,
∴EG===.
②如图4,当点F在线段DC的延长线上时,DF=CD+CF=2+1=3,
在Rt△ADF中,∠ADF=90°,
∴AF===5.
∵DF∥AB,∴∠GAB=∠GFD,∠GBA=∠GDF.
∴△AGB∽△FGD.∴==.
∵GF+AG=AF=5,∴AG=2.
由(2)得△ABE∽△ADF,
∴===.
∴AE=AF=×5=.
在Rt△EAG中,∠EAG=90°,
∴EG===.
综上所述,EG的长为或.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
