4.4.2两边成比例且夹角相等的判定方法同步练习题 2021-20 22学年北师大版九年级数学上册(word版含答案)
文档属性
| 名称 | 4.4.2两边成比例且夹角相等的判定方法同步练习题 2021-20 22学年北师大版九年级数学上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 139.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览



文档简介
4.4.2两边成比例且夹角相等的判定方法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.在△ABC和△A′B′C′中,若∠B=∠B′,AB=6,BC=8,B′C′=4,则当A′B′=___时,△ABC∽△A′B′C′.
2.在△ABC和△DEF中,∠A=∠D=105°,AC=4
cm,AB=6
cm,DE=3
cm,则DF=______时,△ABC与△DEF相似.
3.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是______.
4.如图,BD,CE交于点A,已知AB·AD=AC·AE,∠B=30°,则∠E=______.
5.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B,D的对应点为A,C,那么线段CE的长应等于______.
二、选择题
6.如图,△ABC与下列哪一个三角形相似(
)
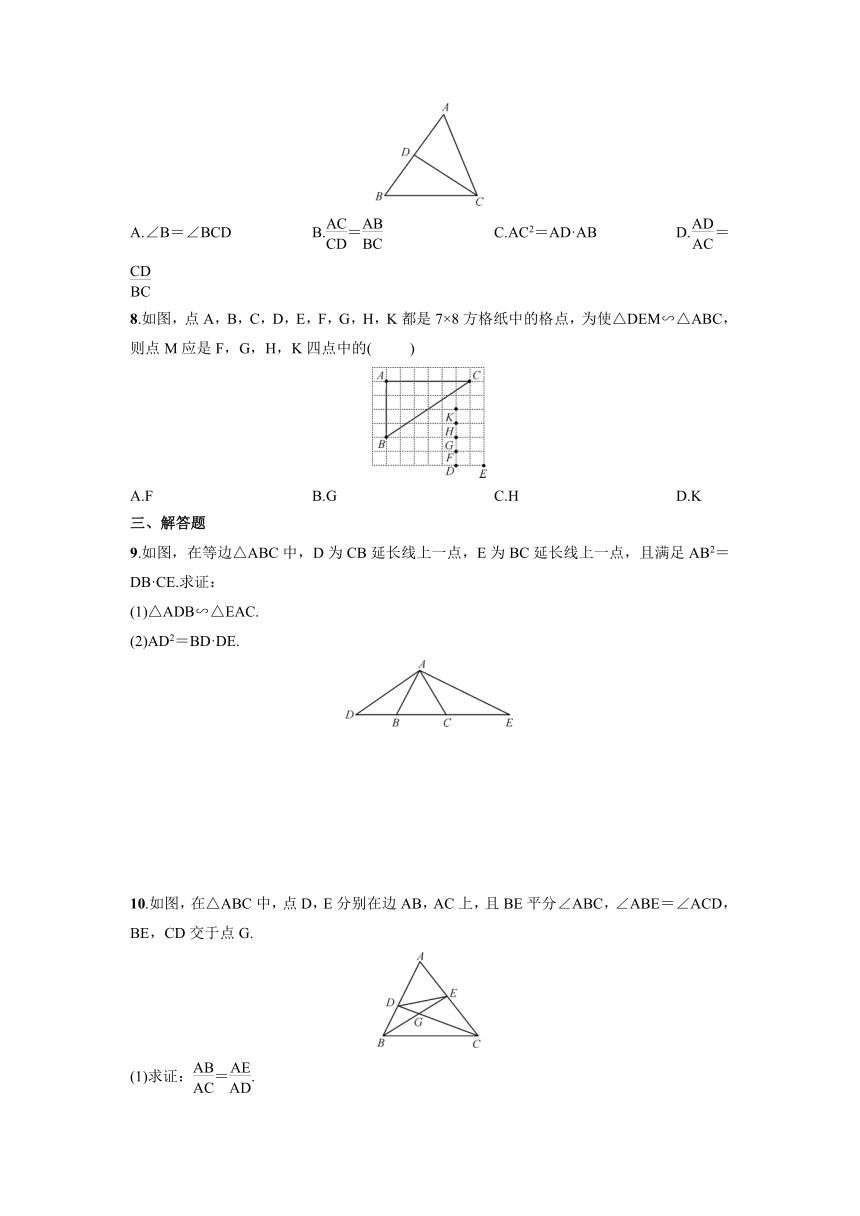
7.如图所示,给出下列哪个条件单独能够判定△ABC∽△ACD的是(
)
A.∠B=∠BCD
B.=
C.AC2=AD·AB
D.=
8.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
)
A.F
B.G
C.H
D.K
三、解答题
9.如图,在等边△ABC中,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:
(1)△ADB∽△EAC.
(2)AD2=BD·DE.
10.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=.
(2)连接DE,求证:DE=CE.
B组(中档题)
四、填空题
11.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=______时,以A,D,E为顶点的三角形与△ABC相似.
12.如图,在Rt△ABC中,∠C=90°,AC=6
cm,BC=8
cm,动点P从点B出发,在BA边上以5
cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4
cm/s的速度向点B匀速运动,运动时间为t
s(0<t<2),连接PQ.若以B,P,Q为顶点的三角形与△ABC相似,则t的值为______.
13.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=4,AC=3,AB=a,在线段AB上找一点E,使△BDE与△ACE相似.若这样的点E有且只有两个,则a的值是______.
五、解答题
14.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC.
(2)求证:△ACE∽△ABD.
(3)若CD=2CE,则CE=______.
C组(综合题)
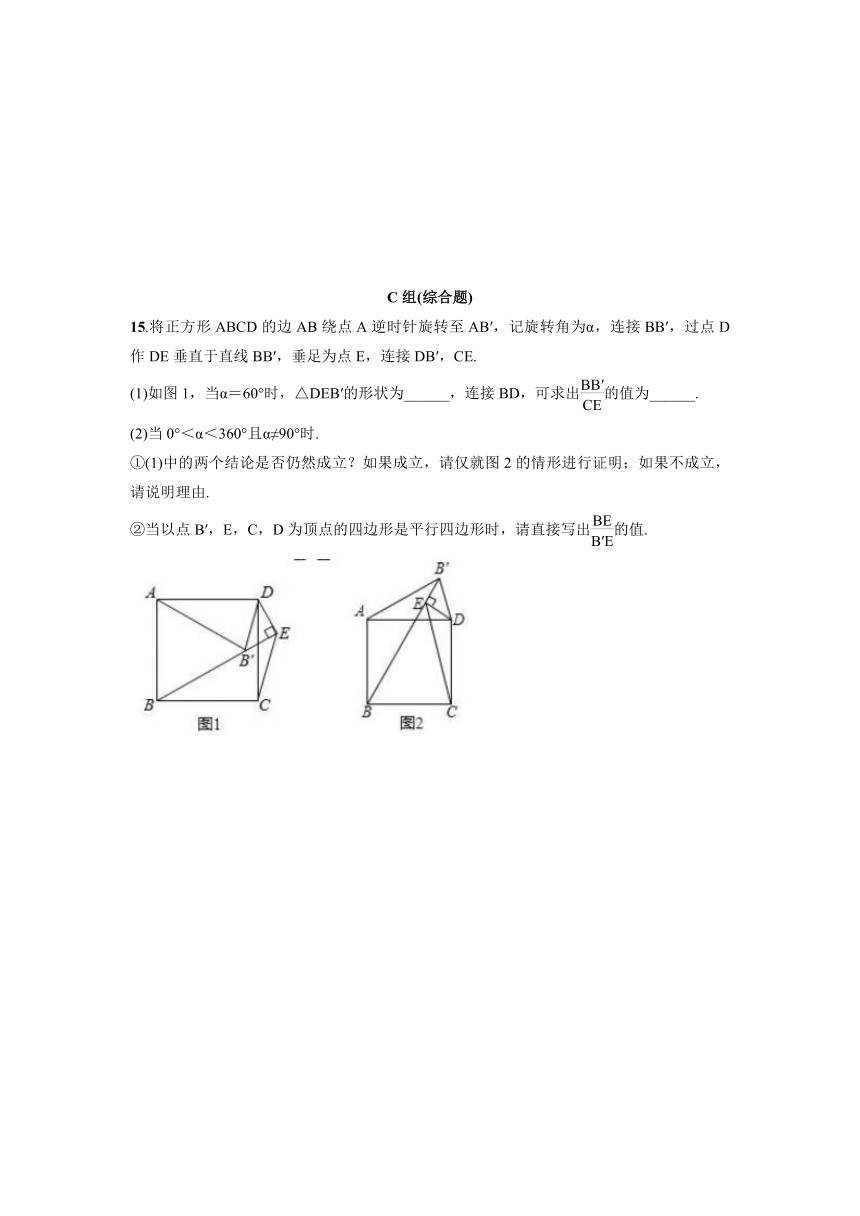
15.将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.
(1)如图1,当α=60°时,△DEB′的形状为______,连接BD,可求出的值为______.
(2)当0°<α<360°且α≠90°时.
①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由.
②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.
参考答案
4.4.2两边成比例且夹角相等的判定方法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.在△ABC和△A′B′C′中,若∠B=∠B′,AB=6,BC=8,B′C′=4,则当A′B′=3时,△ABC∽△A′B′C′.
2.在△ABC和△DEF中,∠A=∠D=105°,AC=4
cm,AB=6
cm,DE=3
cm,则DF=2_cm或_cm时,△ABC与△DEF相似.
3.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是1.8.
4.如图,BD,CE交于点A,已知AB·AD=AC·AE,∠B=30°,则∠E=30°.
5.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B,D的对应点为A,C,那么线段CE的长应等于.
二、选择题
6.如图,△ABC与下列哪一个三角形相似(
D
)
7.如图所示,给出下列哪个条件单独能够判定△ABC∽△ACD的是(
C
)
A.∠B=∠BCD
B.=
C.AC2=AD·AB
D.=
8.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
C
)
A.F
B.G
C.H
D.K
三、解答题
9.如图,在等边△ABC中,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:
(1)△ADB∽△EAC.
(2)AD2=BD·DE.
证明:(1)∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=AC.
∴∠DBA=∠ECA=120°.
∵AB2=DB·CE,
∴=.∴=.
∴△ADB∽△EAC.
(2)∵△ADB∽△EAC,
∴∠DAB=∠E.
又∵∠D=∠D,
∴△ADB∽△EDA.
∴=.
∴AD2=BD·DE.
10.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=.
(2)连接DE,求证:DE=CE.
证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD.
∴=.
(2)∵=,
∴=.
又∵∠A=∠A,
∴△ADE∽△ACB.
∴∠AED=∠ABC.
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE.
∵∠ABE=∠ACD,∴∠CDE=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE.
∴∠CDE=∠ABE=∠ACD.
∴DE=CE.
B组(中档题)
四、填空题
11.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=或时,以A,D,E为顶点的三角形与△ABC相似.
12.如图,在Rt△ABC中,∠C=90°,AC=6
cm,BC=8
cm,动点P从点B出发,在BA边上以5
cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4
cm/s的速度向点B匀速运动,运动时间为t
s(0<t<2),连接PQ.若以B,P,Q为顶点的三角形与△ABC相似,则t的值为1或.
13.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=4,AC=3,AB=a,在线段AB上找一点E,使△BDE与△ACE相似.若这样的点E有且只有两个,则a的值是7或4.
五、解答题
14.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC.
(2)求证:△ACE∽△ABD.
(3)若CD=2CE,则CE=16-8.
解:(1)证明:∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°.
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE.
∴△ADE∽△ABC.
(2)证明:∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°-∠CAD.
∵△ADE∽△ABC,
∴=.
∴=.
∴△ACE∽△ABD.
C组(综合题)
15.将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.
(1)如图1,当α=60°时,△DEB′的形状为等腰直角三角形,连接BD,可求出的值为.
(2)当0°<α<360°且α≠90°时.
①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由.
②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.
解:(2)①两结论仍然成立.
证明:连接BD,
∵AB=AB′,∠BAB′=α,∴∠AB′B=90°-.
∵∠B′AD=α-90°,AD=AB′,∴∠AB′D=135°-.
∴∠EB′D=∠AB′D-∠AB′B=135°--(90°-)=45°.
∵DE⊥BB′,∴∠EDB′=∠EB′D=45°.
∴△DEB′是等腰直角三角形.∴=.
∵四边形ABCD是正方形,
∴=,∠BDC=45°.∴=.
∵∠EDB′=∠BDC,
∴∠EDB′+∠EDB=∠BDC+∠EDB.
即∠B′DB=∠EDC.∴△B′DB∽△EDC.
∴==.
②=3或1.
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.在△ABC和△A′B′C′中,若∠B=∠B′,AB=6,BC=8,B′C′=4,则当A′B′=___时,△ABC∽△A′B′C′.
2.在△ABC和△DEF中,∠A=∠D=105°,AC=4
cm,AB=6
cm,DE=3
cm,则DF=______时,△ABC与△DEF相似.
3.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是______.
4.如图,BD,CE交于点A,已知AB·AD=AC·AE,∠B=30°,则∠E=______.
5.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B,D的对应点为A,C,那么线段CE的长应等于______.
二、选择题
6.如图,△ABC与下列哪一个三角形相似(
)
7.如图所示,给出下列哪个条件单独能够判定△ABC∽△ACD的是(
)
A.∠B=∠BCD
B.=
C.AC2=AD·AB
D.=
8.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
)
A.F
B.G
C.H
D.K
三、解答题
9.如图,在等边△ABC中,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:
(1)△ADB∽△EAC.
(2)AD2=BD·DE.
10.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=.
(2)连接DE,求证:DE=CE.
B组(中档题)
四、填空题
11.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=______时,以A,D,E为顶点的三角形与△ABC相似.
12.如图,在Rt△ABC中,∠C=90°,AC=6
cm,BC=8
cm,动点P从点B出发,在BA边上以5
cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4
cm/s的速度向点B匀速运动,运动时间为t
s(0<t<2),连接PQ.若以B,P,Q为顶点的三角形与△ABC相似,则t的值为______.
13.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=4,AC=3,AB=a,在线段AB上找一点E,使△BDE与△ACE相似.若这样的点E有且只有两个,则a的值是______.
五、解答题
14.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC.
(2)求证:△ACE∽△ABD.
(3)若CD=2CE,则CE=______.
C组(综合题)
15.将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.
(1)如图1,当α=60°时,△DEB′的形状为______,连接BD,可求出的值为______.
(2)当0°<α<360°且α≠90°时.
①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由.
②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.
参考答案
4.4.2两边成比例且夹角相等的判定方法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.在△ABC和△A′B′C′中,若∠B=∠B′,AB=6,BC=8,B′C′=4,则当A′B′=3时,△ABC∽△A′B′C′.
2.在△ABC和△DEF中,∠A=∠D=105°,AC=4
cm,AB=6
cm,DE=3
cm,则DF=2_cm或_cm时,△ABC与△DEF相似.
3.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是1.8.
4.如图,BD,CE交于点A,已知AB·AD=AC·AE,∠B=30°,则∠E=30°.
5.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B,D的对应点为A,C,那么线段CE的长应等于.
二、选择题
6.如图,△ABC与下列哪一个三角形相似(
D
)
7.如图所示,给出下列哪个条件单独能够判定△ABC∽△ACD的是(
C
)
A.∠B=∠BCD
B.=
C.AC2=AD·AB
D.=
8.如图,点A,B,C,D,E,F,G,H,K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的(
C
)
A.F
B.G
C.H
D.K
三、解答题
9.如图,在等边△ABC中,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:
(1)△ADB∽△EAC.
(2)AD2=BD·DE.
证明:(1)∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=AC.
∴∠DBA=∠ECA=120°.
∵AB2=DB·CE,
∴=.∴=.
∴△ADB∽△EAC.
(2)∵△ADB∽△EAC,
∴∠DAB=∠E.
又∵∠D=∠D,
∴△ADB∽△EDA.
∴=.
∴AD2=BD·DE.
10.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=.
(2)连接DE,求证:DE=CE.
证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD.
∴=.
(2)∵=,
∴=.
又∵∠A=∠A,
∴△ADE∽△ACB.
∴∠AED=∠ABC.
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE.
∵∠ABE=∠ACD,∴∠CDE=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE.
∴∠CDE=∠ABE=∠ACD.
∴DE=CE.
B组(中档题)
四、填空题
11.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=或时,以A,D,E为顶点的三角形与△ABC相似.
12.如图,在Rt△ABC中,∠C=90°,AC=6
cm,BC=8
cm,动点P从点B出发,在BA边上以5
cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4
cm/s的速度向点B匀速运动,运动时间为t
s(0<t<2),连接PQ.若以B,P,Q为顶点的三角形与△ABC相似,则t的值为1或.
13.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=4,AC=3,AB=a,在线段AB上找一点E,使△BDE与△ACE相似.若这样的点E有且只有两个,则a的值是7或4.
五、解答题
14.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC.
(2)求证:△ACE∽△ABD.
(3)若CD=2CE,则CE=16-8.
解:(1)证明:∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°.
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE.
∴△ADE∽△ABC.
(2)证明:∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°-∠CAD.
∵△ADE∽△ABC,
∴=.
∴=.
∴△ACE∽△ABD.
C组(综合题)
15.将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.
(1)如图1,当α=60°时,△DEB′的形状为等腰直角三角形,连接BD,可求出的值为.
(2)当0°<α<360°且α≠90°时.
①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由.
②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.
解:(2)①两结论仍然成立.
证明:连接BD,
∵AB=AB′,∠BAB′=α,∴∠AB′B=90°-.
∵∠B′AD=α-90°,AD=AB′,∴∠AB′D=135°-.
∴∠EB′D=∠AB′D-∠AB′B=135°--(90°-)=45°.
∵DE⊥BB′,∴∠EDB′=∠EB′D=45°.
∴△DEB′是等腰直角三角形.∴=.
∵四边形ABCD是正方形,
∴=,∠BDC=45°.∴=.
∵∠EDB′=∠BDC,
∴∠EDB′+∠EDB=∠BDC+∠EDB.
即∠B′DB=∠EDC.∴△B′DB∽△EDC.
∴==.
②=3或1.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
