4.4.3三边成比例的判定方法同步练习题 2021-2022学年北师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 4.4.3三边成比例的判定方法同步练习题 2021-2022学年北师大版九年级数学上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览



文档简介
4.4.3三边成比例的判定方法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知△ABC的三边长分别为,,2,△A′B′C′的两边长分别是1和,当△A′B′C′的第三边长为_____时,△ABC与△A′B′C′相似.
2.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=_____时,△ABC∽△DEF.
3.如图,在边长为1的正方形网格中有点P,A,B,C,则图中所形成的三角形中,相似的三角形是_____.
二、选择题
4.甲三角形的三边分别为1,,,乙三角形的三边分别为,,5,则甲、乙两个三角形(
)
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断是否相似
5.下列数据分别表示两个三角形的三边长,则两个三角形相似的是(
)
A.2,4,5与4,9,12
B.3,5,7与,,
C.3,2,4与9,12,6
D.2.5,5,4与0.5,1.1,1.5
6.在下列条件中,不能判断△ABC与△DEF相似的是(
)
A.∠A=∠D,∠B=∠E
B.=且∠B=∠E
C.==
D.=且∠A=∠D
7.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是(
)
三、解答题
8.如图,在△ABC中,AB=2,AC=2,BC=4.在△DEF中,DE=3,DF=3,EF=6.求证:△ABC∽△DEF.
9.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,方格纸中小方格是边长为1的正方形,试判断格点图形△ABC与△DEF是否相似,并说明你的理由.
B组(中档题)
四、填空题
10.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在_____处(填序号),能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似.
11.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有_____个.
12.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是_____.
五、解答题
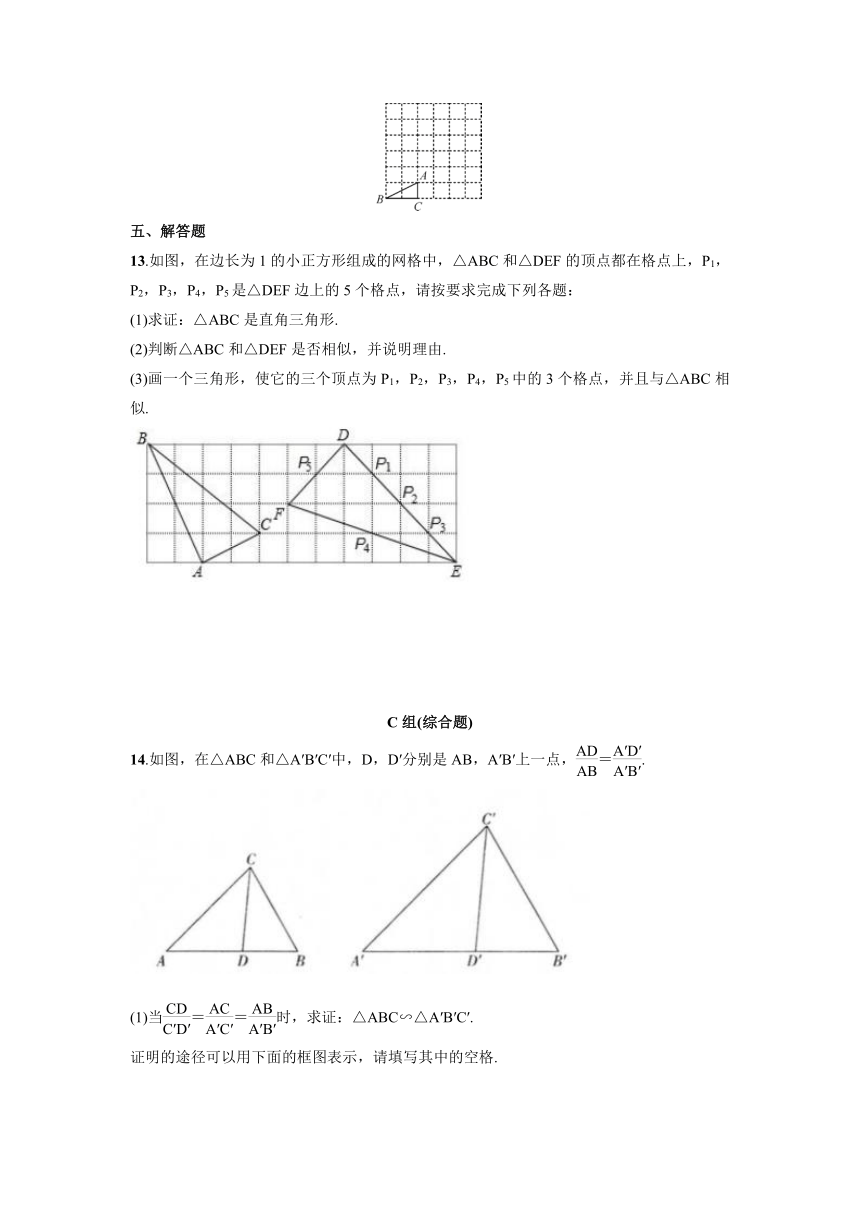
13.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)求证:△ABC是直角三角形.
(2)判断△ABC和△DEF是否相似,并说明理由.
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点,并且与△ABC相似.
C组(综合题)
14.如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.
(1)当==时,求证:△ABC∽△A′B′C′.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
参考答案
4.4.3三边成比例的判定方法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知△ABC的三边长分别为,,2,△A′B′C′的两边长分别是1和,当△A′B′C′的第三边长为时,△ABC与△A′B′C′相似.
2.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=2时,△ABC∽△DEF.
3.如图,在边长为1的正方形网格中有点P,A,B,C,则图中所形成的三角形中,相似的三角形是△APB∽△CPA.
二、选择题
4.甲三角形的三边分别为1,,,乙三角形的三边分别为,,5,则甲、乙两个三角形(A)
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断是否相似
5.下列数据分别表示两个三角形的三边长,则两个三角形相似的是(
C
)
A.2,4,5与4,9,12
B.3,5,7与,,
C.3,2,4与9,12,6
D.2.5,5,4与0.5,1.1,1.5
6.在下列条件中,不能判断△ABC与△DEF相似的是(
B
)
A.∠A=∠D,∠B=∠E
B.=且∠B=∠E
C.==
D.=且∠A=∠D
7.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是(
B
)
三、解答题
8.如图,在△ABC中,AB=2,AC=2,BC=4.在△DEF中,DE=3,DF=3,EF=6.求证:△ABC∽△DEF.
证明:∵==,==,==,
∴==.
∴△ABC∽△DEF.
9.在方格纸中,每个小方格的顶点叫做格点,以格点连线为边的图形叫做格点图形.如图,方格纸中小方格是边长为1的正方形,试判断格点图形△ABC与△DEF是否相似,并说明你的理由.
解:△ABC与△DEF相似.理由如下:
由小方格是边长为1的正方形,根据勾股定理易求得:
DE=,DF=2,EF=,AB=,AC=,BC=5.
∴===.
∴△ABC∽△DEF.
B组(中档题)
四、填空题
10.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在②处(填序号),能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似.
11.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有6个.
12.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是5.
五、解答题
13.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)求证:△ABC是直角三角形.
(2)判断△ABC和△DEF是否相似,并说明理由.
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点,并且与△ABC相似.
解:(1)证明:根据勾股定理,得AB=2,AC=,BC=5,则AB2+AC2=BC2,
∴△ABC为直角三角形.
(2)△ABC和△DEF相似.理由:
根据勾股定理,得AB=2,AC=,BC=5,
DE=4,DF=2,EF=2.
∴===.
∴△ABC∽△DEF.
(3)如图,△P2P4P5即为所作.
C组(综合题)
14.如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.
(1)当==时,求证:△ABC∽△A′B′C′.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
解:(1)== ∠A=∠A′
(2)相似.过点D,D′分别作DE∥BC,D′E′∥B′C′,DE交AC于E,D′E′交A′C′于E′.
∵DE∥BC,∴△ADE∽△ABC.
∴==.同理,==,
∵=,∴=.
∴=.同理,=.
∴=,即=.
∴=.
∵==.
∴==.
∴△DCE∽△D′C′E′.
∴∠CED=∠C′E′D′.
∵DE∥BC,∴∠CED+∠ACB=180°.
同理∠C′E′D′+∠A′C′B′=180°.
∴∠ACB=∠A′C′B′.
∵=,
∴△ABC∽△A′B′C′.
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知△ABC的三边长分别为,,2,△A′B′C′的两边长分别是1和,当△A′B′C′的第三边长为_____时,△ABC与△A′B′C′相似.
2.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=_____时,△ABC∽△DEF.
3.如图,在边长为1的正方形网格中有点P,A,B,C,则图中所形成的三角形中,相似的三角形是_____.
二、选择题
4.甲三角形的三边分别为1,,,乙三角形的三边分别为,,5,则甲、乙两个三角形(
)
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断是否相似
5.下列数据分别表示两个三角形的三边长,则两个三角形相似的是(
)
A.2,4,5与4,9,12
B.3,5,7与,,
C.3,2,4与9,12,6
D.2.5,5,4与0.5,1.1,1.5
6.在下列条件中,不能判断△ABC与△DEF相似的是(
)
A.∠A=∠D,∠B=∠E
B.=且∠B=∠E
C.==
D.=且∠A=∠D
7.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是(
)
三、解答题
8.如图,在△ABC中,AB=2,AC=2,BC=4.在△DEF中,DE=3,DF=3,EF=6.求证:△ABC∽△DEF.
9.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,方格纸中小方格是边长为1的正方形,试判断格点图形△ABC与△DEF是否相似,并说明你的理由.
B组(中档题)
四、填空题
10.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在_____处(填序号),能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似.
11.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有_____个.
12.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是_____.
五、解答题
13.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)求证:△ABC是直角三角形.
(2)判断△ABC和△DEF是否相似,并说明理由.
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点,并且与△ABC相似.
C组(综合题)
14.如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.
(1)当==时,求证:△ABC∽△A′B′C′.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
参考答案
4.4.3三边成比例的判定方法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知△ABC的三边长分别为,,2,△A′B′C′的两边长分别是1和,当△A′B′C′的第三边长为时,△ABC与△A′B′C′相似.
2.在△ABC中AB=8,AC=6,在△DEF中,DE=4,DF=3,当=2时,△ABC∽△DEF.
3.如图,在边长为1的正方形网格中有点P,A,B,C,则图中所形成的三角形中,相似的三角形是△APB∽△CPA.
二、选择题
4.甲三角形的三边分别为1,,,乙三角形的三边分别为,,5,则甲、乙两个三角形(A)
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断是否相似
5.下列数据分别表示两个三角形的三边长,则两个三角形相似的是(
C
)
A.2,4,5与4,9,12
B.3,5,7与,,
C.3,2,4与9,12,6
D.2.5,5,4与0.5,1.1,1.5
6.在下列条件中,不能判断△ABC与△DEF相似的是(
B
)
A.∠A=∠D,∠B=∠E
B.=且∠B=∠E
C.==
D.=且∠A=∠D
7.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是(
B
)
三、解答题
8.如图,在△ABC中,AB=2,AC=2,BC=4.在△DEF中,DE=3,DF=3,EF=6.求证:△ABC∽△DEF.
证明:∵==,==,==,
∴==.
∴△ABC∽△DEF.
9.在方格纸中,每个小方格的顶点叫做格点,以格点连线为边的图形叫做格点图形.如图,方格纸中小方格是边长为1的正方形,试判断格点图形△ABC与△DEF是否相似,并说明你的理由.
解:△ABC与△DEF相似.理由如下:
由小方格是边长为1的正方形,根据勾股定理易求得:
DE=,DF=2,EF=,AB=,AC=,BC=5.
∴===.
∴△ABC∽△DEF.
B组(中档题)
四、填空题
10.在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在②处(填序号),能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似.
11.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有6个.
12.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是5.
五、解答题
13.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)求证:△ABC是直角三角形.
(2)判断△ABC和△DEF是否相似,并说明理由.
(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点,并且与△ABC相似.
解:(1)证明:根据勾股定理,得AB=2,AC=,BC=5,则AB2+AC2=BC2,
∴△ABC为直角三角形.
(2)△ABC和△DEF相似.理由:
根据勾股定理,得AB=2,AC=,BC=5,
DE=4,DF=2,EF=2.
∴===.
∴△ABC∽△DEF.
(3)如图,△P2P4P5即为所作.
C组(综合题)
14.如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.
(1)当==时,求证:△ABC∽△A′B′C′.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
解:(1)== ∠A=∠A′
(2)相似.过点D,D′分别作DE∥BC,D′E′∥B′C′,DE交AC于E,D′E′交A′C′于E′.
∵DE∥BC,∴△ADE∽△ABC.
∴==.同理,==,
∵=,∴=.
∴=.同理,=.
∴=,即=.
∴=.
∵==.
∴==.
∴△DCE∽△D′C′E′.
∴∠CED=∠C′E′D′.
∵DE∥BC,∴∠CED+∠ACB=180°.
同理∠C′E′D′+∠A′C′B′=180°.
∴∠ACB=∠A′C′B′.
∵=,
∴△ABC∽△A′B′C′.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
