2021-202 学年北师大版九年级数学上册5.1.2平行投影同步练习题 (word含答案)
文档属性
| 名称 | 2021-202 学年北师大版九年级数学上册5.1.2平行投影同步练习题 (word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览

文档简介
5.1.2平行投影同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
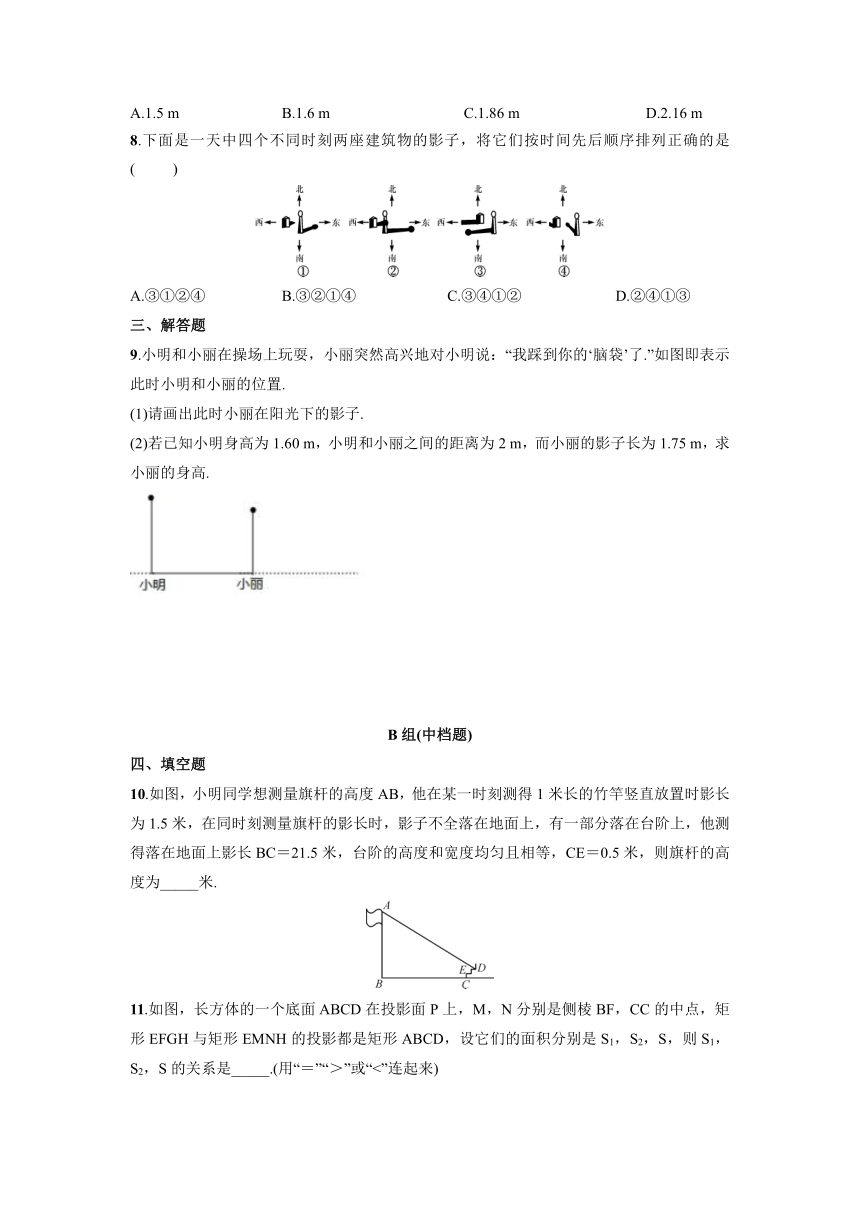
1.如图是两棵小树在同一时刻的影子,则图1是_____投影,图2是_____投影.
2.小亮在上午8时、9时、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为上午8时.
3.如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为_____米.
4.如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD为2米.若树脚到墙的距离BC为8米,则树高AB为_____米.
二、选择题
5.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是(
)
6.矩形的正投影不可能是(
)
A.线段
B.矩形
C.正方形
D.梯形
7.如图,某一时刻阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8
m,窗户下檐到地面的距离BC=1
m,EC=1.2
m,那么窗户的高AB为(
)
A.1.5
m
B.1.6
m
C.1.86
m
D.2.16
m
8.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序排列正确的是(
)
A.③①②④
B.③②①④
C.③④①②
D.②④①③
三、解答题
9.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子.
(2)若已知小明身高为1.60
m,小明和小丽之间的距离为2
m,而小丽的影子长为1.75
m,求小丽的身高.
B组(中档题)
四、填空题
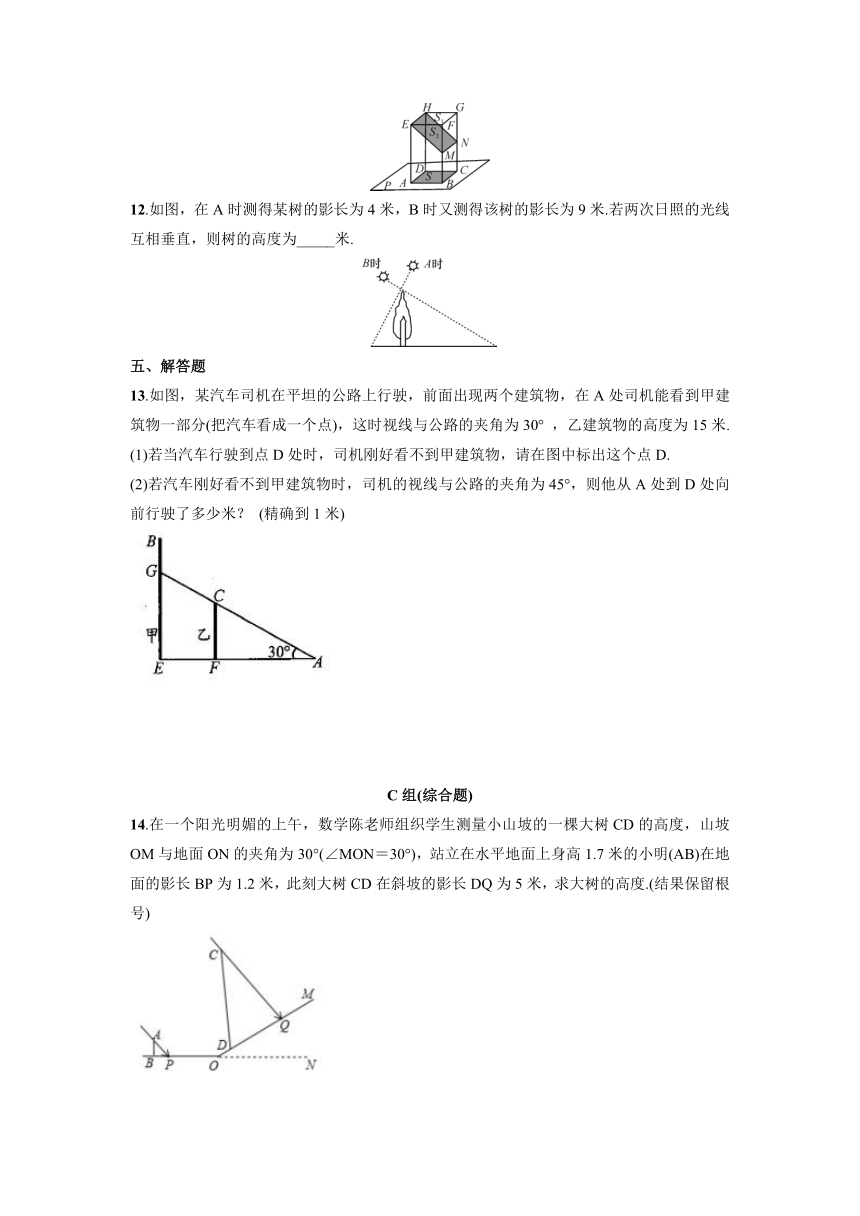
10.如图,小明同学想测量旗杆的高度AB,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同时刻测量旗杆的影长时,影子不全落在地面上,有一部分落在台阶上,他测得落在地面上影长BC=21.5米,台阶的高度和宽度均匀且相等,CE=0.5米,则旗杆的高度为_____米.
11.如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CC的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是_____.(用“=”“>”或“<”连起来)
12.如图,在A时测得某树的影长为4米,B时又测得该树的影长为9米.若两次日照的光线互相垂直,则树的高度为_____米.
五、解答题
13.如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路的夹角为30°
,乙建筑物的高度为15米.
(1)若当汽车行驶到点D处时,司机刚好看不到甲建筑物,请在图中标出这个点D.
(2)若汽车刚好看不到甲建筑物时,司机的视线与公路的夹角为45°,则他从A处到D处向前行驶了多少米?
(精确到1米)
C组(综合题)
14.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一棵大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明(AB)在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.(结果保留根号)
参考答案
5.1.2平行投影同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图是两棵小树在同一时刻的影子,则图1是平行投影,图2是中心投影.
2.小亮在上午8时、9时、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为上午8时.
3.如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为10米.
4.如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD为2米.若树脚到墙的距离BC为8米,则树高AB为10米.
二、选择题
5.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是(
C
)
6.矩形的正投影不可能是(
D
)
A.线段
B.矩形
C.正方形
D.梯形
7.如图,某一时刻阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8
m,窗户下檐到地面的距离BC=1
m,EC=1.2
m,那么窗户的高AB为(
A
)
A.1.5
m
B.1.6
m
C.1.86
m
D.2.16
m
8.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序排列正确的是(
C
)
A.③①②④
B.③②①④
C.③④①②
D.②④①③
三、解答题
9.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子.
(2)若已知小明身高为1.60
m,小明和小丽之间的距离为2
m,而小丽的影子长为1.75
m,求小丽的身高.
解:(1)如图所示,CA即为小丽在阳光下的影子.
(2)小明身高为1.60
m,小明和小丽之间的距离为2
m,而小丽的影子长为1.75
m,
设小丽的身高为x
m,则
=,
解得
x=1.4.
答:小丽的身高为1.4
m.
B组(中档题)
四、填空题
10.如图,小明同学想测量旗杆的高度AB,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同时刻测量旗杆的影长时,影子不全落在地面上,有一部分落在台阶上,他测得落在地面上影长BC=21.5米,台阶的高度和宽度均匀且相等,CE=0.5米,则旗杆的高度为16米.
11.如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CC的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是S1=S<S2.(用“=”“>”或“<”连起来)
12.如图,在A时测得某树的影长为4米,B时又测得该树的影长为9米.若两次日照的光线互相垂直,则树的高度为6米.
五、解答题
13.如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路的夹角为30°
,乙建筑物的高度为15米.
(1)若当汽车行驶到点D处时,司机刚好看不到甲建筑物,请在图中标出这个点D.
(2)若汽车刚好看不到甲建筑物时,司机的视线与公路的夹角为45°,则他从A处到D处向前行驶了多少米?
(精确到1米)
解:(1)如图所示,点D即为所求.
(2)由题意知∠CAF=30°,∠FDC=45°,CF=15米.
∴CA=30米,CF=DF=15米.
∴AF=15米.
∴AD=AF-DF=15-15≈11(米).
∴他从A到D向前行驶了11米.
C组(综合题)
14.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一棵大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明(AB)在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.(结果保留根号)
解:过点Q作QE⊥DC于点E,
由题意可得△ABP∽△CEQ,
则=,故=,
又∵EQ∥NO,
∴∠QON=∠OQE=30°.
∵QD=5
m,
∴DE=
m,EQ=
m.
∴=.
解得EC=.
∴CE+DE=+=(m).
答:大树的高度为
m.
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图是两棵小树在同一时刻的影子,则图1是_____投影,图2是_____投影.
2.小亮在上午8时、9时、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为上午8时.
3.如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为_____米.
4.如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD为2米.若树脚到墙的距离BC为8米,则树高AB为_____米.
二、选择题
5.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是(
)
6.矩形的正投影不可能是(
)
A.线段
B.矩形
C.正方形
D.梯形
7.如图,某一时刻阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8
m,窗户下檐到地面的距离BC=1
m,EC=1.2
m,那么窗户的高AB为(
)
A.1.5
m
B.1.6
m
C.1.86
m
D.2.16
m
8.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序排列正确的是(
)
A.③①②④
B.③②①④
C.③④①②
D.②④①③
三、解答题
9.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子.
(2)若已知小明身高为1.60
m,小明和小丽之间的距离为2
m,而小丽的影子长为1.75
m,求小丽的身高.
B组(中档题)
四、填空题
10.如图,小明同学想测量旗杆的高度AB,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同时刻测量旗杆的影长时,影子不全落在地面上,有一部分落在台阶上,他测得落在地面上影长BC=21.5米,台阶的高度和宽度均匀且相等,CE=0.5米,则旗杆的高度为_____米.
11.如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CC的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是_____.(用“=”“>”或“<”连起来)
12.如图,在A时测得某树的影长为4米,B时又测得该树的影长为9米.若两次日照的光线互相垂直,则树的高度为_____米.
五、解答题
13.如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路的夹角为30°
,乙建筑物的高度为15米.
(1)若当汽车行驶到点D处时,司机刚好看不到甲建筑物,请在图中标出这个点D.
(2)若汽车刚好看不到甲建筑物时,司机的视线与公路的夹角为45°,则他从A处到D处向前行驶了多少米?
(精确到1米)
C组(综合题)
14.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一棵大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明(AB)在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.(结果保留根号)
参考答案
5.1.2平行投影同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图是两棵小树在同一时刻的影子,则图1是平行投影,图2是中心投影.
2.小亮在上午8时、9时、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为上午8时.
3.如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为10米.
4.如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD为2米.若树脚到墙的距离BC为8米,则树高AB为10米.
二、选择题
5.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是(
C
)
6.矩形的正投影不可能是(
D
)
A.线段
B.矩形
C.正方形
D.梯形
7.如图,某一时刻阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8
m,窗户下檐到地面的距离BC=1
m,EC=1.2
m,那么窗户的高AB为(
A
)
A.1.5
m
B.1.6
m
C.1.86
m
D.2.16
m
8.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序排列正确的是(
C
)
A.③①②④
B.③②①④
C.③④①②
D.②④①③
三、解答题
9.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子.
(2)若已知小明身高为1.60
m,小明和小丽之间的距离为2
m,而小丽的影子长为1.75
m,求小丽的身高.
解:(1)如图所示,CA即为小丽在阳光下的影子.
(2)小明身高为1.60
m,小明和小丽之间的距离为2
m,而小丽的影子长为1.75
m,
设小丽的身高为x
m,则
=,
解得
x=1.4.
答:小丽的身高为1.4
m.
B组(中档题)
四、填空题
10.如图,小明同学想测量旗杆的高度AB,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同时刻测量旗杆的影长时,影子不全落在地面上,有一部分落在台阶上,他测得落在地面上影长BC=21.5米,台阶的高度和宽度均匀且相等,CE=0.5米,则旗杆的高度为16米.
11.如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CC的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是S1=S<S2.(用“=”“>”或“<”连起来)
12.如图,在A时测得某树的影长为4米,B时又测得该树的影长为9米.若两次日照的光线互相垂直,则树的高度为6米.
五、解答题
13.如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路的夹角为30°
,乙建筑物的高度为15米.
(1)若当汽车行驶到点D处时,司机刚好看不到甲建筑物,请在图中标出这个点D.
(2)若汽车刚好看不到甲建筑物时,司机的视线与公路的夹角为45°,则他从A处到D处向前行驶了多少米?
(精确到1米)
解:(1)如图所示,点D即为所求.
(2)由题意知∠CAF=30°,∠FDC=45°,CF=15米.
∴CA=30米,CF=DF=15米.
∴AF=15米.
∴AD=AF-DF=15-15≈11(米).
∴他从A到D向前行驶了11米.
C组(综合题)
14.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一棵大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明(AB)在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.(结果保留根号)
解:过点Q作QE⊥DC于点E,
由题意可得△ABP∽△CEQ,
则=,故=,
又∵EQ∥NO,
∴∠QON=∠OQE=30°.
∵QD=5
m,
∴DE=
m,EQ=
m.
∴=.
解得EC=.
∴CE+DE=+=(m).
答:大树的高度为
m.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
