4.8.1位似图形及其性质与画法同步练习题 2021-2022学年北师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 4.8.1位似图形及其性质与画法同步练习题 2021-2022学年北师大版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 210.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 08:44:57 | ||
图片预览



文档简介
4.8.1位似图形及其性质与画法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知,如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与△A′B′C′是位似图形,位似比为_____;△OAB与_____是位似图形,位似比为_____.
2.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形.若C1为OC的中点,AB=4,则A1B1的长为_____.
3.如图,O是正△PQR的中心,P′,Q′,R′分别是OP,OQ,OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似中心是点_____,相似比为_____.
4.如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=_____.
5.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是_____.
6.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为=.若五边形ABCDE的面积为15
cm2,那么五边形A′B′C′D′E′的面积为_____.
二、选择题
7.在△ABC中,AB=AC,∠A=36°.以点A为位似中心,把△ABC放大2倍后得△AB′C′,则∠B′=(
)
A.72°
B.54°
C.36°
D.144°
8.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,则以下说法中错误的是(
)
A.△ABC∽△A′B′C′
B.C,O,C′三点在同一直线上
C.AO∶AA′=1∶2
D.AB∥A′B′
9.如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为(
)
A.1∶2
B.1∶3
C.1∶4
D.1∶5
10.如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO∶AD的值为(
)
A.2∶3
B.2∶5
C.4∶9
D.4∶13
11.如图是△ABC位似图形的几种画法,其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
三、解答题
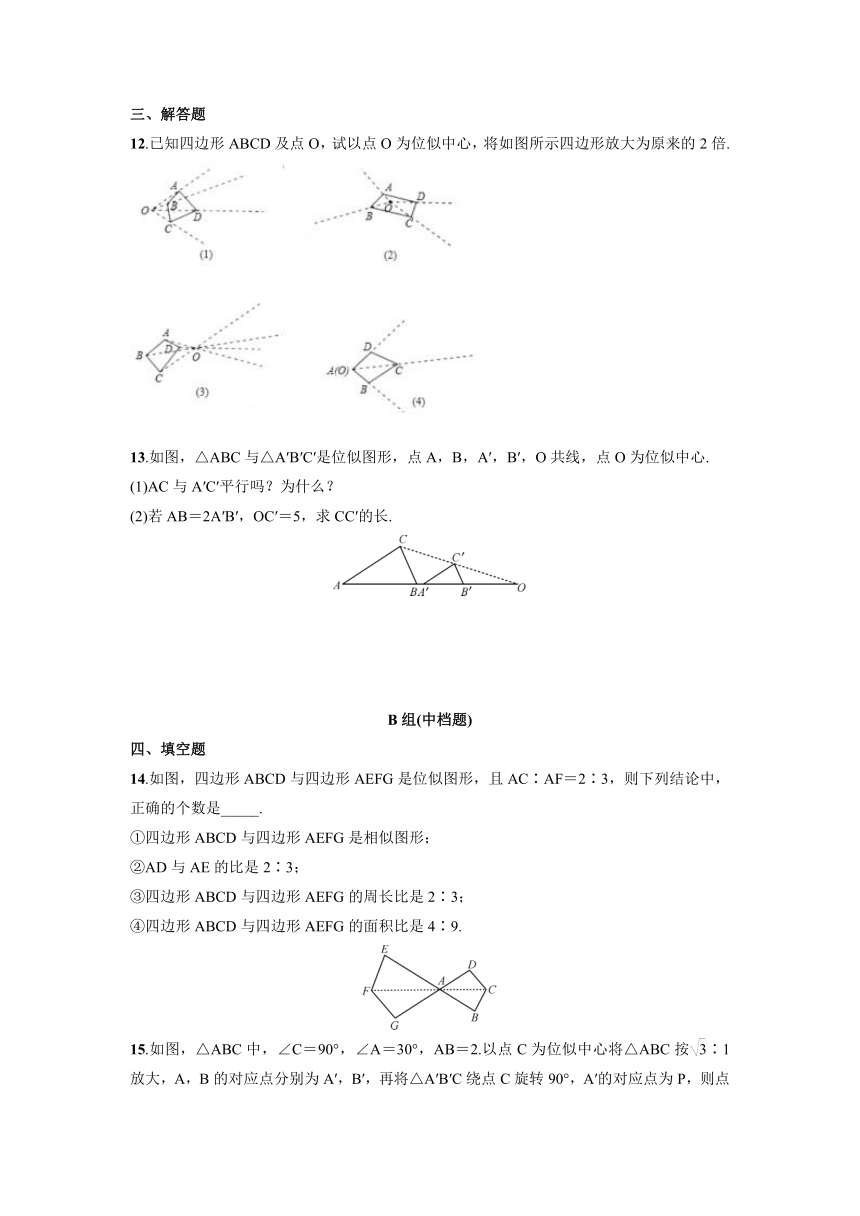
12.已知四边形ABCD及点O,试以点O为位似中心,将如图所示四边形放大为原来的2倍.
13.如图,△ABC与△A′B′C′是位似图形,点A,B,A′,B′,O共线,点O为位似中心.
(1)AC与A′C′平行吗?为什么?
(2)若AB=2A′B′,OC′=5,求CC′的长.
B组(中档题)
四、填空题
14.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论中,正确的个数是_____.
①四边形ABCD与四边形AEFG是相似图形;
②AD与AE的比是2∶3;
③四边形ABCD与四边形AEFG的周长比是2∶3;
④四边形ABCD与四边形AEFG的面积比是4∶9.
15.如图,△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按∶1放大,A,B的对应点分别为A′,B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为_____.
五、解答题
16.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′.
(2)若=3,S四边形BCDE=20,则S四边形B′C′D′E′=.
C组(综合题)
17.如图所示,由位似的等边△A1B1C1,等边△A2B2C2,等边△A3B3C3,…等边△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心.
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
参考答案
4.8.1位似图形及其性质与画法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知,如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与△A′B′C′是位似图形,位似比为7∶4;△OAB与△OA′B′是位似图形,位似比为7∶4.
2.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形.若C1为OC的中点,AB=4,则A1B1的长为2.
3.如图,O是正△PQR的中心,P′,Q′,R′分别是OP,OQ,OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似中心是点O,相似比为1∶2.
4.如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=.
5.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是1∶2.
6.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为=.若五边形ABCDE的面积为15
cm2,那么五边形A′B′C′D′E′的面积为_cm2.
二、选择题
7.在△ABC中,AB=AC,∠A=36°.以点A为位似中心,把△ABC放大2倍后得△AB′C′,则∠B′=(
A
)
A.72°
B.54°
C.36°
D.144°
8.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,则以下说法中错误的是(
C
)
A.△ABC∽△A′B′C′
B.C,O,C′三点在同一直线上
C.AO∶AA′=1∶2
D.AB∥A′B′
9.如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为(
C
)
A.1∶2
B.1∶3
C.1∶4
D.1∶5
10.如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO∶AD的值为(
B
)
A.2∶3
B.2∶5
C.4∶9
D.4∶13
11.如图是△ABC位似图形的几种画法,其中正确的有(
C
)
A.1个
B.2个
C.3个
D.4个
三、解答题
12.已知四边形ABCD及点O,试以点O为位似中心,将如图所示四边形放大为原来的2倍.
解:如图所示.
13.如图,△ABC与△A′B′C′是位似图形,点A,B,A′,B′,O共线,点O为位似中心.
(1)AC与A′C′平行吗?为什么?
(2)若AB=2A′B′,OC′=5,求CC′的长.
解:(1)AC∥A′C′.理由如下:
∵△ABC与△A′B′C′是位似图形,
∴△ABC∽△A′B′C′,
∴∠A=∠C′A′B′.
∴AC∥A′C′.
(2)∵△ABC∽△A′B′C′,
∴=.
∵AB=2A′B′,
∴==.
又∵△ABC与△A′B′C′是位似图形,
∴==.
∵OC′=5,
∴OC=10,
∴CC′=OC-OC′=10-5=5.
B组(中档题)
四、填空题
14.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论中,正确的个数是3.
①四边形ABCD与四边形AEFG是相似图形;
②AD与AE的比是2∶3;
③四边形ABCD与四边形AEFG的周长比是2∶3;
④四边形ABCD与四边形AEFG的面积比是4∶9.
15.如图,△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按∶1放大,A,B的对应点分别为A′,B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.
五、解答题
16.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′.
(2)若=3,S四边形BCDE=20,则S四边形B′C′D′E′=.
证明:∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴=====.
又∵四边形BCDE与四边形B′C′D′E′对应顶点的连线相交于一点A,
∴四边形BCDE位似于四边形B′C′D′E′.
C组(综合题)
17.如图所示,由位似的等边△A1B1C1,等边△A2B2C2,等边△A3B3C3,…等边△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心.
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
解:(1)∵△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,
∴等边△A2B2C2的边长为.
等边△A3B3C3的边长为()2.
……
等边△A10B10C10和的边长为()9,等边△A7B7C7的边长为()6.
∴等边△A10B10C10和等边△A7B7C7的相似比==;
它们的位似中心仍为点O.
(2)∵第n个三角形△AnBnCn(n≥2)的边长为()n-1,
∴第n个三角形△AnBnCn(n≥2)的周长为.
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知,如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与△A′B′C′是位似图形,位似比为_____;△OAB与_____是位似图形,位似比为_____.
2.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形.若C1为OC的中点,AB=4,则A1B1的长为_____.
3.如图,O是正△PQR的中心,P′,Q′,R′分别是OP,OQ,OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似中心是点_____,相似比为_____.
4.如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=_____.
5.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是_____.
6.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为=.若五边形ABCDE的面积为15
cm2,那么五边形A′B′C′D′E′的面积为_____.
二、选择题
7.在△ABC中,AB=AC,∠A=36°.以点A为位似中心,把△ABC放大2倍后得△AB′C′,则∠B′=(
)
A.72°
B.54°
C.36°
D.144°
8.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,则以下说法中错误的是(
)
A.△ABC∽△A′B′C′
B.C,O,C′三点在同一直线上
C.AO∶AA′=1∶2
D.AB∥A′B′
9.如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为(
)
A.1∶2
B.1∶3
C.1∶4
D.1∶5
10.如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO∶AD的值为(
)
A.2∶3
B.2∶5
C.4∶9
D.4∶13
11.如图是△ABC位似图形的几种画法,其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
三、解答题
12.已知四边形ABCD及点O,试以点O为位似中心,将如图所示四边形放大为原来的2倍.
13.如图,△ABC与△A′B′C′是位似图形,点A,B,A′,B′,O共线,点O为位似中心.
(1)AC与A′C′平行吗?为什么?
(2)若AB=2A′B′,OC′=5,求CC′的长.
B组(中档题)
四、填空题
14.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论中,正确的个数是_____.
①四边形ABCD与四边形AEFG是相似图形;
②AD与AE的比是2∶3;
③四边形ABCD与四边形AEFG的周长比是2∶3;
④四边形ABCD与四边形AEFG的面积比是4∶9.
15.如图,△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按∶1放大,A,B的对应点分别为A′,B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为_____.
五、解答题
16.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′.
(2)若=3,S四边形BCDE=20,则S四边形B′C′D′E′=.
C组(综合题)
17.如图所示,由位似的等边△A1B1C1,等边△A2B2C2,等边△A3B3C3,…等边△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心.
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
参考答案
4.8.1位似图形及其性质与画法同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.已知,如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与△A′B′C′是位似图形,位似比为7∶4;△OAB与△OA′B′是位似图形,位似比为7∶4.
2.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形.若C1为OC的中点,AB=4,则A1B1的长为2.
3.如图,O是正△PQR的中心,P′,Q′,R′分别是OP,OQ,OR的中点,则△P′Q′R′与△PQR是位似三角形,此时△P′Q′R′与△PQR的位似中心是点O,相似比为1∶2.
4.如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=.
5.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是1∶2.
6.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为=.若五边形ABCDE的面积为15
cm2,那么五边形A′B′C′D′E′的面积为_cm2.
二、选择题
7.在△ABC中,AB=AC,∠A=36°.以点A为位似中心,把△ABC放大2倍后得△AB′C′,则∠B′=(
A
)
A.72°
B.54°
C.36°
D.144°
8.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,则以下说法中错误的是(
C
)
A.△ABC∽△A′B′C′
B.C,O,C′三点在同一直线上
C.AO∶AA′=1∶2
D.AB∥A′B′
9.如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为(
C
)
A.1∶2
B.1∶3
C.1∶4
D.1∶5
10.如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO∶AD的值为(
B
)
A.2∶3
B.2∶5
C.4∶9
D.4∶13
11.如图是△ABC位似图形的几种画法,其中正确的有(
C
)
A.1个
B.2个
C.3个
D.4个
三、解答题
12.已知四边形ABCD及点O,试以点O为位似中心,将如图所示四边形放大为原来的2倍.
解:如图所示.
13.如图,△ABC与△A′B′C′是位似图形,点A,B,A′,B′,O共线,点O为位似中心.
(1)AC与A′C′平行吗?为什么?
(2)若AB=2A′B′,OC′=5,求CC′的长.
解:(1)AC∥A′C′.理由如下:
∵△ABC与△A′B′C′是位似图形,
∴△ABC∽△A′B′C′,
∴∠A=∠C′A′B′.
∴AC∥A′C′.
(2)∵△ABC∽△A′B′C′,
∴=.
∵AB=2A′B′,
∴==.
又∵△ABC与△A′B′C′是位似图形,
∴==.
∵OC′=5,
∴OC=10,
∴CC′=OC-OC′=10-5=5.
B组(中档题)
四、填空题
14.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论中,正确的个数是3.
①四边形ABCD与四边形AEFG是相似图形;
②AD与AE的比是2∶3;
③四边形ABCD与四边形AEFG的周长比是2∶3;
④四边形ABCD与四边形AEFG的面积比是4∶9.
15.如图,△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按∶1放大,A,B的对应点分别为A′,B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.
五、解答题
16.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′.
(2)若=3,S四边形BCDE=20,则S四边形B′C′D′E′=.
证明:∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴=====.
又∵四边形BCDE与四边形B′C′D′E′对应顶点的连线相交于一点A,
∴四边形BCDE位似于四边形B′C′D′E′.
C组(综合题)
17.如图所示,由位似的等边△A1B1C1,等边△A2B2C2,等边△A3B3C3,…等边△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn,C2,C3,…,Cn都在B1C1边上.
(1)试写出△A10B10C10和△A7B7C7的相似比和位似中心.
(2)求出第n个三角形△AnBnCn(n≥2)的周长.
解:(1)∵△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,
∴等边△A2B2C2的边长为.
等边△A3B3C3的边长为()2.
……
等边△A10B10C10和的边长为()9,等边△A7B7C7的边长为()6.
∴等边△A10B10C10和等边△A7B7C7的相似比==;
它们的位似中心仍为点O.
(2)∵第n个三角形△AnBnCn(n≥2)的边长为()n-1,
∴第n个三角形△AnBnCn(n≥2)的周长为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
