2021-2022学年北师大版九年级数学上册第四章图形的相似单元同步练习题(Word版,含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册第四章图形的相似单元同步练习题(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 103.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 21:47:41 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学上册第四章
图形的相似
单元同步练习题
A组(基础题)
一、填空题
1.已知△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,那么△ABC与△A2B2C2的相似比为_____.
2.已知===k,则直线y=kx+2k一定经过第_____象限.
3.如图,在△ABC中,EF∥BC,AB=3AE.若S四边形BCFE=16,则S△ABC=_____.
4.如图,在?ABCD中,点E在AB边上,连接CE,BD交于点F.若AE∶BE=4∶3,BF=3,则BD=_____.
5.如图,路灯O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米.若同学们测得他在该路灯下的影长AC为2米,则路灯到地面的距离为_____米.
二、选择题
6.如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,EF=2,则(
)
A.BC∶DE=1∶2
B.BC∶DE=2∶3
C.BC∶DE=3∶2
D.BC·DE=6
7.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比恰好为黄金比.已知这本书的长为20
cm,则它的宽约为(
)
A.32.36
cm
B.13.6
cm
C.12.36
cm
D.7.64
cm
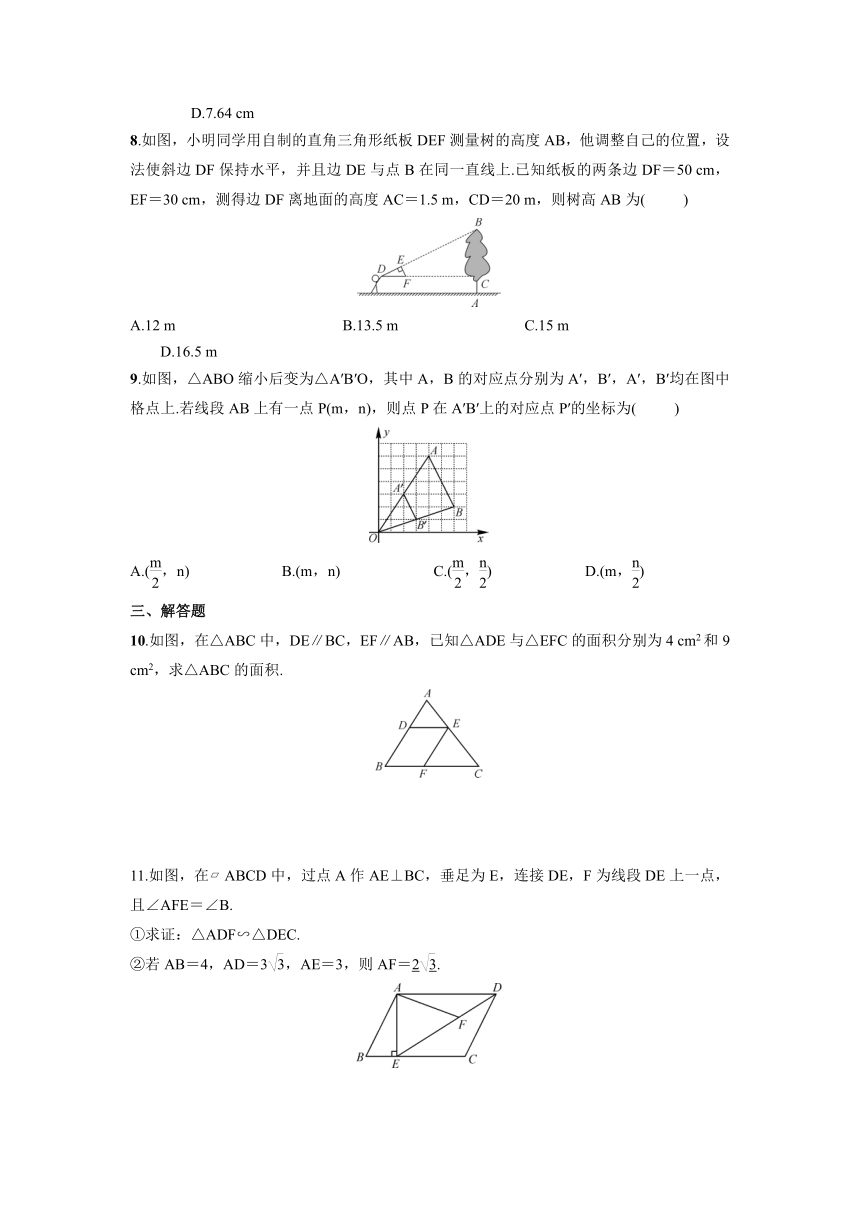
8.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50
cm,EF=30
cm,测得边DF离地面的高度AC=1.5
m,CD=20
m,则树高AB为(
)
A.12
m
B.13.5
m
C.15
m
D.16.5
m
9.如图,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,A′,B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为(
)
A.(,n)
B.(m,n)
C.(,)
D.(m,)
三、解答题
10.如图,在△ABC中,DE∥BC,EF∥AB,已知△ADE与△EFC的面积分别为4
cm2和9
cm2,求△ABC的面积.
11.如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
①求证:△ADF∽△DEC.
②若AB=4,AD=3,AE=3,则AF=2.
B组(中档题)
四、填空题
12.如图,在?ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,设△AGH的面积为S1,?ABCD的面积为S2,则S1∶S2的值为.
13.将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4.若以点B′,F,C为顶点的三角形与△ABC相似,则BF的长度是_____.
14.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是
_____.
五、解答题
15.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC,BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF.
(2)如图2,在∠EDF绕点D旋转的过程中,探究三条线段AB,CE,CF之间的数量关系,并说明理由.
C组(综合题)
16.(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:=.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长为_____.
②如图3,求证:MN2=DM·EN.
参考答案
2021-2022学年北师大版九年级数学上册第四章
图形的相似
单元同步练习题
A组(基础题)
一、填空题
1.已知△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,那么△ABC与△A2B2C2的相似比为2∶5.
2.已知===k,则直线y=kx+2k一定经过第二、三象限.
3.如图,在△ABC中,EF∥BC,AB=3AE.若S四边形BCFE=16,则S△ABC=18.
4.如图,在?ABCD中,点E在AB边上,连接CE,BD交于点F.若AE∶BE=4∶3,BF=3,则BD=10.
5.如图,路灯O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米.若同学们测得他在该路灯下的影长AC为2米,则路灯到地面的距离为4.8米.
二、选择题
6.如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,EF=2,则(
D
)
A.BC∶DE=1∶2
B.BC∶DE=2∶3
C.BC∶DE=3∶2
D.BC·DE=6
7.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比恰好为黄金比.已知这本书的长为20
cm,则它的宽约为(
C
)
A.32.36
cm
B.13.6
cm
C.12.36
cm
D.7.64
cm
8.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50
cm,EF=30
cm,测得边DF离地面的高度AC=1.5
m,CD=20
m,则树高AB为(
D
)
A.12
m
B.13.5
m
C.15
m
D.16.5
m
9.如图,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,A′,B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为(
C
)
A.(,n)
B.(m,n)
C.(,)
D.(m,)
三、解答题
10.如图,在△ABC中,DE∥BC,EF∥AB,已知△ADE与△EFC的面积分别为4
cm2和9
cm2,求△ABC的面积.
解:∵DE∥BC,EF∥AB,
∴∠C=∠AED,∠FEC=∠A,∠ADE=∠B.
∴△ADE∽△EFC,△ADE∽△ABC,
∴=()2,=()2.
∵又S△ADE=4
cm2,S△EFC=9
cm2.
∴()2=.
∴=.
∴()2=()2.
∴S△ABC=4÷=25(cm)2.
11.如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
①求证:△ADF∽△DEC.
②若AB=4,AD=3,AE=3,则AF=2.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
B组(中档题)
四、填空题
12.如图,在?ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,设△AGH的面积为S1,?ABCD的面积为S2,则S1∶S2的值为.
13.将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4.若以点B′,F,C为顶点的三角形与△ABC相似,则BF的长度是或2.
14.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是.
五、解答题
15.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC,BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF.
(2)如图2,在∠EDF绕点D旋转的过程中,探究三条线段AB,CE,CF之间的数量关系,并说明理由.
解:(1)证明:∵∠ACB=90°,AC=BC,AD=BD,
∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°.
∴∠DCE=∠DCF=135°.
在△DCE和△DCF中,
∴△DCE≌△DCF.
∴DE=DF.
(2)∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°-135°=45°.
∵∠CDF+∠CDE=45°,
∴∠F=∠CDE.
∴△CDF∽△CED.
∴=.
∴CD2=CE·CF.
∵∠ACB=90°,AD=BD,
∴CD=AB.
∴AB2=4CE·CF.
C组(综合题)
16.(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:=.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长为.
②如图3,求证:MN2=DM·EN.
解:(1)证明:在△ABQ和△ADP中,
∵DP∥BQ,
∴△ADP∽△ABQ.
∴=.
同理在△ACQ和△AEP中,=.
∴=.
(2)②证明:∵∠B+∠C=90°,∠CEF+∠C=90°,
∴∠B=∠CEF.
又∵∠BGD=∠EFC,
∴△BGD∽△EFC.
∴=.
∴DG·EF=CF·BG.
又∵DG=GF=EF,
∴GF2=CF·BG.
由(1)得==.
∴·=·.
∴()2=·.
∵GF2=CF·BG,
∴MN2=DM·EN.
图形的相似
单元同步练习题
A组(基础题)
一、填空题
1.已知△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,那么△ABC与△A2B2C2的相似比为_____.
2.已知===k,则直线y=kx+2k一定经过第_____象限.
3.如图,在△ABC中,EF∥BC,AB=3AE.若S四边形BCFE=16,则S△ABC=_____.
4.如图,在?ABCD中,点E在AB边上,连接CE,BD交于点F.若AE∶BE=4∶3,BF=3,则BD=_____.
5.如图,路灯O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米.若同学们测得他在该路灯下的影长AC为2米,则路灯到地面的距离为_____米.
二、选择题
6.如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,EF=2,则(
)
A.BC∶DE=1∶2
B.BC∶DE=2∶3
C.BC∶DE=3∶2
D.BC·DE=6
7.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比恰好为黄金比.已知这本书的长为20
cm,则它的宽约为(
)
A.32.36
cm
B.13.6
cm
C.12.36
cm
D.7.64
cm
8.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50
cm,EF=30
cm,测得边DF离地面的高度AC=1.5
m,CD=20
m,则树高AB为(
)
A.12
m
B.13.5
m
C.15
m
D.16.5
m
9.如图,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,A′,B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为(
)
A.(,n)
B.(m,n)
C.(,)
D.(m,)
三、解答题
10.如图,在△ABC中,DE∥BC,EF∥AB,已知△ADE与△EFC的面积分别为4
cm2和9
cm2,求△ABC的面积.
11.如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
①求证:△ADF∽△DEC.
②若AB=4,AD=3,AE=3,则AF=2.
B组(中档题)
四、填空题
12.如图,在?ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,设△AGH的面积为S1,?ABCD的面积为S2,则S1∶S2的值为.
13.将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4.若以点B′,F,C为顶点的三角形与△ABC相似,则BF的长度是_____.
14.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是
_____.
五、解答题
15.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC,BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF.
(2)如图2,在∠EDF绕点D旋转的过程中,探究三条线段AB,CE,CF之间的数量关系,并说明理由.
C组(综合题)
16.(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:=.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长为_____.
②如图3,求证:MN2=DM·EN.
参考答案
2021-2022学年北师大版九年级数学上册第四章
图形的相似
单元同步练习题
A组(基础题)
一、填空题
1.已知△ABC与△A1B1C1的相似比为2∶3,△A1B1C1与△A2B2C2的相似比为3∶5,那么△ABC与△A2B2C2的相似比为2∶5.
2.已知===k,则直线y=kx+2k一定经过第二、三象限.
3.如图,在△ABC中,EF∥BC,AB=3AE.若S四边形BCFE=16,则S△ABC=18.
4.如图,在?ABCD中,点E在AB边上,连接CE,BD交于点F.若AE∶BE=4∶3,BF=3,则BD=10.
5.如图,路灯O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米.若同学们测得他在该路灯下的影长AC为2米,则路灯到地面的距离为4.8米.
二、选择题
6.如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,EF=2,则(
D
)
A.BC∶DE=1∶2
B.BC∶DE=2∶3
C.BC∶DE=3∶2
D.BC·DE=6
7.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比恰好为黄金比.已知这本书的长为20
cm,则它的宽约为(
C
)
A.32.36
cm
B.13.6
cm
C.12.36
cm
D.7.64
cm
8.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50
cm,EF=30
cm,测得边DF离地面的高度AC=1.5
m,CD=20
m,则树高AB为(
D
)
A.12
m
B.13.5
m
C.15
m
D.16.5
m
9.如图,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,A′,B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为(
C
)
A.(,n)
B.(m,n)
C.(,)
D.(m,)
三、解答题
10.如图,在△ABC中,DE∥BC,EF∥AB,已知△ADE与△EFC的面积分别为4
cm2和9
cm2,求△ABC的面积.
解:∵DE∥BC,EF∥AB,
∴∠C=∠AED,∠FEC=∠A,∠ADE=∠B.
∴△ADE∽△EFC,△ADE∽△ABC,
∴=()2,=()2.
∵又S△ADE=4
cm2,S△EFC=9
cm2.
∴()2=.
∴=.
∴()2=()2.
∴S△ABC=4÷=25(cm)2.
11.如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
①求证:△ADF∽△DEC.
②若AB=4,AD=3,AE=3,则AF=2.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
B组(中档题)
四、填空题
12.如图,在?ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,设△AGH的面积为S1,?ABCD的面积为S2,则S1∶S2的值为.
13.将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4.若以点B′,F,C为顶点的三角形与△ABC相似,则BF的长度是或2.
14.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是.
五、解答题
15.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC,BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF.
(2)如图2,在∠EDF绕点D旋转的过程中,探究三条线段AB,CE,CF之间的数量关系,并说明理由.
解:(1)证明:∵∠ACB=90°,AC=BC,AD=BD,
∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°.
∴∠DCE=∠DCF=135°.
在△DCE和△DCF中,
∴△DCE≌△DCF.
∴DE=DF.
(2)∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°-135°=45°.
∵∠CDF+∠CDE=45°,
∴∠F=∠CDE.
∴△CDF∽△CED.
∴=.
∴CD2=CE·CF.
∵∠ACB=90°,AD=BD,
∴CD=AB.
∴AB2=4CE·CF.
C组(综合题)
16.(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:=.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长为.
②如图3,求证:MN2=DM·EN.
解:(1)证明:在△ABQ和△ADP中,
∵DP∥BQ,
∴△ADP∽△ABQ.
∴=.
同理在△ACQ和△AEP中,=.
∴=.
(2)②证明:∵∠B+∠C=90°,∠CEF+∠C=90°,
∴∠B=∠CEF.
又∵∠BGD=∠EFC,
∴△BGD∽△EFC.
∴=.
∴DG·EF=CF·BG.
又∵DG=GF=EF,
∴GF2=CF·BG.
由(1)得==.
∴·=·.
∴()2=·.
∵GF2=CF·BG,
∴MN2=DM·EN.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
