6.2.2分层随机抽样第一课时 课件(共21张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册(共21张PPT)
文档属性
| 名称 | 6.2.2分层随机抽样第一课时 课件(共21张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 45.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
6.2.2分层随机抽样
北师大(2019)必修1
第一课时
复习回顾
简单随机抽样特点是什么?
①总体容量较小;
②逐个抽取;
③不放回抽取;
④每个个体被抽到的机会相等
情境设置
那么当总体中的个体有很大差异时,适宜采用什么抽取方法?
问题1:全国各地的人口和住户的基本情况相同吗?
不同,有很大的差异
问题2:如果用简单随机抽样或系统抽样来抽取,样本具有代表性吗?
不具有代表性
提出问题
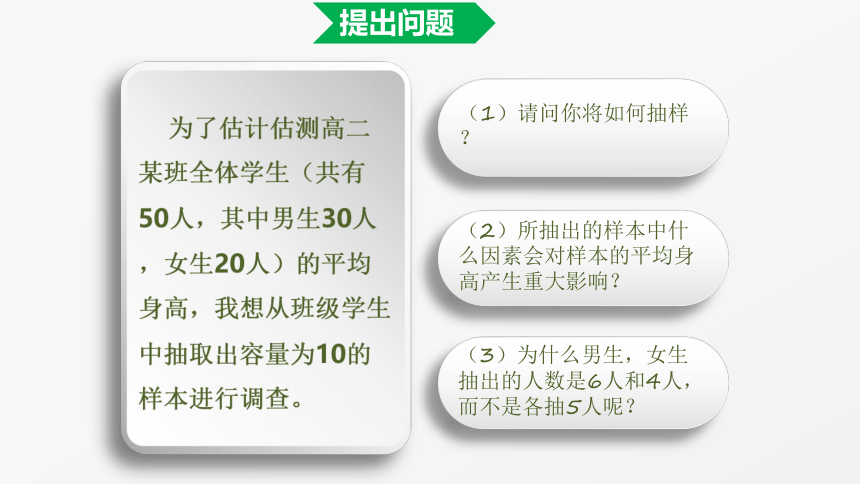
为了估计估测高二某班全体学生(共有50人,其中男生30人,女生20人)的平均身高,我想从班级学生中抽取出容量为10的样本进行调查。
提出问题
(1)请问你将如何抽样?
(2)所抽出的样本中什么因素会对样本的平均身高产生重大影响?
(3)为什么男生,女生抽出的人数是6人和4人,而不是各抽5人呢?
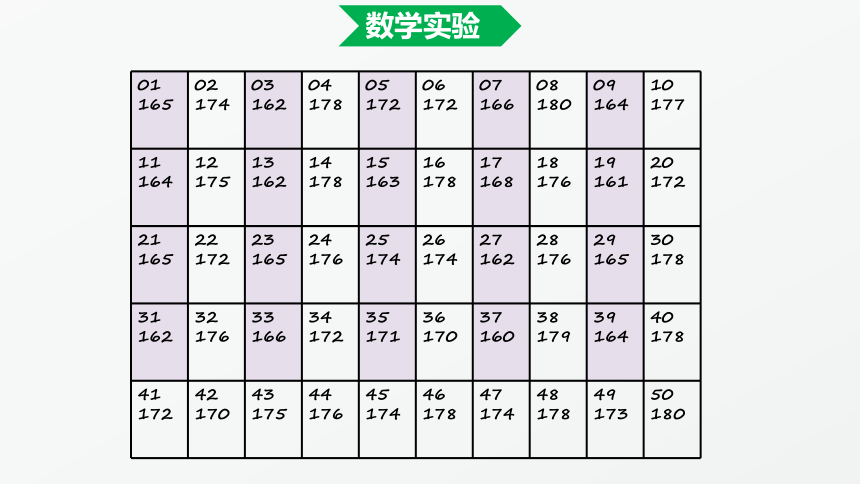
数学实验
01
165
02
174
03
162
04
178
05
172
06
172
07
166
08
180
09
164
10
177
11
164
12
175
13
162
14
178
15
163
16
178
17
168
18
176
19
161
20
172
21
165
22
172
23
165
24
176
25
174
26
174
27
162
28
176
29
165
30
178
31
162
32
176
33
166
34
172
35
171
36
170
37
160
38
179
39
164
40
178
41
172
42
170
43
175
44
176
45
174
46
178
47
174
48
178
49
173
50
180
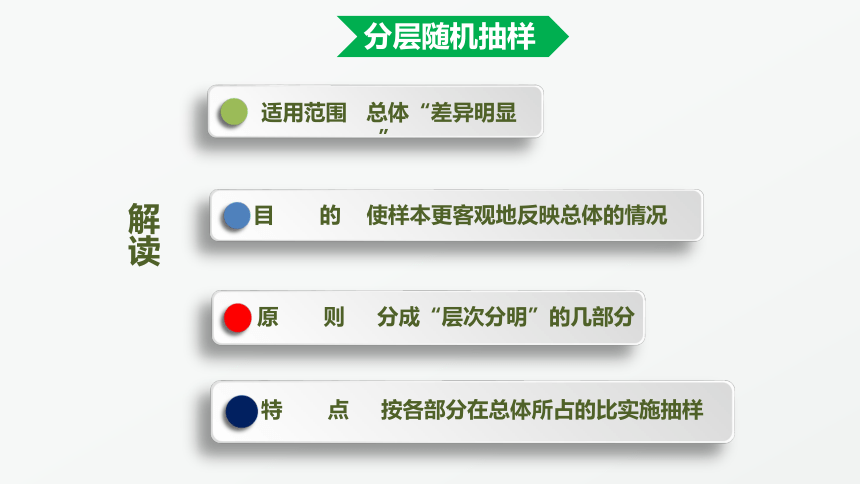
分层随机抽样
将总体按其属性特征分成互不交叉的若干类型(有时称作层),然后在每个类型中按照所占比例随机抽取一定的个体,这种抽样方法通常叫作分层随机抽样
分层随机抽样
解读
适用范围
总体“差异明显”
目
的
使样本更客观地反映总体的情况
原
则
分成“层次分明”的几部分
特
点
按各部分在总体所占的比实施抽样
分层随机抽样步骤
(1)将总体按一定的标准分层(分层)
(2)计算各层的个体数与总体的个体数的比(定比)
(3)按各层个体数与总体的个体数的比确定各层应抽取的样本容量(定量)
(4)在每一层进行抽样(抽样)
分层随机抽样思辨
判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)分层随机抽样适用于总体由差异明显的几部分组成,而层内个体间无明显差异的抽样.(
√
)
(2)在分层随机抽样中,各层抽取的个体数相等.(
×
)
(3)用分层随机抽样的方法,在分层时,每层的各个个体互不交叉,既不重复,又不遗漏.(
√
)
(4)在分层随机抽样中,每个个体被抽到的可能性是相等的,与层数及分层无关.(
√
)
?
?
?
?
分层随机抽样思辨
下列问题中,采用怎样的抽样方法较为合理?
(1)从10台冰箱中抽取3台进行质量检查;
(2)某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名.为了了解教职工对校务公开方面的意见,拟抽取一个容量为20的样本.
简单随机抽样法
分层随机抽样法
分层随机抽样应用
例1.某电视台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如表所示
很喜爱
喜爱
一般
不喜欢
2435
4567
3926
1072
电视台为进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应怎样进行抽样?
分析:人数多,差异大→分层随机抽样→确定每层抽取的比例→在各层中分别抽取→合在一起得样本
解:采用分层随机抽样的方法,抽样比为.
持“很喜爱”态度的有2
435人,应抽取2
435×≈12(人);
持“喜爱”态度的有4
567人,应抽取4
567×≈23(人);
持“一般”态度的有3
926人,应抽取3
926×≈20(人);
持“不喜爱”态度的有1
072人,应抽取1
072×≈5(人).
因此,采用分层随机抽样的方法在持“很喜爱”“喜爱”“一般”
“不喜爱”态度的人中分别抽取12人、23人、20人和5人.
解题心得
在分层随机抽样的过程中,为了保证每个个体被抽到的可能性是相等的,要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比.
分层随机抽样应用
例2.
某学校有在编人员200人,其中行政人员20人,教师140人,后勤人员40人.教育部门为了解学校职工对学校县管校聘改革的意见,要从中抽取20人,试确定用何种方法抽样,并写出抽样过程.
解:(1)将200人分成行政人员、教师、后勤人员三层.
(2)按照的比例确定各层抽取的人数,行政人员:20×=2(人),教师:140×=14(人),后勤人员:40×=4(人).
(3)在各层中用简单随机抽样的方法抽取样本.
(4)将抽取的20人综合到一起,即得到一个样本容量为20的样本.
对比
方法
类别
共同
特点
抽样特征
相互联系
适应范围
简单随
机抽样
分层
抽样
将总体分成互不交叉的几层,按比例分层抽样
总体中的个体数较少
总体由差异明显的几部分组成
从总体中逐个不放回抽取
抽样过程中每个个体被抽取的可能性相等
各层抽样时采用简单随机抽样
1.某公司生产三种型号的轿车,产量分别为1200辆、6000辆、和2000辆.
为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车应分别抽取
、
、和
辆.
2.某所学校有小学部、初中部和高中部,在校小学生、初中生和高中生之比为5:2:3,且已知初中生有800人.现要从这所学校中抽取一个容量为80的样本以了解他们对某一问题的看法,应采用什么抽样方法?从小学部、初中部及高中部各抽取多少名?总体上看,平均多少名学生中抽取到一名学生?
当堂检测
6
30
10
1.分层抽样的概念、特征及步骤;
2.三种抽样方法相互之间的区别与联系.
课堂小结
课外阅读是开拓学生视野,发展学生智力的重要途经之一。请同学们设计份调查问卷,利用抽样的方式调查城区中小学生的阅读情况,要求按学习小组合作写出统计报告,要求体现统计数据、抽样过程和结论。
实践作业
谢谢观看
6.2.2分层随机抽样
北师大(2019)必修1
第一课时
复习回顾
简单随机抽样特点是什么?
①总体容量较小;
②逐个抽取;
③不放回抽取;
④每个个体被抽到的机会相等
情境设置
那么当总体中的个体有很大差异时,适宜采用什么抽取方法?
问题1:全国各地的人口和住户的基本情况相同吗?
不同,有很大的差异
问题2:如果用简单随机抽样或系统抽样来抽取,样本具有代表性吗?
不具有代表性
提出问题
为了估计估测高二某班全体学生(共有50人,其中男生30人,女生20人)的平均身高,我想从班级学生中抽取出容量为10的样本进行调查。
提出问题
(1)请问你将如何抽样?
(2)所抽出的样本中什么因素会对样本的平均身高产生重大影响?
(3)为什么男生,女生抽出的人数是6人和4人,而不是各抽5人呢?
数学实验
01
165
02
174
03
162
04
178
05
172
06
172
07
166
08
180
09
164
10
177
11
164
12
175
13
162
14
178
15
163
16
178
17
168
18
176
19
161
20
172
21
165
22
172
23
165
24
176
25
174
26
174
27
162
28
176
29
165
30
178
31
162
32
176
33
166
34
172
35
171
36
170
37
160
38
179
39
164
40
178
41
172
42
170
43
175
44
176
45
174
46
178
47
174
48
178
49
173
50
180
分层随机抽样
将总体按其属性特征分成互不交叉的若干类型(有时称作层),然后在每个类型中按照所占比例随机抽取一定的个体,这种抽样方法通常叫作分层随机抽样
分层随机抽样
解读
适用范围
总体“差异明显”
目
的
使样本更客观地反映总体的情况
原
则
分成“层次分明”的几部分
特
点
按各部分在总体所占的比实施抽样
分层随机抽样步骤
(1)将总体按一定的标准分层(分层)
(2)计算各层的个体数与总体的个体数的比(定比)
(3)按各层个体数与总体的个体数的比确定各层应抽取的样本容量(定量)
(4)在每一层进行抽样(抽样)
分层随机抽样思辨
判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)分层随机抽样适用于总体由差异明显的几部分组成,而层内个体间无明显差异的抽样.(
√
)
(2)在分层随机抽样中,各层抽取的个体数相等.(
×
)
(3)用分层随机抽样的方法,在分层时,每层的各个个体互不交叉,既不重复,又不遗漏.(
√
)
(4)在分层随机抽样中,每个个体被抽到的可能性是相等的,与层数及分层无关.(
√
)
?
?
?
?
分层随机抽样思辨
下列问题中,采用怎样的抽样方法较为合理?
(1)从10台冰箱中抽取3台进行质量检查;
(2)某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名.为了了解教职工对校务公开方面的意见,拟抽取一个容量为20的样本.
简单随机抽样法
分层随机抽样法
分层随机抽样应用
例1.某电视台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如表所示
很喜爱
喜爱
一般
不喜欢
2435
4567
3926
1072
电视台为进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应怎样进行抽样?
分析:人数多,差异大→分层随机抽样→确定每层抽取的比例→在各层中分别抽取→合在一起得样本
解:采用分层随机抽样的方法,抽样比为.
持“很喜爱”态度的有2
435人,应抽取2
435×≈12(人);
持“喜爱”态度的有4
567人,应抽取4
567×≈23(人);
持“一般”态度的有3
926人,应抽取3
926×≈20(人);
持“不喜爱”态度的有1
072人,应抽取1
072×≈5(人).
因此,采用分层随机抽样的方法在持“很喜爱”“喜爱”“一般”
“不喜爱”态度的人中分别抽取12人、23人、20人和5人.
解题心得
在分层随机抽样的过程中,为了保证每个个体被抽到的可能性是相等的,要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比.
分层随机抽样应用
例2.
某学校有在编人员200人,其中行政人员20人,教师140人,后勤人员40人.教育部门为了解学校职工对学校县管校聘改革的意见,要从中抽取20人,试确定用何种方法抽样,并写出抽样过程.
解:(1)将200人分成行政人员、教师、后勤人员三层.
(2)按照的比例确定各层抽取的人数,行政人员:20×=2(人),教师:140×=14(人),后勤人员:40×=4(人).
(3)在各层中用简单随机抽样的方法抽取样本.
(4)将抽取的20人综合到一起,即得到一个样本容量为20的样本.
对比
方法
类别
共同
特点
抽样特征
相互联系
适应范围
简单随
机抽样
分层
抽样
将总体分成互不交叉的几层,按比例分层抽样
总体中的个体数较少
总体由差异明显的几部分组成
从总体中逐个不放回抽取
抽样过程中每个个体被抽取的可能性相等
各层抽样时采用简单随机抽样
1.某公司生产三种型号的轿车,产量分别为1200辆、6000辆、和2000辆.
为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车应分别抽取
、
、和
辆.
2.某所学校有小学部、初中部和高中部,在校小学生、初中生和高中生之比为5:2:3,且已知初中生有800人.现要从这所学校中抽取一个容量为80的样本以了解他们对某一问题的看法,应采用什么抽样方法?从小学部、初中部及高中部各抽取多少名?总体上看,平均多少名学生中抽取到一名学生?
当堂检测
6
30
10
1.分层抽样的概念、特征及步骤;
2.三种抽样方法相互之间的区别与联系.
课堂小结
课外阅读是开拓学生视野,发展学生智力的重要途经之一。请同学们设计份调查问卷,利用抽样的方式调查城区中小学生的阅读情况,要求按学习小组合作写出统计报告,要求体现统计数据、抽样过程和结论。
实践作业
谢谢观看
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
