24.3.1锐角三角函数课件 华东师大版数学九年级上册(第一课时 27张)
文档属性
| 名称 | 24.3.1锐角三角函数课件 华东师大版数学九年级上册(第一课时 27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 838.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 12:12:35 | ||
图片预览








文档简介
(共27张PPT)
24.3锐角三角函数
第一课时
我们已经知道,直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
如图,在Rt△MNP中,∠N=90゜.
∠P的对边是_____,∠P的邻边是______;
∠M的对边是____
,∠M的邻边是______;
MN
PN
PN
MN
想一想:∠P的对边、邻边与∠M的对边、邻边有什么关系?
观察图19.3.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
B2C2
AC2
B3C3
AC3
探究
探究
A
B
C
A'
B'
C'
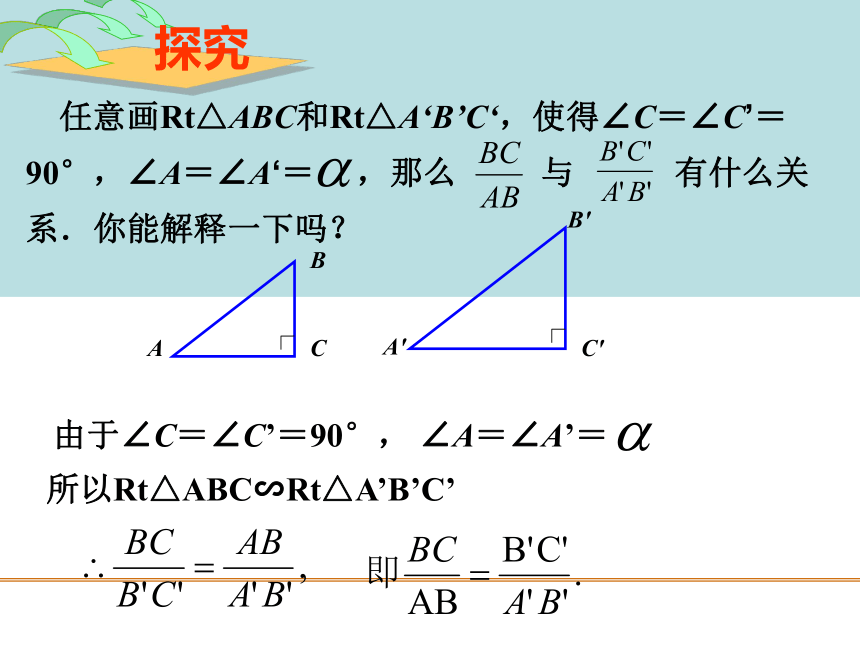
任意画Rt△ABC和Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A‘=
,那么
与
有什么关系.你能解释一下吗?
由于∠C=∠C’=90°,
∠A=∠A’=
所以Rt△ABC∽Rt△A’B’C’
这个值我们称它是∠A的三角函数值。
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个固定值.
探究
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,
即
例如,当∠A=30°时,我们有
当∠A=45°时,我们有
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
正
弦
注意:
sinA是一个完整的符号,它表示∠A的正弦,当角是用一个大写字母或度数表示时,习惯省去角的符号“∠”,如:
sin
;当用三个字母、或数字表示时,不能省略角的符号如:sin∠BAC,
sin∠1
;
sinA没有单位,它表示一个比值,即直角三角形中∠A的对边与斜边的比;
sinA不表示“sin”乘以“A”。
例1
如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
A
B
C
3
4
例
题
示
范
A
B
C
13
5
(1)
(2)
试着完成图(2)
练习
A
C
3
5
B
2、在平面直角平面坐标系中,已知点A(3,0)
和B(0,-4),则sin∠OAB等于____.
3、在Rt△ABC中,∠C=90°,AD是BC边
上的中线,AC=2,BC=4,则sin∠DAC=___.
4、在Rt△ABC中,
∠C=90°,
,
则sin∠A=___.
1、如图,求sinA和sinB的值.
想一想
对于锐角A的每一个确定的值,其邻边与斜边、对边与邻边、邻边与对边的比值也是惟一确定的
吗?
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的邻边与斜边的比叫做∠A的
余弦(cosine),记作cosA,
即
余
弦
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的对边与邻边的比叫做∠A的
正切(tangent),记作tanA,
即
正
切
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的邻边与对边的比叫做∠A的
余切,记作cotA,
即
邻边
对边
余
切
这几个比值都是锐角∠A的函数,记作sin
A、cos
A、tan
A、cot
A,即
sin
A=
cos
A=
tan
A=
cot
A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
1、sinA
不是一个角
2、sinA不是
sin与A的乘积
3、
sinA
是一个比值
4、sinA
没有单位
锐角三角函数的取值:
你能利用直角三角形的三边关系得到
sinA与
cosA的取值范围吗?
0<sin
A<1,0<cos
A<1
A
B
C
斜边c
对边a
邻边b
sin
A=
∵直角边<斜边
<1
<1
tanA、cotA的取值范围呢?
tanA>0,cotA>0
例2
如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切、余切值.
A
B
C
2
3
求出图19.3.3所示的Rt△ABC中∠A的四个三角函数值.
15
8
变式:
如图,在Rt△ABC中,∠ACB=,CD⊥AB,交AB于D,AD=3,DC=4.求∠DCB的三角函数值。
解:
∵CD⊥AB,AD=3,DC=4
∴∠ADC=
∴∠ACD+∠CAD=
∵∠ACB=∠ACD+∠BCD=
∵∠CAD=∠DCB
∴sin∠DCB=sin∠CAD==
cos∠DCB=cos∠CAD=
tan∠DCB=tan∠CAD=
cot∠DCB=cot∠CAD=
锐角三角函数性质1:相等的角的三角函数值相等。
例3、如图,若∠C=,BC:AC=2:3,求∠A的三角函数值。
解:
∴设BC=2k,AC=3k(k>0),
∵BC:AC=2:3,
∴sinA==,
cosA==,
tanA=,
cotA=
此例题中,三条边并没有具体的长度,只有两边的比值。将比例转化为具体的量,掌握设比例系数k解题的方法,即设而不求的思想。
锐角三角函数性质2:当角度一定时,它的三角函数值也就确定了,与角所在的三角形三边的长短无关。
变式:
已知在Rt△ABC中,∠C=,sinA=∠A的其他三个函数值。
解:
∵在Rt△ABC中,∠C=,
∴sinA=
∴设BC=7k,AB=25k
根据勾股定理:
∴cosA=
tanA=
cotA=
已知某个角的一个三角函数值,利用辅助比的方法得到第三条边的值,算出其他三角函数值。
例4、如图,在△ABC中,AD是边BC上的高,BC=AD=8,sinB=,求tan∠CAD的值。
解:
∵AD是边BC上的高,
∴∠ADB=∠ADC=,
△ADB、
△ADC是直角三角形。
∵sinB=,AD=8
∴AB=10
根据勾股定理:
∴DC=8-6=2
tan∠CAD===
例4、如图,在△ABC中,AD是边BC上的高,BC=AD=8,sinB=,求tan∠CAD的值。
变式:
如图,在△ABC中,AB=15,BC=13,sinB=,求tanC的值。
∟
D
解:
过A作AD⊥BC于D,
则∠ADB=∠ADC=,
△ADB、
△ADC是直角三角形。
∵sinB=,AB=15
∴AD=12
根据勾股定理:
∴DC=13-9=4
tanC==3
当条件中已知三角函数值的角不在直角三角形中时,要构造直角三角形,一般的方法是作高。但要注意不能把已知三角函数值的角分割。
记住:求三角函数值一定要在直角三角形中。
练习:
1、如图,在Rt△ABC中,∠C=,若将各边长度都扩大为原来的2倍,则∠A的弦值为(
)。
A、扩大2倍
B、缩小2倍
C、扩大4倍
D、不变
2、Rt△ABC中,∠C=,AB=4,AC=1,则cosA的值是
(
)
A、
B、
C、
D、4
3、已知△ABC中,AC=4,BC=3,AB=5,则sinA=(
)
A、
B、
C、
D、
D
B
A
A
B
C
D
4、图中∠ACB=90°
,CD⊥AB,如果CD=5,AC=10,则sin∠ACD=
,sin
∠DCB=
。
5、△ABC中,∠A、∠B、∠C的对边分别为a,b,c
,且a:b:c=8:15:17,则sinB=
,cosB=
。
小结
sin
A=
cos
A=
tan
A=
cot
A=
正弦
余弦
正切
余切
锐角A的三角函数:
三角函数性质:
1、两个相等的锐角的三角函数相等。
2、当一个锐角的角度确定后,它的三角函数值就确定了,与所在的三角形的三边的长短无关。
0<sin
A<1,0<cos
A<1
再见
24.3锐角三角函数
第一课时
我们已经知道,直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
如图,在Rt△MNP中,∠N=90゜.
∠P的对边是_____,∠P的邻边是______;
∠M的对边是____
,∠M的邻边是______;
MN
PN
PN
MN
想一想:∠P的对边、邻边与∠M的对边、邻边有什么关系?
观察图19.3.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
B2C2
AC2
B3C3
AC3
探究
探究
A
B
C
A'
B'
C'
任意画Rt△ABC和Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A‘=
,那么
与
有什么关系.你能解释一下吗?
由于∠C=∠C’=90°,
∠A=∠A’=
所以Rt△ABC∽Rt△A’B’C’
这个值我们称它是∠A的三角函数值。
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个固定值.
探究
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,
即
例如,当∠A=30°时,我们有
当∠A=45°时,我们有
A
B
C
c
a
b
对边
斜边
在图中
∠A的对边记作a
∠B的对边记作b
∠C的对边记作c
正
弦
注意:
sinA是一个完整的符号,它表示∠A的正弦,当角是用一个大写字母或度数表示时,习惯省去角的符号“∠”,如:
sin
;当用三个字母、或数字表示时,不能省略角的符号如:sin∠BAC,
sin∠1
;
sinA没有单位,它表示一个比值,即直角三角形中∠A的对边与斜边的比;
sinA不表示“sin”乘以“A”。
例1
如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
A
B
C
3
4
例
题
示
范
A
B
C
13
5
(1)
(2)
试着完成图(2)
练习
A
C
3
5
B
2、在平面直角平面坐标系中,已知点A(3,0)
和B(0,-4),则sin∠OAB等于____.
3、在Rt△ABC中,∠C=90°,AD是BC边
上的中线,AC=2,BC=4,则sin∠DAC=___.
4、在Rt△ABC中,
∠C=90°,
,
则sin∠A=___.
1、如图,求sinA和sinB的值.
想一想
对于锐角A的每一个确定的值,其邻边与斜边、对边与邻边、邻边与对边的比值也是惟一确定的
吗?
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的邻边与斜边的比叫做∠A的
余弦(cosine),记作cosA,
即
余
弦
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的对边与邻边的比叫做∠A的
正切(tangent),记作tanA,
即
正
切
如图,在Rt△ABC中,∠C=90°,
A
B
C
斜边c
对边a
邻边b
★我们把锐角A的邻边与对边的比叫做∠A的
余切,记作cotA,
即
邻边
对边
余
切
这几个比值都是锐角∠A的函数,记作sin
A、cos
A、tan
A、cot
A,即
sin
A=
cos
A=
tan
A=
cot
A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
1、sinA
不是一个角
2、sinA不是
sin与A的乘积
3、
sinA
是一个比值
4、sinA
没有单位
锐角三角函数的取值:
你能利用直角三角形的三边关系得到
sinA与
cosA的取值范围吗?
0<sin
A<1,0<cos
A<1
A
B
C
斜边c
对边a
邻边b
sin
A=
∵直角边<斜边
<1
<1
tanA、cotA的取值范围呢?
tanA>0,cotA>0
例2
如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切、余切值.
A
B
C
2
3
求出图19.3.3所示的Rt△ABC中∠A的四个三角函数值.
15
8
变式:
如图,在Rt△ABC中,∠ACB=,CD⊥AB,交AB于D,AD=3,DC=4.求∠DCB的三角函数值。
解:
∵CD⊥AB,AD=3,DC=4
∴∠ADC=
∴∠ACD+∠CAD=
∵∠ACB=∠ACD+∠BCD=
∵∠CAD=∠DCB
∴sin∠DCB=sin∠CAD==
cos∠DCB=cos∠CAD=
tan∠DCB=tan∠CAD=
cot∠DCB=cot∠CAD=
锐角三角函数性质1:相等的角的三角函数值相等。
例3、如图,若∠C=,BC:AC=2:3,求∠A的三角函数值。
解:
∴设BC=2k,AC=3k(k>0),
∵BC:AC=2:3,
∴sinA==,
cosA==,
tanA=,
cotA=
此例题中,三条边并没有具体的长度,只有两边的比值。将比例转化为具体的量,掌握设比例系数k解题的方法,即设而不求的思想。
锐角三角函数性质2:当角度一定时,它的三角函数值也就确定了,与角所在的三角形三边的长短无关。
变式:
已知在Rt△ABC中,∠C=,sinA=∠A的其他三个函数值。
解:
∵在Rt△ABC中,∠C=,
∴sinA=
∴设BC=7k,AB=25k
根据勾股定理:
∴cosA=
tanA=
cotA=
已知某个角的一个三角函数值,利用辅助比的方法得到第三条边的值,算出其他三角函数值。
例4、如图,在△ABC中,AD是边BC上的高,BC=AD=8,sinB=,求tan∠CAD的值。
解:
∵AD是边BC上的高,
∴∠ADB=∠ADC=,
△ADB、
△ADC是直角三角形。
∵sinB=,AD=8
∴AB=10
根据勾股定理:
∴DC=8-6=2
tan∠CAD===
例4、如图,在△ABC中,AD是边BC上的高,BC=AD=8,sinB=,求tan∠CAD的值。
变式:
如图,在△ABC中,AB=15,BC=13,sinB=,求tanC的值。
∟
D
解:
过A作AD⊥BC于D,
则∠ADB=∠ADC=,
△ADB、
△ADC是直角三角形。
∵sinB=,AB=15
∴AD=12
根据勾股定理:
∴DC=13-9=4
tanC==3
当条件中已知三角函数值的角不在直角三角形中时,要构造直角三角形,一般的方法是作高。但要注意不能把已知三角函数值的角分割。
记住:求三角函数值一定要在直角三角形中。
练习:
1、如图,在Rt△ABC中,∠C=,若将各边长度都扩大为原来的2倍,则∠A的弦值为(
)。
A、扩大2倍
B、缩小2倍
C、扩大4倍
D、不变
2、Rt△ABC中,∠C=,AB=4,AC=1,则cosA的值是
(
)
A、
B、
C、
D、4
3、已知△ABC中,AC=4,BC=3,AB=5,则sinA=(
)
A、
B、
C、
D、
D
B
A
A
B
C
D
4、图中∠ACB=90°
,CD⊥AB,如果CD=5,AC=10,则sin∠ACD=
,sin
∠DCB=
。
5、△ABC中,∠A、∠B、∠C的对边分别为a,b,c
,且a:b:c=8:15:17,则sinB=
,cosB=
。
小结
sin
A=
cos
A=
tan
A=
cot
A=
正弦
余弦
正切
余切
锐角A的三角函数:
三角函数性质:
1、两个相等的锐角的三角函数相等。
2、当一个锐角的角度确定后,它的三角函数值就确定了,与所在的三角形的三边的长短无关。
0<sin
A<1,0<cos
A<1
再见
