5.3.3三角函数的诱导公式-【新教材】2020-2021学年人教A版(2019)高中数学必修第一册导学案
文档属性
| 名称 | 5.3.3三角函数的诱导公式-【新教材】2020-2021学年人教A版(2019)高中数学必修第一册导学案 | 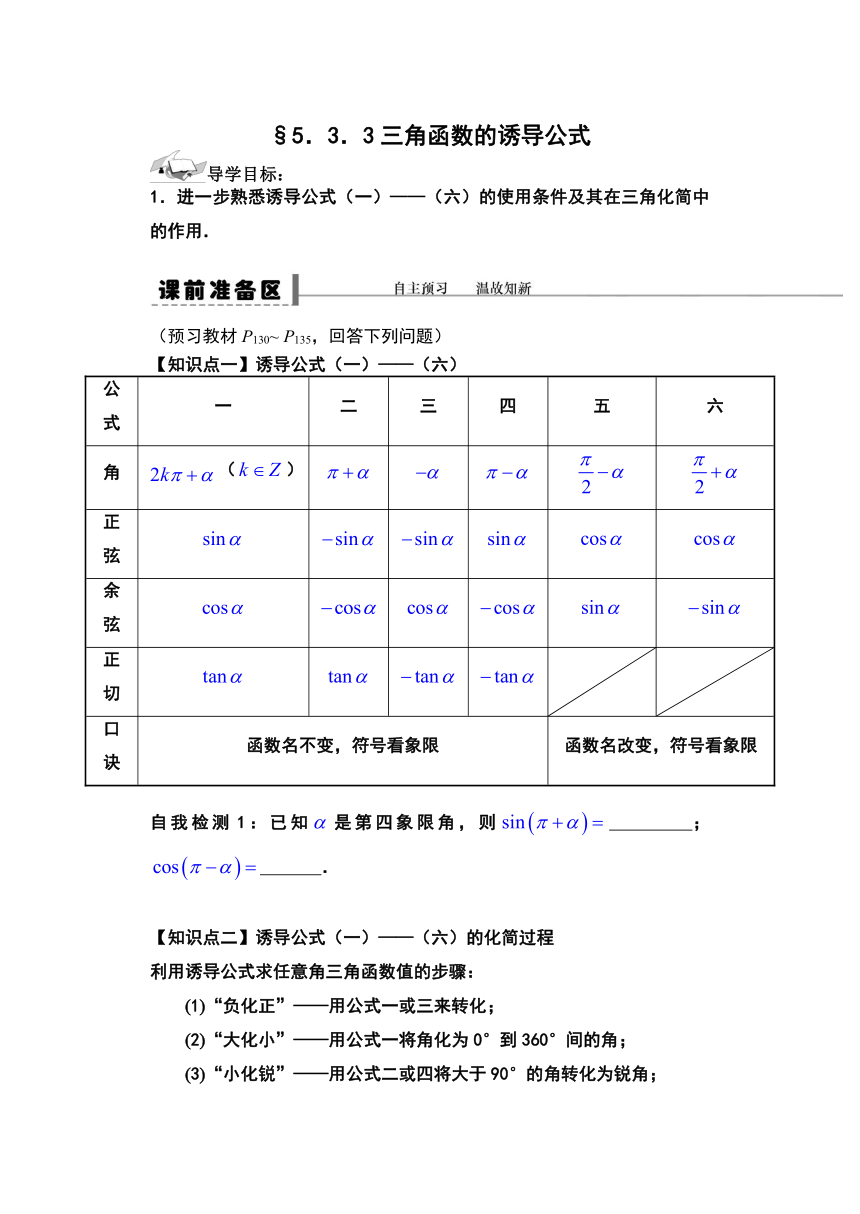 | |
| 格式 | doc | ||
| 文件大小 | 864.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 19:19:36 | ||
图片预览





文档简介
§5.3.3三角函数的诱导公式
导学目标:
1.进一步熟悉诱导公式(一)——(六)的使用条件及其在三角化简中的作用.
(预习教材P130~
P135,回答下列问题)
【知识点一】诱导公式(一)——(六)
公式
一
二
三
四
五
六
角
()
正弦
余弦
正切
口诀
函数名不变,符号看象限
函数名改变,符号看象限
自我检测1:已知是第四象限角,则
;
.
【知识点二】诱导公式(一)——(六)的化简过程
利用诱导公式求任意角三角函数值的步骤:
1“负化正”——用公式一或三来转化;
2“大化小”——用公式一将角化为0°到360°间的角;
3“小化锐”——用公式二或四将大于90°的角转化为锐角;
4“锐求值”——得到锐角的三角函数后求值.
诱导公式的基本流程如下图:
注意:解题时应多观察所涉及的角之间的关系,如果两者之差或和为的整数倍,
可考虑使用诱导公式进行化简,如:
;;.
自我检测2:(1)已知,那么
.
(2)若,那么
.
题型一
诱导公式(一)——(六)的正确使用
【例1-1】已知,求的值.
【例1-2】已知.
(1)化简;
(2)若,且为第二象限角,求的值;
(3)若,求的值.
题型二
诱导公式在三角形中的应用
【例2】在中常用到以下结论:
(1)
;
;
.
;
.
(2)若为锐角三角形,则有
()
(3)在中,,且,则等于( )
A.
B.
C.
D.
题型三
角的变换——诱导形式
【例3-1】已知,则________.
【例3-2】若,则________.
1.计算:
( )
A.
B.
C.
D.
2.已知,,则
( )
A.
B.
C.
D.
3.设为锐角,若,则的值为(
)
A.
B.
C.
D.
4.已知为锐角,且,,,则的值是(
)
A.
B.
C.
D.
5.
在中,
,且,则等于
.
§5.3.3三角函数的诱导公式答案
导学目标:
1.进一步熟悉诱导公式(一)——(六)的使用条件及其在三角化简中的作用.
(预习教材P130~
P135,回答下列问题)
【知识点一】诱导公式(一)——(六)
公式
一
二
三
四
五
六
角
()
正弦
余弦
正切
口诀
函数名不变,符号看象限
函数名改变,符号看象限
自我检测1:已知是第四象限角,则
;
.
【知识点二】诱导公式(一)——(六)的化简过程
利用诱导公式求任意角三角函数值的步骤:
1“负化正”——用公式一或三来转化;
2“大化小”——用公式一将角化为0°到360°间的角;
3“小化锐”——用公式二或四将大于90°的角转化为锐角;
4“锐求值”——得到锐角的三角函数后求值.
诱导公式的基本流程如下图:
注意:解题时应多观察所涉及的角之间的关系,如果两者之差或和为的整数倍,
可考虑使用诱导公式进行化简,如:
;;.
自我检测2:(1)已知,那么
.
(2)若,那么
.
【答案】(1)(2)
题型一
诱导公式(一)——(六)的正确使用
【例1-1】已知,求的值.
【答案】由,得,即,
∴.
【例1-2】已知.
(1)化简;
(2)若,且为第二象限角,求的值;
(3)若,求的值.
【答案】(1)原式
(2)
(3)由,即,所以.
.
?
题型二
诱导公式在三角形中的应用
【例2】在中常用到以下结论:
(1)
;
;
.
;
.
(2)若为锐角三角形,则有
()
(3)在中,,且,则等于( )
A.
B.
C.
D.
【答案】C
因为sin=3sin(π-A),所以cosA=3sinA,所以tanA=,又0题型三
角的变换——诱导形式
【例3-1】已知,则________.
【答案】cos(α+)=cos[(α+)+]=-sin(α+)=-.
【例3-2】若,则________.
【答案】因为cos=cos=-cos=-a.
sin=sin=cos=a,
所以cos+sin=0.
1.计算:
( )
A.
B.
C.
D.
【答案】A
2.已知,,则
( )
A.
B.
C.
D.
【答案】C
3.设为锐角,若,则的值为(
)
A.
B.
C.
D.
4.已知为锐角,且,,,则的值是(
)
A.
B.
C.
D.
【答案】B
5.
在中,
,且,则等于
.
【答案】
导学目标:
1.进一步熟悉诱导公式(一)——(六)的使用条件及其在三角化简中的作用.
(预习教材P130~
P135,回答下列问题)
【知识点一】诱导公式(一)——(六)
公式
一
二
三
四
五
六
角
()
正弦
余弦
正切
口诀
函数名不变,符号看象限
函数名改变,符号看象限
自我检测1:已知是第四象限角,则
;
.
【知识点二】诱导公式(一)——(六)的化简过程
利用诱导公式求任意角三角函数值的步骤:
1“负化正”——用公式一或三来转化;
2“大化小”——用公式一将角化为0°到360°间的角;
3“小化锐”——用公式二或四将大于90°的角转化为锐角;
4“锐求值”——得到锐角的三角函数后求值.
诱导公式的基本流程如下图:
注意:解题时应多观察所涉及的角之间的关系,如果两者之差或和为的整数倍,
可考虑使用诱导公式进行化简,如:
;;.
自我检测2:(1)已知,那么
.
(2)若,那么
.
题型一
诱导公式(一)——(六)的正确使用
【例1-1】已知,求的值.
【例1-2】已知.
(1)化简;
(2)若,且为第二象限角,求的值;
(3)若,求的值.
题型二
诱导公式在三角形中的应用
【例2】在中常用到以下结论:
(1)
;
;
.
;
.
(2)若为锐角三角形,则有
()
(3)在中,,且,则等于( )
A.
B.
C.
D.
题型三
角的变换——诱导形式
【例3-1】已知,则________.
【例3-2】若,则________.
1.计算:
( )
A.
B.
C.
D.
2.已知,,则
( )
A.
B.
C.
D.
3.设为锐角,若,则的值为(
)
A.
B.
C.
D.
4.已知为锐角,且,,,则的值是(
)
A.
B.
C.
D.
5.
在中,
,且,则等于
.
§5.3.3三角函数的诱导公式答案
导学目标:
1.进一步熟悉诱导公式(一)——(六)的使用条件及其在三角化简中的作用.
(预习教材P130~
P135,回答下列问题)
【知识点一】诱导公式(一)——(六)
公式
一
二
三
四
五
六
角
()
正弦
余弦
正切
口诀
函数名不变,符号看象限
函数名改变,符号看象限
自我检测1:已知是第四象限角,则
;
.
【知识点二】诱导公式(一)——(六)的化简过程
利用诱导公式求任意角三角函数值的步骤:
1“负化正”——用公式一或三来转化;
2“大化小”——用公式一将角化为0°到360°间的角;
3“小化锐”——用公式二或四将大于90°的角转化为锐角;
4“锐求值”——得到锐角的三角函数后求值.
诱导公式的基本流程如下图:
注意:解题时应多观察所涉及的角之间的关系,如果两者之差或和为的整数倍,
可考虑使用诱导公式进行化简,如:
;;.
自我检测2:(1)已知,那么
.
(2)若,那么
.
【答案】(1)(2)
题型一
诱导公式(一)——(六)的正确使用
【例1-1】已知,求的值.
【答案】由,得,即,
∴.
【例1-2】已知.
(1)化简;
(2)若,且为第二象限角,求的值;
(3)若,求的值.
【答案】(1)原式
(2)
(3)由,即,所以.
.
?
题型二
诱导公式在三角形中的应用
【例2】在中常用到以下结论:
(1)
;
;
.
;
.
(2)若为锐角三角形,则有
()
(3)在中,,且,则等于( )
A.
B.
C.
D.
【答案】C
因为sin=3sin(π-A),所以cosA=3sinA,所以tanA=,又0
角的变换——诱导形式
【例3-1】已知,则________.
【答案】cos(α+)=cos[(α+)+]=-sin(α+)=-.
【例3-2】若,则________.
【答案】因为cos=cos=-cos=-a.
sin=sin=cos=a,
所以cos+sin=0.
1.计算:
( )
A.
B.
C.
D.
【答案】A
2.已知,,则
( )
A.
B.
C.
D.
【答案】C
3.设为锐角,若,则的值为(
)
A.
B.
C.
D.
4.已知为锐角,且,,,则的值是(
)
A.
B.
C.
D.
【答案】B
5.
在中,
,且,则等于
.
【答案】
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
