1.2函数及其表示复习课学案-2021-2022学年高一上学期数学人教A版必修一
文档属性
| 名称 | 1.2函数及其表示复习课学案-2021-2022学年高一上学期数学人教A版必修一 |

|
|
| 格式 | docx | ||
| 文件大小 | 507.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 19:26:17 | ||
图片预览




文档简介
函数的表示复习课
一.函数的表示法
二.分段函数
在函数定义域内,对于自变量x的不同取值范围,函数有着不同的_________.
考题一
待定系数法求函数解析式
1.已知f(x)是一次函数,f(f(f(x)))=8x+7,求f(x)的解析式.
2.已知f(x)是二次函数,且f(0)=0,f(x+1)=f(x)+x+1,则f(x)=________.
3.已知f(x)是一次函数,2f(2)?3f(1)=5,2f(0)?f(?1)=1,则f(x)=______.
考题二
换元法求函数解析式
1.已知f()=x+2,求f(x)的解析式.
2.已知,求f(x)的解析式.
3.已知函数若则函数g(x)的解析式为(
)
A.
B.
C.
D.
4.若函数f(x)=2x?3,且f(2a?1)=6,则a等于________.
5.已知f(2x+1)=4x2,则f(?3)=(
)
A.?36
B.?16
C.?4
D.??16
考题三
配凑法求函数解析式
1.已知
2.已知f()=,求f(x)
考题四
方程组法求函数解析式
1.已知
2.定义域为R的函数f(x)满足f(x)-2f(-x)=2x+1,求f(x).
3.设函数f(x)对x≠0的一切实数均有,则f(2018)等于______.
考题五
分段函数求值
1.已知函数求(1)的值;(2)若f(a)=3,求实数a的值;(3)若f(m)<0,求.m的取值范围。
2.已知,求f(7)的值.
3.设函数,若f(f(a))?3,则实数a的取值范围是___.
考题六
分段函数图像
1.画出函数y=的图象。
2.已知函数f(x)=1+(-2(1)用分段函数的形式表示该函数.(2)画出该函数的图象.(3)写出该函数的值域.
3.画出下列函数图象。
(1)y=|x2-2x-3|
(2)y=x2+2|x|-3
4.函数f(x)=[x]的函数值表示不超过x的最大整数,当时,下列函数中,其值域与f(x)的值域不相同的函数为(
)
A.?y=x,x∈{?1,0,1,2,3}
B.?y=2x,x∈
C.?,x∈
D.?,x∈
5.如图,平面图形中阴影部分面积S是h(h∈[0,H])的函数,则该函数的图象大致是()
6.已知函数,若f(a)=3,则a的值为______.
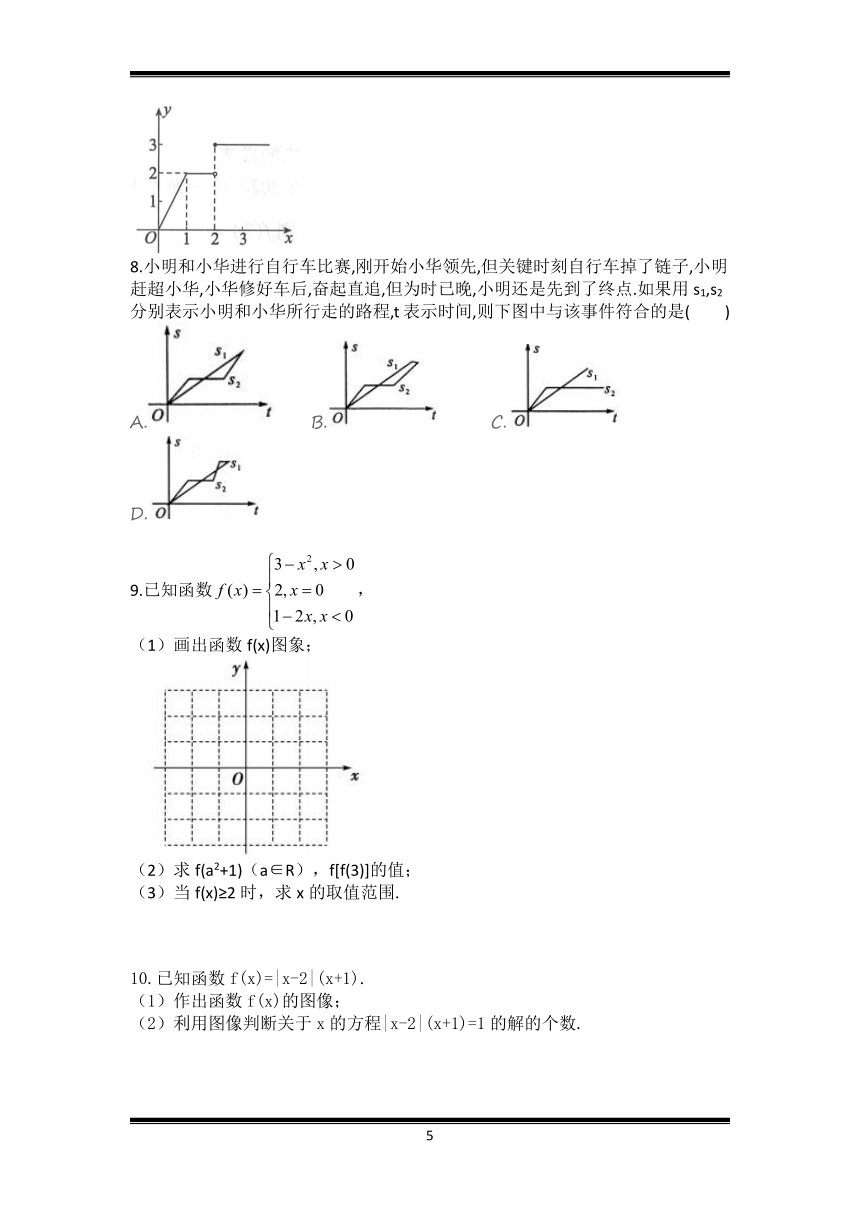
7.已知函数f(x)的图像如图,试写出一个可能的解析式为______.
8.小明和小华进行自行车比赛,刚开始小华领先,但关键时刻自行车掉了链子,小明赶超小华,小华修好车后,奋起直追,但为时已晚,小明还是先到了终点.如果用s1,s2分别表示小明和小华所行走的路程,t表示时间,则下图中与该事件符合的是( )
A.
B.
C.
D.?
9.已知函数,
(1)画出函数f(x)图象;
(2)求f(a2+1)(a∈R),f[f(3)]的值;
(3)当f(x)≥2时,求x的取值范围.
10.已知函数f(x)=|x-2|(x+1).
(1)作出函数f(x)的图像;
(2)利用图像判断关于x的方程|x-2|(x+1)=1的解的个数.
11.已知二次函数,满足,且不等式的解集为(1,2).
(1)求函数f(x)的解析式;
(2)若方程f(x)=x+d在(0,4]上有解,求实数d的取值范围.
扩展训练
已知f(x)=x2+2x+a,f(bx)=9x2-6x+2,则方程f(ax+b)=0的解集为___________.
2.函数y=f(x)的图象如图所示,则函数y=f(x)的解析式为 ( )
A.f(x)=(x-a)2(b-x)
B.f(x)=(x-a)2(x+b)
C.f(x)=-(x-a)2(x+b)
D.f(x)=(x-a)2(x-b)
3.设f(x)是R上的函数,且满足f(0)=1,并且对任意的实数x,y,有f(x-y)=f(x)-y(2x-y+1),求f(x)的解析式.
4.已知函数f(x)=若f(f(x))=2,则x的取值范围是 ( )
A.?
B.[-1,1]
C.(-∞,-1)∪(1,+∞)
D.{2}∪[-1,1]
5.设集合A=,B=,函数f(x)=若x0∈A,且f(f(x0))∈A,则x0的取值范围是 .
6.已知函数f(x)=,求不等式x+(x+1)f(x+1)≤3的解集。
7.已知函数,若f(-a)+f(a)≤0,则实数a的取值范围是(
)
A.[-1,1]
B.[-2,0]
C.[0,2]
D.[-2,2]
8.若方程x2-4|x|+3=m有4个互不相等的实数根,求m的取值范围。
9.定义运算ab=,设f(x)=(x2-1)(x-x2),若函数y=f(x)-c的图像与x轴恰有两三个公共点,求实数c的取值范围。
10.设函数g(x)=x2-2,f(x)=,求f(x)的值域。
11.某城市出租车起步价为10元,最长可租乘3km(含3km),以后每1km为1.6元(不足1km,按1km计费),若出租车行驶在不需等待的公路上,则出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为 ( )
12.已知函数f(x)满足f(x)+2f(3-x)=x2,则f(x)的解析式为 ( )
A.f(x)=x2-12x+18
B.f(x)=x2-4x+6
C.f(x)=6x+9
D.f(x)=2x+3
13.高为H、满缸水量为V的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象是 ( )
14.已知函数,若c=0,则f(x)的值域是___;若f(x)的值域是,则实数c的取值范围是___.
1
|初一·数学·基础-提高-精英·学生版|
第1讲
第页
一.函数的表示法
二.分段函数
在函数定义域内,对于自变量x的不同取值范围,函数有着不同的_________.
考题一
待定系数法求函数解析式
1.已知f(x)是一次函数,f(f(f(x)))=8x+7,求f(x)的解析式.
2.已知f(x)是二次函数,且f(0)=0,f(x+1)=f(x)+x+1,则f(x)=________.
3.已知f(x)是一次函数,2f(2)?3f(1)=5,2f(0)?f(?1)=1,则f(x)=______.
考题二
换元法求函数解析式
1.已知f()=x+2,求f(x)的解析式.
2.已知,求f(x)的解析式.
3.已知函数若则函数g(x)的解析式为(
)
A.
B.
C.
D.
4.若函数f(x)=2x?3,且f(2a?1)=6,则a等于________.
5.已知f(2x+1)=4x2,则f(?3)=(
)
A.?36
B.?16
C.?4
D.??16
考题三
配凑法求函数解析式
1.已知
2.已知f()=,求f(x)
考题四
方程组法求函数解析式
1.已知
2.定义域为R的函数f(x)满足f(x)-2f(-x)=2x+1,求f(x).
3.设函数f(x)对x≠0的一切实数均有,则f(2018)等于______.
考题五
分段函数求值
1.已知函数求(1)的值;(2)若f(a)=3,求实数a的值;(3)若f(m)<0,求.m的取值范围。
2.已知,求f(7)的值.
3.设函数,若f(f(a))?3,则实数a的取值范围是___.
考题六
分段函数图像
1.画出函数y=的图象。
2.已知函数f(x)=1+(-2
3.画出下列函数图象。
(1)y=|x2-2x-3|
(2)y=x2+2|x|-3
4.函数f(x)=[x]的函数值表示不超过x的最大整数,当时,下列函数中,其值域与f(x)的值域不相同的函数为(
)
A.?y=x,x∈{?1,0,1,2,3}
B.?y=2x,x∈
C.?,x∈
D.?,x∈
5.如图,平面图形中阴影部分面积S是h(h∈[0,H])的函数,则该函数的图象大致是()
6.已知函数,若f(a)=3,则a的值为______.
7.已知函数f(x)的图像如图,试写出一个可能的解析式为______.
8.小明和小华进行自行车比赛,刚开始小华领先,但关键时刻自行车掉了链子,小明赶超小华,小华修好车后,奋起直追,但为时已晚,小明还是先到了终点.如果用s1,s2分别表示小明和小华所行走的路程,t表示时间,则下图中与该事件符合的是( )
A.
B.
C.
D.?
9.已知函数,
(1)画出函数f(x)图象;
(2)求f(a2+1)(a∈R),f[f(3)]的值;
(3)当f(x)≥2时,求x的取值范围.
10.已知函数f(x)=|x-2|(x+1).
(1)作出函数f(x)的图像;
(2)利用图像判断关于x的方程|x-2|(x+1)=1的解的个数.
11.已知二次函数,满足,且不等式的解集为(1,2).
(1)求函数f(x)的解析式;
(2)若方程f(x)=x+d在(0,4]上有解,求实数d的取值范围.
扩展训练
已知f(x)=x2+2x+a,f(bx)=9x2-6x+2,则方程f(ax+b)=0的解集为___________.
2.函数y=f(x)的图象如图所示,则函数y=f(x)的解析式为 ( )
A.f(x)=(x-a)2(b-x)
B.f(x)=(x-a)2(x+b)
C.f(x)=-(x-a)2(x+b)
D.f(x)=(x-a)2(x-b)
3.设f(x)是R上的函数,且满足f(0)=1,并且对任意的实数x,y,有f(x-y)=f(x)-y(2x-y+1),求f(x)的解析式.
4.已知函数f(x)=若f(f(x))=2,则x的取值范围是 ( )
A.?
B.[-1,1]
C.(-∞,-1)∪(1,+∞)
D.{2}∪[-1,1]
5.设集合A=,B=,函数f(x)=若x0∈A,且f(f(x0))∈A,则x0的取值范围是 .
6.已知函数f(x)=,求不等式x+(x+1)f(x+1)≤3的解集。
7.已知函数,若f(-a)+f(a)≤0,则实数a的取值范围是(
)
A.[-1,1]
B.[-2,0]
C.[0,2]
D.[-2,2]
8.若方程x2-4|x|+3=m有4个互不相等的实数根,求m的取值范围。
9.定义运算ab=,设f(x)=(x2-1)(x-x2),若函数y=f(x)-c的图像与x轴恰有两三个公共点,求实数c的取值范围。
10.设函数g(x)=x2-2,f(x)=,求f(x)的值域。
11.某城市出租车起步价为10元,最长可租乘3km(含3km),以后每1km为1.6元(不足1km,按1km计费),若出租车行驶在不需等待的公路上,则出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为 ( )
12.已知函数f(x)满足f(x)+2f(3-x)=x2,则f(x)的解析式为 ( )
A.f(x)=x2-12x+18
B.f(x)=x2-4x+6
C.f(x)=6x+9
D.f(x)=2x+3
13.高为H、满缸水量为V的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为v,则函数v=f(h)的大致图象是 ( )
14.已知函数,若c=0,则f(x)的值域是___;若f(x)的值域是,则实数c的取值范围是___.
1
|初一·数学·基础-提高-精英·学生版|
第1讲
第页
