9.2库仑定律 课件(26张PPT)
文档属性
| 名称 | 9.2库仑定律 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-04 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第九章 静电场及其应用
9.2
库仑定律
目录
知识讲解
小结
练习
上节回溯
电荷
两种电荷:正电荷和负电荷
特性:同性相吸,异性相斥
三种使物体带电的方法
电荷量:定义;单位;
上节回溯
方法:摩擦起电、接触起电、感应起电
现象:
实质:均是电子发生转移
电荷守恒定律
表述一:
表述二:
定义:一个电子的电荷量
大小:e=1.602176634×10-19
C
比荷:电子的电荷量与电子质量之比
电子的质量:me=9.11×10-31
kg
元电荷
上节回溯
一、电荷之间的作用力
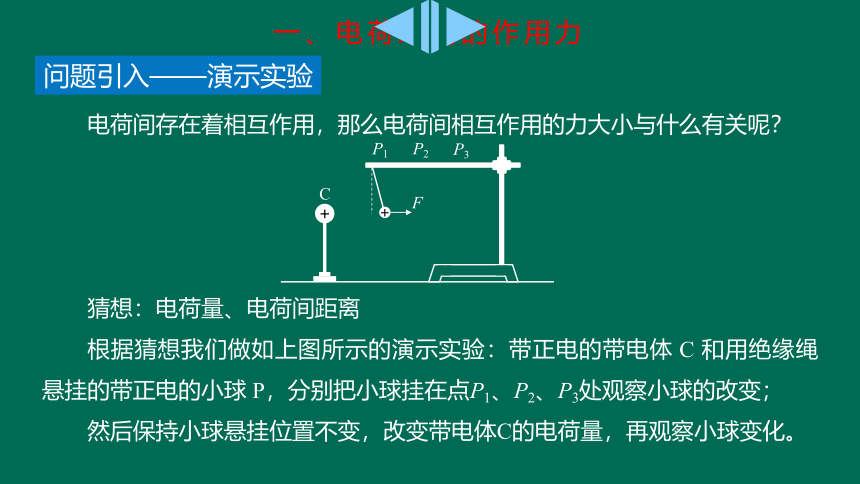
问题引入——演示实验
+
+
F
P1
P2
P3
C
电荷间存在着相互作用,那么电荷间相互作用的力大小与什么有关呢?
猜想:电荷量、电荷间距离
根据猜想我们做如上图所示的演示实验:带正电的带电体
C
和用绝缘绳悬挂的带正电的小球
P,分别把小球挂在点P1、P2、P3处观察小球的改变;
然后保持小球悬挂位置不变,改变带电体C的电荷量,再观察小球变化。
一、电荷之间的作用力
库仑定律
库仑(1736-1806)
类比万有引力定律,在库仑定律建立的过程中发挥了重要作用,英国科学家卡文迪什和普利斯特等人确信“平方反比”规律适用于电荷间的力。最终,库仑通过自己设计的扭秤实验解决了这一问题,建立了库仑定律。
通过刚刚的演示实验,我们可以看到,电荷之间的作用力随着电荷量的增大而增大,随着距离的增大而减小。
电荷间的作用规律跟万有引力定律是不是有些相似?
一、电荷之间的作用力
库仑定律
1.内容:真空中两个静止的点电荷之间的相互作用力,与它们电荷量的乘积
成正比,与它们的距离的二次方成反比,作用力的方向在它们的连
线上。
2.条件:真空中两个静止的点电荷。
3.静电力:电荷之间的相互作用力,又叫作库仑力。
一、电荷之间的作用力
点电荷
1.定义:当带电体之间的距离比它们自身的大小大得多,以致带电体的形状、大小及电荷分布状况对它们之间的作用力的影响可以忽略时,这样的带电体可以看做带电的点,这样的点,叫作点电荷。
2.是为了简化一些问题而建立的理想化物理模型
3.点电荷本身的大小可以很大,电荷量也可以很大,这一点的概念“类似”力学中的质点的概念。
一、电荷之间的作用力
点电荷
例1 下列关于点电荷的说法中正确的是 (
)
体积大的带电体一定不能看成点电荷
当两个带电体的大小、形状以及电荷分布情况对它们间相互作用力的影响可以忽略时,这两个带电体可以看成点电荷
点电荷就是体积足够小的电荷
点电荷就是体积和电荷量都很小的带电体
B
二、库仑的实验
库仑扭秤实验
1.改变
A
和
C
之间的距离
r,记录每次悬丝扭转的角度,就可以找到力
F
与距离
r
的关系:
2.库仑那个年代无法测量电荷量,就利用两个相同的金属小球,一个带电,一个不带电,接触后各带一半的电荷量,多次重复,可以把小球的电荷量分为:、、……
最终得出力与电荷量之间的关系:
F
q1q2
带电小球
C
带电小球
A
不带电
平衡小球
B
细银丝
二、库仑的实验
库仑定律的公式
1.公式:
2.比例系数:k=9.0×109
N·m2/C2
这个比例系数叫作静电力常量
3.方向:在两个点电荷的连线上,同种电荷,它们之间的作用力叫作斥力,异种电荷之间的作用力叫作引力。
+
q1
q2
r
F
1
F
2
F
1
+
+
q1
r
F
2
q2
三、静电力的计算
静电力
根据库仑定律得到公式:
比例系数:k=9.0×109
N·m2/C2
这个比例系数叫作静电力常量
根据库仑定律,两个
1C
的点电荷在真空中相距
1m
时,相互作用力是
9.0×109N
,差不多相当于一百多万吨的物体所受的重力,可见库仑是一个非常大的单位。
通常一把梳子和衣服摩擦后所带的电荷量不到百万分之一库仑,闪电产生前,云层积累的电荷量可达几百库仑。
三、静电力的计算
静电力与万有引力
静电力
万有引力
公式
比例系数
静电力常量:
k=9.0×109
N·m2/C2
万有引力常量:
G=6.67×10-11
N·m2/kg2
作用方向
作用力方向在它们的连线上
作用关系
两个点电荷之间的相互作用,可以是引力,也可以是斥力
任意两个物体之间的相互作用,只为引力
相同点
均是与描述的相互作用有关的物理量的乘积成正比;与距离的平方成反比;作用力的方向均在两物体的连线上
三、静电力的计算
静电力与万有引力
例1 在氢原子内,氢原子核与电子之间的最短距离为5.3×10-11m
。试比较氢原子与电子之间的静电力与万有引力。
分析 氢原子核与质子所带的电荷量相同,是1.6×10-19C
。电子带负电,所带的电荷量也是1.6×10-19C
。质子质量为1.6×10-27
kg,电子质量为9.1×10-31
kg
。根据库仑定律和万有引力定律就可以求解。
解 根据库仑定律,它们之间的静电力:
=9.0×109×
N=8.2×10-8
N
三、静电力的计算
静电力与万有引力
根据万有引力定律,它们之间的万有引力
=6.7×10-11×
N=3.6×10-47
N
=2.3×1039
氢原子核与电子之间的静电力是万有引力的
2.3×1039
倍
可见,微观粒子间的万有引力远小于库仑力。因此研究微观粒子的相互作用时,可以忽略万有引力。
三、静电力的计算
多个点电荷间的静电力
库仑定律描述的是两个点电荷之间的相互作用力。如果存在两个以上点电荷,那么,每个点电荷都要受到其他所有点电荷对它的作用力。两个或两个以上点电荷对某一点电荷的作用力,等于各个点电荷单独对这个点电荷的作用力的矢量和。
真空中两个静止的点电荷间的相互作用力的大小只跟两个点电荷的电荷量和间距有关,跟它们的周围是否存在其他点电荷无关。
三、静电力的计算
多个点电荷间的静电力
例2 真空中有三个带正电的点电荷,它们固定在边长为
50cm
的等边三角形的三个顶点上,每个点电荷的电荷量都是
2.0×10-6
C
,求它们各自所受的静电力。
+
+
+
q1
q2
q3
F1
F2
F
分析 根据题目意思作图。每个点电荷都受到其他两个点电荷的斥力,因此,只要求出一个点电荷(例如q3)所受的力即可。
解 根据库仑定律,点电荷
q3
共受到
F1
和
F2
两个力的作用,其中
q1=q2=q3=q
三、静电力的计算
多个点电荷间的静电力
每两个点电荷之间的距离
r
都相同,所以
F1=F2=k
=
N=0.144
N
根据平行四边形定则可得
F=2F1
cos
30°=0.25
N
点电荷
q3
所受的合力
F
的方向为
q1
和
q2
连线的垂直平分线向外。
每个点电荷所受的静电力大小相等,数值均为
0.25
N
,方向均沿另外两个点电荷连线的垂直平分线向外。
库仑定律
静电力:电荷间的相互作用力,又叫库仑力
库仑定律的适用条件:真空两个静止的点电荷间的相互作用力
小结
大小:与它们的电荷量的乘积成正比;与它们距离的平方成反比
方向:在它们的连线上,同性相斥,异性相吸
点电荷:带电体之间的距离远大于它们自身的大小
带电体的大小、形状及电荷分布状况对它们的影响可
以忽略
静电力的计算
公式:
k=9.0×109
N·m2/C2
这个比例系数叫作静电力常量
适用条件:真空两个静止的点电荷
小结
方向:在它们的连线上,同性相斥,异性相吸
两个点电荷间的作用力不会因为第三个点电荷的存在而改变
两个或两个以上点电荷对某一个点电荷的作用力等于各个点电荷单独对这个点电荷的作用力的矢量和
1.下列关于点电荷的说法正确的是
(
)
电荷量很小的带电体就是点电荷
一个电子,不论在任何情况下,都可以看成点电荷
当两个带电体的大小远小于它们之间的距离时,可以将这两个带电体看成点电荷
一切带电体都可以看成点电荷
练习
C
2.有三个完全相同的金属球,球
A
带的电荷量为
q,球
B
和球
C
均不带电。现在要使球
B
带的电荷量为
,应该怎么操作?
练习
答:根据库仑的发现,两个相同的带电金属球接触后所带的电荷量相等。所以,先把球
A
和球
B
接触后分开,此时球
B
带电
q/2;再把球
B
和球
C
接触后分开,则球
B、球
C
分别带电
q/4;最后,球
B
再次与球
A
接触后分开,球
B
带电
qB=
3.半径为
r
的两个金属球,其球心相距
3r,现使两球带上等量的同种电荷
Q,两球之间的静电力
F=k
吗?请说明理由。
练习
答:不等于。因为库仑定律的适用条件是真空中的点电荷,两个半径为
r
的金属球球心相距
3r
时,由于距离太近电荷分布发生变化,两球已经不能视为点电荷,因而它们之间的作用力的大小不能直接用库仑定律进行计算,所以
F
≠
k
4.如图所示,有三个点电荷
A、B、C
位于一个等边三角形的三个顶点上,已知
A、B
都带正电荷,A
所受B、C
两个点电荷的静电力合力如图中
FA
所示,那么可以判断点电荷
C
所带电荷的电性为
(
)
一定是正电
一定是负电
可能是正电,也可能是负电
无法确定
练习
+
+
A
B
C
FA
B
5.在边长为
a
的正方形的每个顶点都放置一个电荷量为
q
的同种点电荷。如果保持它们的位置不变,每个点电荷受到其他三个点电荷的静电力的合力是多少?
练习
答:分析点电荷
q4
的受力情况如右图,q4
共受到三个力的作用,由于q1=q2=q3=q4=q,相互间的距离分别为a、a、a,所以
F1=F3=kF2=k
根据平行四边形定则,合力沿对角线的连线向外,且大小是:
F=2F1cos45°+F2=
由于对称性,每个点电荷受到其他三个电荷的静电力合力的大小都相等,且都沿对角线方向向外。
q4
F3
q1
q2
q3
a
a
a
a
F1
F2
谢谢
第九章 静电场及其应用
9.2
库仑定律
目录
知识讲解
小结
练习
上节回溯
电荷
两种电荷:正电荷和负电荷
特性:同性相吸,异性相斥
三种使物体带电的方法
电荷量:定义;单位;
上节回溯
方法:摩擦起电、接触起电、感应起电
现象:
实质:均是电子发生转移
电荷守恒定律
表述一:
表述二:
定义:一个电子的电荷量
大小:e=1.602176634×10-19
C
比荷:电子的电荷量与电子质量之比
电子的质量:me=9.11×10-31
kg
元电荷
上节回溯
一、电荷之间的作用力
问题引入——演示实验
+
+
F
P1
P2
P3
C
电荷间存在着相互作用,那么电荷间相互作用的力大小与什么有关呢?
猜想:电荷量、电荷间距离
根据猜想我们做如上图所示的演示实验:带正电的带电体
C
和用绝缘绳悬挂的带正电的小球
P,分别把小球挂在点P1、P2、P3处观察小球的改变;
然后保持小球悬挂位置不变,改变带电体C的电荷量,再观察小球变化。
一、电荷之间的作用力
库仑定律
库仑(1736-1806)
类比万有引力定律,在库仑定律建立的过程中发挥了重要作用,英国科学家卡文迪什和普利斯特等人确信“平方反比”规律适用于电荷间的力。最终,库仑通过自己设计的扭秤实验解决了这一问题,建立了库仑定律。
通过刚刚的演示实验,我们可以看到,电荷之间的作用力随着电荷量的增大而增大,随着距离的增大而减小。
电荷间的作用规律跟万有引力定律是不是有些相似?
一、电荷之间的作用力
库仑定律
1.内容:真空中两个静止的点电荷之间的相互作用力,与它们电荷量的乘积
成正比,与它们的距离的二次方成反比,作用力的方向在它们的连
线上。
2.条件:真空中两个静止的点电荷。
3.静电力:电荷之间的相互作用力,又叫作库仑力。
一、电荷之间的作用力
点电荷
1.定义:当带电体之间的距离比它们自身的大小大得多,以致带电体的形状、大小及电荷分布状况对它们之间的作用力的影响可以忽略时,这样的带电体可以看做带电的点,这样的点,叫作点电荷。
2.是为了简化一些问题而建立的理想化物理模型
3.点电荷本身的大小可以很大,电荷量也可以很大,这一点的概念“类似”力学中的质点的概念。
一、电荷之间的作用力
点电荷
例1 下列关于点电荷的说法中正确的是 (
)
体积大的带电体一定不能看成点电荷
当两个带电体的大小、形状以及电荷分布情况对它们间相互作用力的影响可以忽略时,这两个带电体可以看成点电荷
点电荷就是体积足够小的电荷
点电荷就是体积和电荷量都很小的带电体
B
二、库仑的实验
库仑扭秤实验
1.改变
A
和
C
之间的距离
r,记录每次悬丝扭转的角度,就可以找到力
F
与距离
r
的关系:
2.库仑那个年代无法测量电荷量,就利用两个相同的金属小球,一个带电,一个不带电,接触后各带一半的电荷量,多次重复,可以把小球的电荷量分为:、、……
最终得出力与电荷量之间的关系:
F
q1q2
带电小球
C
带电小球
A
不带电
平衡小球
B
细银丝
二、库仑的实验
库仑定律的公式
1.公式:
2.比例系数:k=9.0×109
N·m2/C2
这个比例系数叫作静电力常量
3.方向:在两个点电荷的连线上,同种电荷,它们之间的作用力叫作斥力,异种电荷之间的作用力叫作引力。
+
q1
q2
r
F
1
F
2
F
1
+
+
q1
r
F
2
q2
三、静电力的计算
静电力
根据库仑定律得到公式:
比例系数:k=9.0×109
N·m2/C2
这个比例系数叫作静电力常量
根据库仑定律,两个
1C
的点电荷在真空中相距
1m
时,相互作用力是
9.0×109N
,差不多相当于一百多万吨的物体所受的重力,可见库仑是一个非常大的单位。
通常一把梳子和衣服摩擦后所带的电荷量不到百万分之一库仑,闪电产生前,云层积累的电荷量可达几百库仑。
三、静电力的计算
静电力与万有引力
静电力
万有引力
公式
比例系数
静电力常量:
k=9.0×109
N·m2/C2
万有引力常量:
G=6.67×10-11
N·m2/kg2
作用方向
作用力方向在它们的连线上
作用关系
两个点电荷之间的相互作用,可以是引力,也可以是斥力
任意两个物体之间的相互作用,只为引力
相同点
均是与描述的相互作用有关的物理量的乘积成正比;与距离的平方成反比;作用力的方向均在两物体的连线上
三、静电力的计算
静电力与万有引力
例1 在氢原子内,氢原子核与电子之间的最短距离为5.3×10-11m
。试比较氢原子与电子之间的静电力与万有引力。
分析 氢原子核与质子所带的电荷量相同,是1.6×10-19C
。电子带负电,所带的电荷量也是1.6×10-19C
。质子质量为1.6×10-27
kg,电子质量为9.1×10-31
kg
。根据库仑定律和万有引力定律就可以求解。
解 根据库仑定律,它们之间的静电力:
=9.0×109×
N=8.2×10-8
N
三、静电力的计算
静电力与万有引力
根据万有引力定律,它们之间的万有引力
=6.7×10-11×
N=3.6×10-47
N
=2.3×1039
氢原子核与电子之间的静电力是万有引力的
2.3×1039
倍
可见,微观粒子间的万有引力远小于库仑力。因此研究微观粒子的相互作用时,可以忽略万有引力。
三、静电力的计算
多个点电荷间的静电力
库仑定律描述的是两个点电荷之间的相互作用力。如果存在两个以上点电荷,那么,每个点电荷都要受到其他所有点电荷对它的作用力。两个或两个以上点电荷对某一点电荷的作用力,等于各个点电荷单独对这个点电荷的作用力的矢量和。
真空中两个静止的点电荷间的相互作用力的大小只跟两个点电荷的电荷量和间距有关,跟它们的周围是否存在其他点电荷无关。
三、静电力的计算
多个点电荷间的静电力
例2 真空中有三个带正电的点电荷,它们固定在边长为
50cm
的等边三角形的三个顶点上,每个点电荷的电荷量都是
2.0×10-6
C
,求它们各自所受的静电力。
+
+
+
q1
q2
q3
F1
F2
F
分析 根据题目意思作图。每个点电荷都受到其他两个点电荷的斥力,因此,只要求出一个点电荷(例如q3)所受的力即可。
解 根据库仑定律,点电荷
q3
共受到
F1
和
F2
两个力的作用,其中
q1=q2=q3=q
三、静电力的计算
多个点电荷间的静电力
每两个点电荷之间的距离
r
都相同,所以
F1=F2=k
=
N=0.144
N
根据平行四边形定则可得
F=2F1
cos
30°=0.25
N
点电荷
q3
所受的合力
F
的方向为
q1
和
q2
连线的垂直平分线向外。
每个点电荷所受的静电力大小相等,数值均为
0.25
N
,方向均沿另外两个点电荷连线的垂直平分线向外。
库仑定律
静电力:电荷间的相互作用力,又叫库仑力
库仑定律的适用条件:真空两个静止的点电荷间的相互作用力
小结
大小:与它们的电荷量的乘积成正比;与它们距离的平方成反比
方向:在它们的连线上,同性相斥,异性相吸
点电荷:带电体之间的距离远大于它们自身的大小
带电体的大小、形状及电荷分布状况对它们的影响可
以忽略
静电力的计算
公式:
k=9.0×109
N·m2/C2
这个比例系数叫作静电力常量
适用条件:真空两个静止的点电荷
小结
方向:在它们的连线上,同性相斥,异性相吸
两个点电荷间的作用力不会因为第三个点电荷的存在而改变
两个或两个以上点电荷对某一个点电荷的作用力等于各个点电荷单独对这个点电荷的作用力的矢量和
1.下列关于点电荷的说法正确的是
(
)
电荷量很小的带电体就是点电荷
一个电子,不论在任何情况下,都可以看成点电荷
当两个带电体的大小远小于它们之间的距离时,可以将这两个带电体看成点电荷
一切带电体都可以看成点电荷
练习
C
2.有三个完全相同的金属球,球
A
带的电荷量为
q,球
B
和球
C
均不带电。现在要使球
B
带的电荷量为
,应该怎么操作?
练习
答:根据库仑的发现,两个相同的带电金属球接触后所带的电荷量相等。所以,先把球
A
和球
B
接触后分开,此时球
B
带电
q/2;再把球
B
和球
C
接触后分开,则球
B、球
C
分别带电
q/4;最后,球
B
再次与球
A
接触后分开,球
B
带电
qB=
3.半径为
r
的两个金属球,其球心相距
3r,现使两球带上等量的同种电荷
Q,两球之间的静电力
F=k
吗?请说明理由。
练习
答:不等于。因为库仑定律的适用条件是真空中的点电荷,两个半径为
r
的金属球球心相距
3r
时,由于距离太近电荷分布发生变化,两球已经不能视为点电荷,因而它们之间的作用力的大小不能直接用库仑定律进行计算,所以
F
≠
k
4.如图所示,有三个点电荷
A、B、C
位于一个等边三角形的三个顶点上,已知
A、B
都带正电荷,A
所受B、C
两个点电荷的静电力合力如图中
FA
所示,那么可以判断点电荷
C
所带电荷的电性为
(
)
一定是正电
一定是负电
可能是正电,也可能是负电
无法确定
练习
+
+
A
B
C
FA
B
5.在边长为
a
的正方形的每个顶点都放置一个电荷量为
q
的同种点电荷。如果保持它们的位置不变,每个点电荷受到其他三个点电荷的静电力的合力是多少?
练习
答:分析点电荷
q4
的受力情况如右图,q4
共受到三个力的作用,由于q1=q2=q3=q4=q,相互间的距离分别为a、a、a,所以
F1=F3=kF2=k
根据平行四边形定则,合力沿对角线的连线向外,且大小是:
F=2F1cos45°+F2=
由于对称性,每个点电荷受到其他三个电荷的静电力合力的大小都相等,且都沿对角线方向向外。
q4
F3
q1
q2
q3
a
a
a
a
F1
F2
谢谢
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
