《2.3确定圆的条件》同步培优提升训练(Word版 附答案)2021-2022学年九年级数学苏科版上册
文档属性
| 名称 | 《2.3确定圆的条件》同步培优提升训练(Word版 附答案)2021-2022学年九年级数学苏科版上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览





文档简介
2021-2022学年苏科版九年级数学上册《2.3确定圆的条件》同步培优提升训练(附答案)
一.选择题(共8小题)
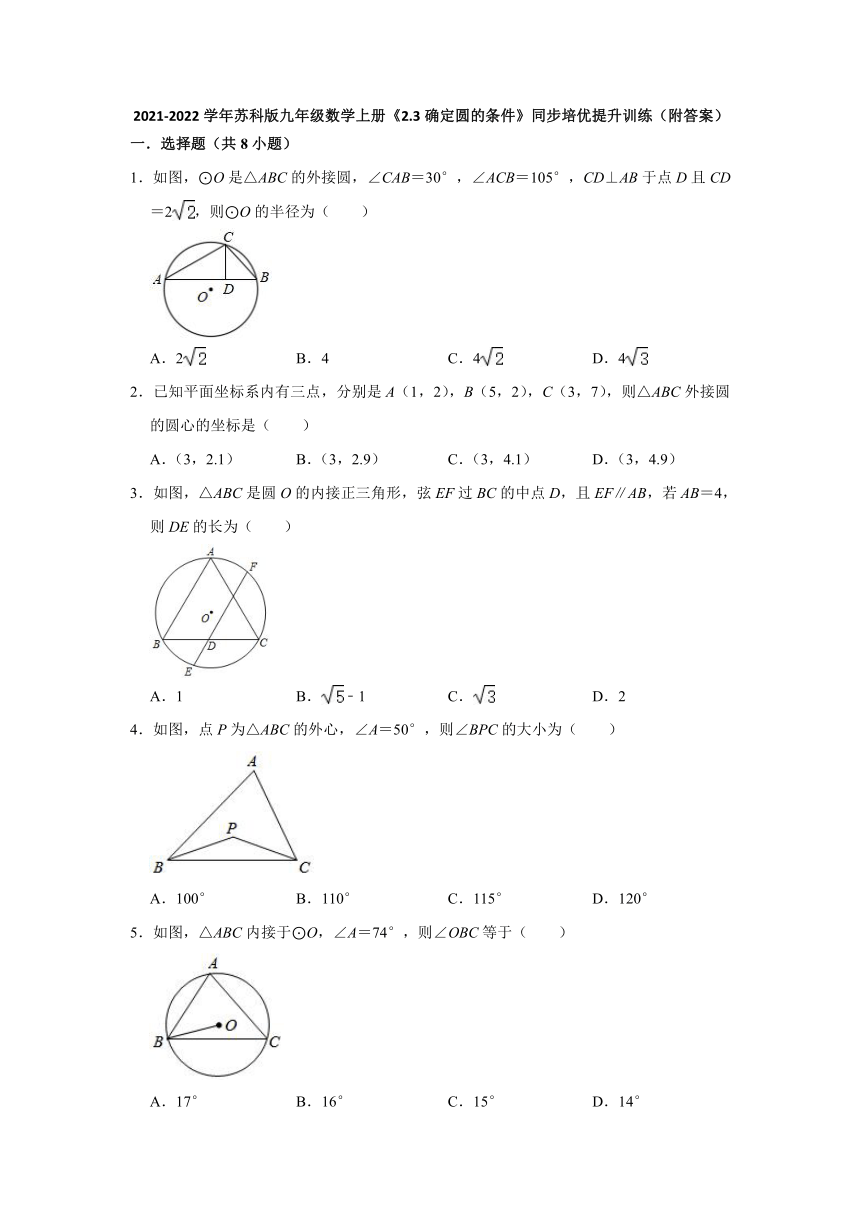
1.如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2
B.4
C.4
D.4
2.已知平面坐标系内有三点,分别是A(1,2),B(5,2),C(3,7),则△ABC外接圆的圆心的坐标是( )
A.(3,2.1)
B.(3,2.9)
C.(3,4.1)
D.(3,4.9)
3.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1
B.﹣1
C.
D.2
4.如图,点P为△ABC的外心,∠A=50°,则∠BPC的大小为( )
A.100°
B.110°
C.115°
D.120°
5.如图,△ABC内接于⊙O,∠A=74°,则∠OBC等于( )
A.17°
B.16°
C.15°
D.14°
6.如图,△ABC内接于⊙O,且⊙O的半径为2,若∠ACB=45°,则AB为( )
A.2
B.
C.4
D.2
7.在Rt△ABC中,∠C=90°,AC=20厘米,BC=21厘米,则它的外心与顶点C的距离等于( )
A.13厘米
B.13.5厘米
C.14厘米
D.14.5厘米
8.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.①
B.②
C.③
D.④
二.填空题(共8小题)
9.△ABC中,AB=9cm,AC=40cm,BC=41cm,则△ABC的外接圆半径长是
.
10.三角形的三个顶点都在同一个圆上,则这个圆的圆心是这个三角形三条边的
的交点.
11.⊙O的半径为5,△ABC内接于⊙O,AB=AC,BC=6,则△ABC的面积是
.
12.某园林单位要在一个绿化带内开挖一个△ABC的工作面,使得∠ACB=60°,CD是AB边上的高,且CD=6,则△ABC的面积最小值是
.
13.如图,⊙O是△ABC的外接圆,∠COB=60°,AB=BC=3,则弦AC=
.
14.如图,△ABC内接于⊙O,点M,N分别是CO,AB的中点,∠CAB=80°,∠CBA=40°,则∠OMN的度数是
.
15.如图,小方格边长为1,则△ABC的外心的坐标是
.
16.如图所示,已知△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若BC=5,则OD=
.
三.解答题(共4小题)
17.如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长交边AC于点D.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小.
18.已知等腰△ABC的底边长为3,两腰长恰好是关于x的一元二次方程kx2﹣(k+3)x+6=0的两根,
(1)求△ABC的周长;
(2)如果⊙O是△ABC的外接圆,求⊙O的半径.
19.如图,⊙O是△ABC的外接圆,AB长为4,AB=AC,联结CO并延长,交边AB于点D,交AB于点E,且E为弧AB的中点.求:
(1)边BC的长;
(2)⊙O的半径.
20.如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,点M从C点开始以1cm/s的速度沿CB向B点运动,点N从A点开始以2cm/s的速度沿AC向C点运动,点M、N同时出发,当一个点到达终点时,另一个点也停止运动.
(1)2秒时,△MCN的面积是
;
(2)求经过几秒,△MCN的面积是3cm2;
(3)试说明△MCN外接圆的半径能否是cm.
参考答案
一.选择题(共8小题)
1.解:如图,连接OA,OC,
∵CD⊥AB,
∴∠ADC=90°,
∵∠CAB=30°,CD=2,
∴AC=2CD=4,
∵∠ACB=105°,∠ACD=60°,
∴∠CBA=45°,
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,由勾股定理得:AC2=OA2+OC2,
∵OA=OC,
∴OA=AC=4,
∴⊙O的半径为4,
故选:B.
2.解:如图,设△ABC外接圆的圆心为O′,
∵A(1,2),B(5,2),C(3,7),
∴△ABC是等腰三角形,
∴AE=BE=AB=4=2,CD=7,DE=2,
设O′A=O′B=x,则O′E=CD﹣O′C﹣DE=7﹣x﹣2=5﹣x,
在Rt△O′AE中,根据勾股定理,得
O′A2=O′E2+AE2,
∴x2=(5﹣x)2+22,
解得x=2.9,
∴O′E=5﹣x=2.1,
∴O′D=O′E+DE=2.1+2=4.1,
∴△ABC外接圆的圆心O′的坐标是(3,4.1).
故选:C.
3.解:如图.过C作CN⊥AB于N,交EF于M,
∵EF∥AB,
∴CM⊥EF.
根据圆和等边三角形的性质知:CN必过点O.
∵EF∥AB,D是BC的中点,
∴DG是△ABC的中位线,
∴DG=AB=2;
∵△CGD是等边三角形,CM⊥DG,
∴DM=MG;
∵OM⊥EF,由垂径定理得:EM=MF,
∴DE=GF.
∵弦BC、EF相交于点D,
∴BD?DC=DE?DF,即DE×(DE+2)=4;
解得DE=﹣1(负值舍去).
故选:B.
4.解:∵∠BPC=2∠A,∠A=50°,P为△ABC的外心,
∴∠BPC=100°.
故选:A.
5.解:如图,连接OC,
∵∠A=74°,
∴∠BOC=2∠A=148°,
∵OB=OC,
∴∠OBC=∠OCB=(180°﹣148°)=16°.
故选:B.
6.解:如图,连接OA,OB,
∵∠ACB=45°,
∴∠AOB=90°,
∵OA=OB=2,
∴AB==2,
故选:D.
7.解:如图,取AB的中点O,连接OC,
∴OC==OA=OB,
∴A,B,C在以O为圆心,OC为半径的圆上,
∴O是△ABC的外心,
在Rt△ABC中,
AB==29厘米,
∴=14.5厘米,
故选:D.
8.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
二.填空题(共8小题)
9.解:在△ABC中,AB=9cm,AC=40cm,BC=41cm,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,且AB是斜边,
∴△ABC的外接圆半径长为:AB=20.5cm.
故答案为:20.5cm.
10.解:设△ABC的三个顶点均在⊙O上,
连接OA,OB,OC,如图,
∵OA=OB,
∴O在边AB的垂直平分线上,
同理,O在边BC的垂直平分线上,O在边AC的垂直平分线上,
∴O是三角形三条边的垂直平分线的交点,
故答案为:垂直平分线.
11.解:如图1,当圆心在△ABC外时,
连接AO交BC于H,连接OC,
∵AB=AC,
∴=,
∴AH⊥BC,
∴∠CHO=90°,CH=BC=3,
∵OC=5,
∴OH==4,
∴AH=OA﹣OH=1,
∴△ABC的面积=AH?BC=1×6=3;
如图2,当圆心在△ABC内时,
连接AO并延长交BC于H,连接OC,
∵AB=AC,
∴=,
∴AH⊥BC,
∴∠CHO=90°,CH=BC=3,
∵OC=5,
∴OH==4,
∴AH=OA+OH=9,
∴△ABC的面积=AH?BC=6×9=27;
综上所述,△ABC的面积是3或27,
故答案为:3或27.
12.解:作△ABC的外接圆⊙O,连接OA、OB、OC,作OE⊥AB于E,设OA=OC=2x.
∵∠AOC=2∠ACB,∠ACB=60°,
∴∠AOB=120°,∠ACB=60°,OA=OB=R,OE⊥AB,
∴AE=EB,∠AOE=∠BOE=60°,
∴OE=OA=x,AE=x,
∵OC+OE≥CD,CD=6,
∴3x≥6,
∴x≥2,
∴x的最小值为2.
∵E为AB中点,
∴AB=AE+BE=2AE=2x,
∵AB的最小值为4,
∴S△ABC的最小值===12.
故答案为:12.
13.解:设OB与AC交于点D,
∵∠COB=60°,AB=BC,
∴△COB为等边三角形,
∴OC=BC=3,
∵AB=BC,
∴=,
∴OD⊥AC,CD=AD,
∴CD=,
∴AC=3,
故答案为:3.
14.解:如图,连接OA,OB,ON,取OA的中点D,连接DN,
∵∠CAB=80°,∠CBA=40°,
∴∠ACB=180°﹣∠CAB﹣∠CBA=180°﹣80°﹣40°=60°,
∴∠AOB=120°,∠AOC=80°,
∵点M是OC的中点,点D是OA的中点,
∴OD=OM=OA,
∵点N是AB的中点,且∠AOB=120°,
∴ON⊥AB,∠AON=∠BON=60°,
∵点D是OA的中点,且∠ONA=90°,
∴DN=DO,
∴△ODN是等边三角形,
∴OD=OA,
∴OD=ON=OM,
∵∠MON=∠COA+∠AON=80°+60°=140°,
∴∠OMN=∠NOM==20°.
故答案为:20°.
15.解:如图所示:△ABC的外心坐标是P(﹣2,﹣1).
故答案为:(﹣2,﹣1).
16.解:∵BC是⊙O的直径,
∴∠BAC=90°,
∵OE⊥BC,
∴∠BOE=∠COE=90°,
∴=,
∴∠BAE=∠CAE=∠BAC=×90°=45°,
∵EA⊥BD,
∴∠ABD=∠ADB=45°,
∴AD=AB,
∵OD⊥AC,
∴DC=AD,
设AB=x,则AC=2x,
∵BC=5,AB2+AC2=BC2,
∴x2+(2x)2=52,
解得x=.
∴AB=.
∵OD⊥AC,AB⊥AC,
∴OD∥AB,
∵BO=CO,
∴OD=AB=,
故答案为:.
三.解答题(共4小题)
17.解(1)连接OA并延长AO交BC于E,
∵AB=AC,
∴弧AB=弧AC,
∵AE过圆心O,
∴AE垂直平分BC(平分弧的直径垂直平分弧所对的弦),
∴AE平分∠BAC,
∴∠BAC=2∠BAE,
∵OA=OB,
∴∠ABD=∠BAE,
∴∠BAC=2∠ABD;
(2)设∠ABD=x,
由(1)知∠BAC=2∠ABD=2x,
∴∠BDC=3x,
△BCD是等腰三角形,
①若BD=BC,
则∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴3x+3x+2x=180°,
解得x=22.5°,
∴∠BCD=3x=67.5°,
②若BC=CD,则∠BDC=∠CBD=3x,
∴∠ABC=∠ACB=4x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴4x+4x+2x=180°,
∴x=18°,
∴∠BCD=4x=72°,
综上所述,△BCD是等腰三角形,∠BCD为67.5°或72°.
18.解:(1)∵两腰长恰好是关于x的一元二次方程kx2﹣(k+3)x+6=0的两根,
∴△=[﹣(k+3)]2﹣4×k×6=0,
解得k=3,
∴一元二次方程为x2﹣6x+6=0,
∴两腰之和为=4,
∴△ABC的周长为4+3=7;
(2)如图,连接OB,OC,连接AO并延长交BC于D,
∵AB=AC=2,OB=OC,
∴AD⊥BC,BD=CD=BC=1.5,
∴AD===,
设AO=OB=r,
∴OD=﹣r,
∵OB2=OD2+BD2,
∴r2=(﹣r)2+()2,
∴r=,
∴⊙O的半径为.
19.解:(1)∵E点为的中点,CE为直径,
∴CE⊥AB,
∴AD=BD,
即CD垂直平分AB,
∴CB=CA=4;
(2)连接OB,如图,
∵AB=BC=AC,
∴△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴∠BOD=60°,
在Rt△BOD中,BD=AB=2,
∴OD=BD=,
∴OB=2OD=,
即⊙O的半径为.
20.解:(1)∵∠C=90°,AB=10cm,BC=6cm,
∴AC==8,
根据题意得,AN=4,CM=2,
∴CN=4,
∴S△CMN=×4×2=4(cm2);
故答案为4cm2;
(2)设经过x秒,
根据题意得,(8﹣2x)?x=3,
解得x1=1,x2=3;
即经过1秒或3秒,△MCN的面积是3cm2;
(3)∵△MNC为直角三角形,∠C=90°,
∴MN为△MCN外接圆的直径,
假设△MCN外接圆的半径为cm,则MN=2cm,
设M点运动的时间为t秒,则NC=8﹣2t,CM=t,
根据题意得,(8﹣2t)2+t2=(2)2,
整理得5t2﹣32t+52=0,
∵△=(﹣32)2﹣4×5×52=﹣16<0,
∴原方程没有实数解,
∴△MCN外接圆的半径不能是cm.
一.选择题(共8小题)
1.如图,⊙O是△ABC的外接圆,∠CAB=30°,∠ACB=105°,CD⊥AB于点D且CD=2,则⊙O的半径为( )
A.2
B.4
C.4
D.4
2.已知平面坐标系内有三点,分别是A(1,2),B(5,2),C(3,7),则△ABC外接圆的圆心的坐标是( )
A.(3,2.1)
B.(3,2.9)
C.(3,4.1)
D.(3,4.9)
3.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1
B.﹣1
C.
D.2
4.如图,点P为△ABC的外心,∠A=50°,则∠BPC的大小为( )
A.100°
B.110°
C.115°
D.120°
5.如图,△ABC内接于⊙O,∠A=74°,则∠OBC等于( )
A.17°
B.16°
C.15°
D.14°
6.如图,△ABC内接于⊙O,且⊙O的半径为2,若∠ACB=45°,则AB为( )
A.2
B.
C.4
D.2
7.在Rt△ABC中,∠C=90°,AC=20厘米,BC=21厘米,则它的外心与顶点C的距离等于( )
A.13厘米
B.13.5厘米
C.14厘米
D.14.5厘米
8.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.①
B.②
C.③
D.④
二.填空题(共8小题)
9.△ABC中,AB=9cm,AC=40cm,BC=41cm,则△ABC的外接圆半径长是
.
10.三角形的三个顶点都在同一个圆上,则这个圆的圆心是这个三角形三条边的
的交点.
11.⊙O的半径为5,△ABC内接于⊙O,AB=AC,BC=6,则△ABC的面积是
.
12.某园林单位要在一个绿化带内开挖一个△ABC的工作面,使得∠ACB=60°,CD是AB边上的高,且CD=6,则△ABC的面积最小值是
.
13.如图,⊙O是△ABC的外接圆,∠COB=60°,AB=BC=3,则弦AC=
.
14.如图,△ABC内接于⊙O,点M,N分别是CO,AB的中点,∠CAB=80°,∠CBA=40°,则∠OMN的度数是
.
15.如图,小方格边长为1,则△ABC的外心的坐标是
.
16.如图所示,已知△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若BC=5,则OD=
.
三.解答题(共4小题)
17.如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长交边AC于点D.
(1)求证:∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时,求∠BCD的大小.
18.已知等腰△ABC的底边长为3,两腰长恰好是关于x的一元二次方程kx2﹣(k+3)x+6=0的两根,
(1)求△ABC的周长;
(2)如果⊙O是△ABC的外接圆,求⊙O的半径.
19.如图,⊙O是△ABC的外接圆,AB长为4,AB=AC,联结CO并延长,交边AB于点D,交AB于点E,且E为弧AB的中点.求:
(1)边BC的长;
(2)⊙O的半径.
20.如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,点M从C点开始以1cm/s的速度沿CB向B点运动,点N从A点开始以2cm/s的速度沿AC向C点运动,点M、N同时出发,当一个点到达终点时,另一个点也停止运动.
(1)2秒时,△MCN的面积是
;
(2)求经过几秒,△MCN的面积是3cm2;
(3)试说明△MCN外接圆的半径能否是cm.
参考答案
一.选择题(共8小题)
1.解:如图,连接OA,OC,
∵CD⊥AB,
∴∠ADC=90°,
∵∠CAB=30°,CD=2,
∴AC=2CD=4,
∵∠ACB=105°,∠ACD=60°,
∴∠CBA=45°,
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,由勾股定理得:AC2=OA2+OC2,
∵OA=OC,
∴OA=AC=4,
∴⊙O的半径为4,
故选:B.
2.解:如图,设△ABC外接圆的圆心为O′,
∵A(1,2),B(5,2),C(3,7),
∴△ABC是等腰三角形,
∴AE=BE=AB=4=2,CD=7,DE=2,
设O′A=O′B=x,则O′E=CD﹣O′C﹣DE=7﹣x﹣2=5﹣x,
在Rt△O′AE中,根据勾股定理,得
O′A2=O′E2+AE2,
∴x2=(5﹣x)2+22,
解得x=2.9,
∴O′E=5﹣x=2.1,
∴O′D=O′E+DE=2.1+2=4.1,
∴△ABC外接圆的圆心O′的坐标是(3,4.1).
故选:C.
3.解:如图.过C作CN⊥AB于N,交EF于M,
∵EF∥AB,
∴CM⊥EF.
根据圆和等边三角形的性质知:CN必过点O.
∵EF∥AB,D是BC的中点,
∴DG是△ABC的中位线,
∴DG=AB=2;
∵△CGD是等边三角形,CM⊥DG,
∴DM=MG;
∵OM⊥EF,由垂径定理得:EM=MF,
∴DE=GF.
∵弦BC、EF相交于点D,
∴BD?DC=DE?DF,即DE×(DE+2)=4;
解得DE=﹣1(负值舍去).
故选:B.
4.解:∵∠BPC=2∠A,∠A=50°,P为△ABC的外心,
∴∠BPC=100°.
故选:A.
5.解:如图,连接OC,
∵∠A=74°,
∴∠BOC=2∠A=148°,
∵OB=OC,
∴∠OBC=∠OCB=(180°﹣148°)=16°.
故选:B.
6.解:如图,连接OA,OB,
∵∠ACB=45°,
∴∠AOB=90°,
∵OA=OB=2,
∴AB==2,
故选:D.
7.解:如图,取AB的中点O,连接OC,
∴OC==OA=OB,
∴A,B,C在以O为圆心,OC为半径的圆上,
∴O是△ABC的外心,
在Rt△ABC中,
AB==29厘米,
∴=14.5厘米,
故选:D.
8.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
二.填空题(共8小题)
9.解:在△ABC中,AB=9cm,AC=40cm,BC=41cm,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,且AB是斜边,
∴△ABC的外接圆半径长为:AB=20.5cm.
故答案为:20.5cm.
10.解:设△ABC的三个顶点均在⊙O上,
连接OA,OB,OC,如图,
∵OA=OB,
∴O在边AB的垂直平分线上,
同理,O在边BC的垂直平分线上,O在边AC的垂直平分线上,
∴O是三角形三条边的垂直平分线的交点,
故答案为:垂直平分线.
11.解:如图1,当圆心在△ABC外时,
连接AO交BC于H,连接OC,
∵AB=AC,
∴=,
∴AH⊥BC,
∴∠CHO=90°,CH=BC=3,
∵OC=5,
∴OH==4,
∴AH=OA﹣OH=1,
∴△ABC的面积=AH?BC=1×6=3;
如图2,当圆心在△ABC内时,
连接AO并延长交BC于H,连接OC,
∵AB=AC,
∴=,
∴AH⊥BC,
∴∠CHO=90°,CH=BC=3,
∵OC=5,
∴OH==4,
∴AH=OA+OH=9,
∴△ABC的面积=AH?BC=6×9=27;
综上所述,△ABC的面积是3或27,
故答案为:3或27.
12.解:作△ABC的外接圆⊙O,连接OA、OB、OC,作OE⊥AB于E,设OA=OC=2x.
∵∠AOC=2∠ACB,∠ACB=60°,
∴∠AOB=120°,∠ACB=60°,OA=OB=R,OE⊥AB,
∴AE=EB,∠AOE=∠BOE=60°,
∴OE=OA=x,AE=x,
∵OC+OE≥CD,CD=6,
∴3x≥6,
∴x≥2,
∴x的最小值为2.
∵E为AB中点,
∴AB=AE+BE=2AE=2x,
∵AB的最小值为4,
∴S△ABC的最小值===12.
故答案为:12.
13.解:设OB与AC交于点D,
∵∠COB=60°,AB=BC,
∴△COB为等边三角形,
∴OC=BC=3,
∵AB=BC,
∴=,
∴OD⊥AC,CD=AD,
∴CD=,
∴AC=3,
故答案为:3.
14.解:如图,连接OA,OB,ON,取OA的中点D,连接DN,
∵∠CAB=80°,∠CBA=40°,
∴∠ACB=180°﹣∠CAB﹣∠CBA=180°﹣80°﹣40°=60°,
∴∠AOB=120°,∠AOC=80°,
∵点M是OC的中点,点D是OA的中点,
∴OD=OM=OA,
∵点N是AB的中点,且∠AOB=120°,
∴ON⊥AB,∠AON=∠BON=60°,
∵点D是OA的中点,且∠ONA=90°,
∴DN=DO,
∴△ODN是等边三角形,
∴OD=OA,
∴OD=ON=OM,
∵∠MON=∠COA+∠AON=80°+60°=140°,
∴∠OMN=∠NOM==20°.
故答案为:20°.
15.解:如图所示:△ABC的外心坐标是P(﹣2,﹣1).
故答案为:(﹣2,﹣1).
16.解:∵BC是⊙O的直径,
∴∠BAC=90°,
∵OE⊥BC,
∴∠BOE=∠COE=90°,
∴=,
∴∠BAE=∠CAE=∠BAC=×90°=45°,
∵EA⊥BD,
∴∠ABD=∠ADB=45°,
∴AD=AB,
∵OD⊥AC,
∴DC=AD,
设AB=x,则AC=2x,
∵BC=5,AB2+AC2=BC2,
∴x2+(2x)2=52,
解得x=.
∴AB=.
∵OD⊥AC,AB⊥AC,
∴OD∥AB,
∵BO=CO,
∴OD=AB=,
故答案为:.
三.解答题(共4小题)
17.解(1)连接OA并延长AO交BC于E,
∵AB=AC,
∴弧AB=弧AC,
∵AE过圆心O,
∴AE垂直平分BC(平分弧的直径垂直平分弧所对的弦),
∴AE平分∠BAC,
∴∠BAC=2∠BAE,
∵OA=OB,
∴∠ABD=∠BAE,
∴∠BAC=2∠ABD;
(2)设∠ABD=x,
由(1)知∠BAC=2∠ABD=2x,
∴∠BDC=3x,
△BCD是等腰三角形,
①若BD=BC,
则∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴3x+3x+2x=180°,
解得x=22.5°,
∴∠BCD=3x=67.5°,
②若BC=CD,则∠BDC=∠CBD=3x,
∴∠ABC=∠ACB=4x,
在△ABC中,∠ABC+∠C+∠BAC=180°,
∴4x+4x+2x=180°,
∴x=18°,
∴∠BCD=4x=72°,
综上所述,△BCD是等腰三角形,∠BCD为67.5°或72°.
18.解:(1)∵两腰长恰好是关于x的一元二次方程kx2﹣(k+3)x+6=0的两根,
∴△=[﹣(k+3)]2﹣4×k×6=0,
解得k=3,
∴一元二次方程为x2﹣6x+6=0,
∴两腰之和为=4,
∴△ABC的周长为4+3=7;
(2)如图,连接OB,OC,连接AO并延长交BC于D,
∵AB=AC=2,OB=OC,
∴AD⊥BC,BD=CD=BC=1.5,
∴AD===,
设AO=OB=r,
∴OD=﹣r,
∵OB2=OD2+BD2,
∴r2=(﹣r)2+()2,
∴r=,
∴⊙O的半径为.
19.解:(1)∵E点为的中点,CE为直径,
∴CE⊥AB,
∴AD=BD,
即CD垂直平分AB,
∴CB=CA=4;
(2)连接OB,如图,
∵AB=BC=AC,
∴△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴∠BOD=60°,
在Rt△BOD中,BD=AB=2,
∴OD=BD=,
∴OB=2OD=,
即⊙O的半径为.
20.解:(1)∵∠C=90°,AB=10cm,BC=6cm,
∴AC==8,
根据题意得,AN=4,CM=2,
∴CN=4,
∴S△CMN=×4×2=4(cm2);
故答案为4cm2;
(2)设经过x秒,
根据题意得,(8﹣2x)?x=3,
解得x1=1,x2=3;
即经过1秒或3秒,△MCN的面积是3cm2;
(3)∵△MNC为直角三角形,∠C=90°,
∴MN为△MCN外接圆的直径,
假设△MCN外接圆的半径为cm,则MN=2cm,
设M点运动的时间为t秒,则NC=8﹣2t,CM=t,
根据题意得,(8﹣2t)2+t2=(2)2,
整理得5t2﹣32t+52=0,
∵△=(﹣32)2﹣4×5×52=﹣16<0,
∴原方程没有实数解,
∴△MCN外接圆的半径不能是cm.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
