2.1.1圆的概念、点和圆的位置关系-2021-2022学年苏科版九年级数学上册培优训练(Word版 含答案)
文档属性
| 名称 | 2.1.1圆的概念、点和圆的位置关系-2021-2022学年苏科版九年级数学上册培优训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 317.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览




文档简介
2.1.1圆的概念、点和圆的位置关系
-2021-2022学年苏科版九年级数学上册
培优训练
一、选择题
1、下列条件能确定圆的是(
)
A.以O为圆心的圆
B.以2
cm为半径的圆
C.经过已知点A的圆
D.以点O为圆心,以1
cm为半径的圆
2、已知⊙O的半径是4,OA=3,则点A与⊙O的位置关系是( )
A.点A在圆内
B.点A在圆上
C.点A在圆外
D.无法确定
3、⊙O的半径为3cm,若点P在⊙O内,则OP的长可能是( )
A.2cm
B.3cm
C.4cm
D.5cm
4、⊙O的半径为5,点A到圆心O的距离为d,已知点A在⊙O的外部,则( )
A.d<5
B.d>5
C.d≥5
D.d=5
5、若⊙O的半径为5,点P到圆心的距离为d,当点P在圆上时,则有(
)
A.d<5
B.d>5
C.d
=
5
D.d
=
6、已知⊙O的半径OA长为1,OB,则可以得到的正确图形可能是( )
A.B.
C.D.
7、若点A在⊙O内,点B在⊙O外,OA=3,OB=5,则⊙O的半径r的取值范围是(
)
A.0<r<3
B.2<r<8
C.3<r<5
D.r>5
8、已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内
B.在⊙O外
C.在⊙O上
D.无法确定
9、已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2﹣2x+d=0有实根,则点P( )
A.在⊙O的内部
B.在⊙O的外部
C.在⊙O上
D.在⊙O上或⊙O的内部
10、如图,在中,,,,点E是中点.以B为圆心,为半径画圆,则点E与的位置关系是(
)
A.点E在内
B.点E在上
C.点E在外
D.无法判断
二、填空题
11、到定点O的距离等于4的点的集合是
.
12、已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A在⊙O (填“上”“外”或“内”)
13、已知⊙O的半径为6cm,当OP=6cm时,点P在
;当OP
时,点P在圆内;当OP
时,点P不在圆外.
14、在平面内,⊙O的半径为2cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .
15、已知圆O的半径为5,P是线段OA的中点,若OA=10,则点P在⊙O ,点A在⊙O .
16、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
,点B在⊙C
.
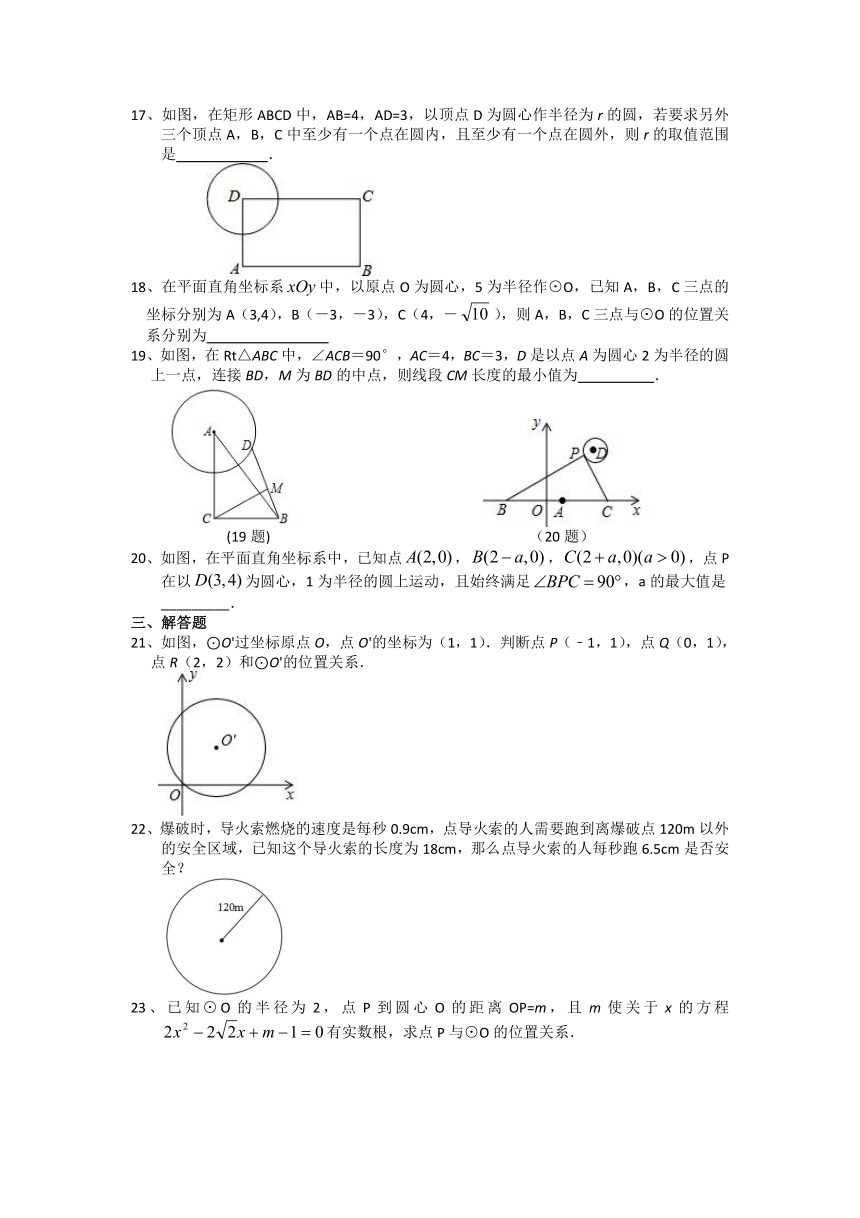
17、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
.
18、在平面直角坐标系中,以原点O为圆心,5为半径作⊙O,已知A,B,C三点的坐标分别为A(3,4),B(-3,-3),C(4,-),则A,B,C三点与⊙O的位置关系分别为
19、如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最小值为
.
(19题)
(20题)
20、如图,在平面直角坐标系中,已知点,,,点P在以为圆心,1为半径的圆上运动,且始终满足,a的最大值是_________.
三、解答题
21、如图,⊙O'过坐标原点O,点O'的坐标为(1,1).判断点P(﹣1,1),点Q(0,1),点R(2,2)和⊙O'的位置关系.
22、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,那么点导火索的人每秒跑6.5cm是否安全?
23、已知⊙O的半径为2,点P到圆心O的距离OP=m,且m使关于x的方程有实数根,求点P与⊙O的位置关系.
24、如图,已知BD、CE是△ABC的高,M是BC的中点,则点B,C,D,E是否在以点M为圆心的圆上?为什么?
25、在中,AB=3厘米,BC=4厘米,CA=5厘米.
(1)以点A为圆心,以3厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(2)以点A为圆心,以4厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(3)以点B为圆心,以4厘米长为半径画圆,确定点A,C与⊙B的位置关系.
2.1.1圆的概念、点和圆的位置关系
-2021-2022学年苏科版九年级数学上册
培优训练(答案)
一、选择题
1、下列条件能确定圆的是(
)
A.以O为圆心的圆
B.以2
cm为半径的圆
C.经过已知点A的圆
D.以点O为圆心,以1
cm为半径的圆
【答案】D
【解析】解:由圆的概念可知,确定一个圆有两个要素:圆心和半径,两者缺一不可,由此可得:A只有圆心,错误;B只有半径,错误;C经过已知点A的圆,圆心和半径都不确定,错误;D确定了圆心和半径,正确.故选D
.
2、已知⊙O的半径是4,OA=3,则点A与⊙O的位置关系是( )
A.点A在圆内
B.点A在圆上
C.点A在圆外
D.无法确定
【分析】根据⊙O的半径r=4,且点A到圆心O的距离d=3知d<r,据此可得答案.
【解析】∵⊙O的半径r=4,且点A到圆心O的距离d=3,
∴d<r,
∴点A在⊙O内,
故选:A.
3、⊙O的半径为3cm,若点P在⊙O内,则OP的长可能是( )
A.2cm
B.3cm
C.4cm
D.5cm
【分析】根据点在圆内,点到圆心的距离小于圆的半径进行判断.
【解答】解⊙O的半径为3cm,点P在⊙O内,
∴OP<3cm.
故选:A.
4、⊙O的半径为5,点A到圆心O的距离为d,已知点A在⊙O的外部,则( )
A.d<5
B.d>5
C.d≥5
D.d=5
【分析】根据点与圆的位置关系判断得出即可.
【解析】∵点A在圆O的外部,圆O的半径为5,
∴点A到圆心O的距离d的范围是:d>5.
故选:B.
5、若⊙O的半径为5,点P到圆心的距离为d,当点P在圆上时,则有(
)
A.d<5
B.d>5
C.d
=
5
D.d
=
【答案】C由于点P在圆上,所以点P到圆心的距离等于圆的半径,即d=5.故选:C.
6、已知⊙O的半径OA长为1,OB,则可以得到的正确图形可能是( )
A.B.
C.D.
【分析】根据点到圆心的距离和圆的半径的大小关系判断点与圆的位置关系即可.
【解析】∵⊙O的半径OA长1,若OB,
∴OA<OB,∴点B在圆外,
故选:D.
7、若点A在⊙O内,点B在⊙O外,OA=3,OB=5,则⊙O的半径r的取值范围是(
)
A.0<r<3
B.2<r<8
C.3<r<5
D.r>5
【答案】C
【解析】解:∵点A在半径为r的⊙O内,点B在⊙O外,
∴OA小于r,OB大于r,
∵OA=3,OB=5,∴3<r<5.故选:C.
8、已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内
B.在⊙O外
C.在⊙O上
D.无法确定
【分析】关于x的方程x2﹣2dx+1=0有两个相等的实数根,即判别式△=b2﹣4ac=0.即可得到关于d的不等式,从而求得d的范围,进而判断点A与⊙O的位置关系.
【解析】∵a=1,b=﹣2d,c=1,
∴△=b2﹣4ac=(﹣2d)2﹣4×1×1=4d2﹣4=0,
解得:d=1.
则点A在⊙O上.
故选:C.
9、已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2﹣2x+d=0有实根,则点P( )
A.在⊙O的内部
B.在⊙O的外部
C.在⊙O上
D.在⊙O上或⊙O的内部
【分析】首先根据关于x的方程有实数根求得d的取值范围,然后利用d与半径的大小关系判断点与圆的位置关系.
【解析】∵关于x的方程x2﹣2x+d=0有实根,∴根的判别式△=(﹣2)2﹣4×d≥0,解得d≤1,
∴点在圆内或在圆上,
故选:D.
10、如图,在中,,,,点E是中点.以B为圆心,为半径画圆,则点E与的位置关系是(
)
A.点E在内
B.点E在上
C.点E在外
D.无法判断
【答案】A
【解析】解:在Rt△ABC中,∠C=90°,AC=4,BC=3,
由勾股定理得到:
∵E为AB的中点,∴BE=AB=2.5.
∵BC=3,∴BE<BC,∴点E在⊙B的内部,故选:A.
二、填空题
11、到定点O的距离等于4的点的集合是
.
【答案】以定点O为圆心,4为半径的圆
12、已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A在⊙O (填“上”“外”或“内”)
【解答】解:∵OA=3cm<4cm∴点A在⊙O内.
故答案是:内.
13、已知⊙O的半径为6cm,当OP=6cm时,点P在
;当OP
时,点P在圆内;当OP
时,点P不在圆外.
【答案】圆上;<6cm;≤6cm
14、在平面内,⊙O的半径为2cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .
【解答】解:∵⊙O的半径为2cm,点P到圆心O的距离为3cm,
∴d>r,
∴点P与⊙O的位置关系是:P在⊙O外.
故答案为:点P在圆外
15、已知圆O的半径为5,P是线段OA的中点,若OA=10,则点P在⊙O ,点A在⊙O .
【解答】解:∵P为OA的中点,
∴OP=OA=5,
∴OP=r=5,
∴点P在⊙O上;
∵OA=10>r,
∴点A在圆外.
故答案为上,外;
16、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
,点B在⊙C
.
【答案】上;外
17、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
.
【答案】318、在平面直角坐标系中,以原点O为圆心,5为半径作⊙O,已知A,B,C三点的坐标分别为A(3,4),B(-3,-3),C(4,-),则A,B,C三点与⊙O的位置关系分别为
【答案】点A在⊙O上,点B在⊙O内,点C在⊙O外
19、如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最小值为
.
【分析】作AB的中点E,连接EM、CE,根据直角三角形斜边上的中线等于斜边的一半以及三角形的中位线定理求得CE和EM的长,然后确定CM的范围.
【解析】作AB的中点E,连接EM、CE.
在直角△ABC中,
∵E是直角△ABC斜边AB上的中点,∴CE=AB=2.5.
∵M是BD的中点,E是AB的中点,∴ME=AD=1.
∵2.5﹣1≤CM≤2.5+1,即1.5≤CM≤3.5.∴最小值为1.5,
故答案为:1.5.
20、如图,在平面直角坐标系中,已知点,,,点P在以为圆心,1为半径的圆上运动,且始终满足,a的最大值是_________.
【答案】1+.
【解析】解:连接PA,
∵A(2,0),B(2?a,0),C(2+a,0),
∴AB=AC=a,
∵∠BPC=90°,∴PA=AB=AC=a,
∵DA=,
∴点P为直线AD与圆的交点重合时,a取最大和最小值,即:a的最大值=1+.
故答案为:1+.
三、解答题
21、如图,⊙O'过坐标原点O,点O'的坐标为(1,1).判断点P(﹣1,1),点Q(0,1),点R(2,2)和⊙O'的位置关系.
【解答】解:圆的半径是,
PO′=2>,则P在⊙O′的外部;
QO′=1<,则Q在⊙O′的内部;
RO′==圆的半径,故R在圆上.
22、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,那么点导火索的人每秒跑6.5cm是否安全?
解:点导火索的人安全。
导火索燃烧的时间为:,
此时点导火索的人跑的路程为
因为130>120,所以点导火索的人安全。
23、已知⊙O的半径为2,点P到圆心O的距离OP=m,且m使关于x的方程有实数根,求点P与⊙O的位置关系.
【答案】点P在圆上或圆内
解:=,
,即
∴点P在圆上或圆内
24、如图,已知BD、CE是△ABC的高,M是BC的中点,则点B,C,D,E是否在以点M为圆心的圆上?为什么?
解:点B,C,D,E在以点M为圆心的圆上
连接ME,MD,
∵RtBEC、RtBDC中,M是BC的中点,
,
∴点B,C,D,E在以点M为圆心的圆上
25、在中,AB=3厘米,BC=4厘米,CA=5厘米.
(1)以点A为圆心,以3厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(2)以点A为圆心,以4厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(3)以点B为圆心,以4厘米长为半径画圆,确定点A,C与⊙B的位置关系.
解:如图,以点A为圆心,以3厘米长为半径画圆,点B在上,点C在外.
如图,以点A为圆心,以4厘米长为半径画圆,点B在内,C在外.
如图,以点B为圆心,以4厘米长为半径画圆,点A在内,C与上.
-2021-2022学年苏科版九年级数学上册
培优训练
一、选择题
1、下列条件能确定圆的是(
)
A.以O为圆心的圆
B.以2
cm为半径的圆
C.经过已知点A的圆
D.以点O为圆心,以1
cm为半径的圆
2、已知⊙O的半径是4,OA=3,则点A与⊙O的位置关系是( )
A.点A在圆内
B.点A在圆上
C.点A在圆外
D.无法确定
3、⊙O的半径为3cm,若点P在⊙O内,则OP的长可能是( )
A.2cm
B.3cm
C.4cm
D.5cm
4、⊙O的半径为5,点A到圆心O的距离为d,已知点A在⊙O的外部,则( )
A.d<5
B.d>5
C.d≥5
D.d=5
5、若⊙O的半径为5,点P到圆心的距离为d,当点P在圆上时,则有(
)
A.d<5
B.d>5
C.d
=
5
D.d
=
6、已知⊙O的半径OA长为1,OB,则可以得到的正确图形可能是( )
A.B.
C.D.
7、若点A在⊙O内,点B在⊙O外,OA=3,OB=5,则⊙O的半径r的取值范围是(
)
A.0<r<3
B.2<r<8
C.3<r<5
D.r>5
8、已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内
B.在⊙O外
C.在⊙O上
D.无法确定
9、已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2﹣2x+d=0有实根,则点P( )
A.在⊙O的内部
B.在⊙O的外部
C.在⊙O上
D.在⊙O上或⊙O的内部
10、如图,在中,,,,点E是中点.以B为圆心,为半径画圆,则点E与的位置关系是(
)
A.点E在内
B.点E在上
C.点E在外
D.无法判断
二、填空题
11、到定点O的距离等于4的点的集合是
.
12、已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A在⊙O (填“上”“外”或“内”)
13、已知⊙O的半径为6cm,当OP=6cm时,点P在
;当OP
时,点P在圆内;当OP
时,点P不在圆外.
14、在平面内,⊙O的半径为2cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .
15、已知圆O的半径为5,P是线段OA的中点,若OA=10,则点P在⊙O ,点A在⊙O .
16、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
,点B在⊙C
.
17、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
.
18、在平面直角坐标系中,以原点O为圆心,5为半径作⊙O,已知A,B,C三点的坐标分别为A(3,4),B(-3,-3),C(4,-),则A,B,C三点与⊙O的位置关系分别为
19、如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最小值为
.
(19题)
(20题)
20、如图,在平面直角坐标系中,已知点,,,点P在以为圆心,1为半径的圆上运动,且始终满足,a的最大值是_________.
三、解答题
21、如图,⊙O'过坐标原点O,点O'的坐标为(1,1).判断点P(﹣1,1),点Q(0,1),点R(2,2)和⊙O'的位置关系.
22、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,那么点导火索的人每秒跑6.5cm是否安全?
23、已知⊙O的半径为2,点P到圆心O的距离OP=m,且m使关于x的方程有实数根,求点P与⊙O的位置关系.
24、如图,已知BD、CE是△ABC的高,M是BC的中点,则点B,C,D,E是否在以点M为圆心的圆上?为什么?
25、在中,AB=3厘米,BC=4厘米,CA=5厘米.
(1)以点A为圆心,以3厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(2)以点A为圆心,以4厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(3)以点B为圆心,以4厘米长为半径画圆,确定点A,C与⊙B的位置关系.
2.1.1圆的概念、点和圆的位置关系
-2021-2022学年苏科版九年级数学上册
培优训练(答案)
一、选择题
1、下列条件能确定圆的是(
)
A.以O为圆心的圆
B.以2
cm为半径的圆
C.经过已知点A的圆
D.以点O为圆心,以1
cm为半径的圆
【答案】D
【解析】解:由圆的概念可知,确定一个圆有两个要素:圆心和半径,两者缺一不可,由此可得:A只有圆心,错误;B只有半径,错误;C经过已知点A的圆,圆心和半径都不确定,错误;D确定了圆心和半径,正确.故选D
.
2、已知⊙O的半径是4,OA=3,则点A与⊙O的位置关系是( )
A.点A在圆内
B.点A在圆上
C.点A在圆外
D.无法确定
【分析】根据⊙O的半径r=4,且点A到圆心O的距离d=3知d<r,据此可得答案.
【解析】∵⊙O的半径r=4,且点A到圆心O的距离d=3,
∴d<r,
∴点A在⊙O内,
故选:A.
3、⊙O的半径为3cm,若点P在⊙O内,则OP的长可能是( )
A.2cm
B.3cm
C.4cm
D.5cm
【分析】根据点在圆内,点到圆心的距离小于圆的半径进行判断.
【解答】解⊙O的半径为3cm,点P在⊙O内,
∴OP<3cm.
故选:A.
4、⊙O的半径为5,点A到圆心O的距离为d,已知点A在⊙O的外部,则( )
A.d<5
B.d>5
C.d≥5
D.d=5
【分析】根据点与圆的位置关系判断得出即可.
【解析】∵点A在圆O的外部,圆O的半径为5,
∴点A到圆心O的距离d的范围是:d>5.
故选:B.
5、若⊙O的半径为5,点P到圆心的距离为d,当点P在圆上时,则有(
)
A.d<5
B.d>5
C.d
=
5
D.d
=
【答案】C由于点P在圆上,所以点P到圆心的距离等于圆的半径,即d=5.故选:C.
6、已知⊙O的半径OA长为1,OB,则可以得到的正确图形可能是( )
A.B.
C.D.
【分析】根据点到圆心的距离和圆的半径的大小关系判断点与圆的位置关系即可.
【解析】∵⊙O的半径OA长1,若OB,
∴OA<OB,∴点B在圆外,
故选:D.
7、若点A在⊙O内,点B在⊙O外,OA=3,OB=5,则⊙O的半径r的取值范围是(
)
A.0<r<3
B.2<r<8
C.3<r<5
D.r>5
【答案】C
【解析】解:∵点A在半径为r的⊙O内,点B在⊙O外,
∴OA小于r,OB大于r,
∵OA=3,OB=5,∴3<r<5.故选:C.
8、已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内
B.在⊙O外
C.在⊙O上
D.无法确定
【分析】关于x的方程x2﹣2dx+1=0有两个相等的实数根,即判别式△=b2﹣4ac=0.即可得到关于d的不等式,从而求得d的范围,进而判断点A与⊙O的位置关系.
【解析】∵a=1,b=﹣2d,c=1,
∴△=b2﹣4ac=(﹣2d)2﹣4×1×1=4d2﹣4=0,
解得:d=1.
则点A在⊙O上.
故选:C.
9、已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2﹣2x+d=0有实根,则点P( )
A.在⊙O的内部
B.在⊙O的外部
C.在⊙O上
D.在⊙O上或⊙O的内部
【分析】首先根据关于x的方程有实数根求得d的取值范围,然后利用d与半径的大小关系判断点与圆的位置关系.
【解析】∵关于x的方程x2﹣2x+d=0有实根,∴根的判别式△=(﹣2)2﹣4×d≥0,解得d≤1,
∴点在圆内或在圆上,
故选:D.
10、如图,在中,,,,点E是中点.以B为圆心,为半径画圆,则点E与的位置关系是(
)
A.点E在内
B.点E在上
C.点E在外
D.无法判断
【答案】A
【解析】解:在Rt△ABC中,∠C=90°,AC=4,BC=3,
由勾股定理得到:
∵E为AB的中点,∴BE=AB=2.5.
∵BC=3,∴BE<BC,∴点E在⊙B的内部,故选:A.
二、填空题
11、到定点O的距离等于4的点的集合是
.
【答案】以定点O为圆心,4为半径的圆
12、已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A在⊙O (填“上”“外”或“内”)
【解答】解:∵OA=3cm<4cm∴点A在⊙O内.
故答案是:内.
13、已知⊙O的半径为6cm,当OP=6cm时,点P在
;当OP
时,点P在圆内;当OP
时,点P不在圆外.
【答案】圆上;<6cm;≤6cm
14、在平面内,⊙O的半径为2cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .
【解答】解:∵⊙O的半径为2cm,点P到圆心O的距离为3cm,
∴d>r,
∴点P与⊙O的位置关系是:P在⊙O外.
故答案为:点P在圆外
15、已知圆O的半径为5,P是线段OA的中点,若OA=10,则点P在⊙O ,点A在⊙O .
【解答】解:∵P为OA的中点,
∴OP=OA=5,
∴OP=r=5,
∴点P在⊙O上;
∵OA=10>r,
∴点A在圆外.
故答案为上,外;
16、在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,
则点A在⊙C
,点B在⊙C
.
【答案】上;外
17、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
.
【答案】3
【答案】点A在⊙O上,点B在⊙O内,点C在⊙O外
19、如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最小值为
.
【分析】作AB的中点E,连接EM、CE,根据直角三角形斜边上的中线等于斜边的一半以及三角形的中位线定理求得CE和EM的长,然后确定CM的范围.
【解析】作AB的中点E,连接EM、CE.
在直角△ABC中,
∵E是直角△ABC斜边AB上的中点,∴CE=AB=2.5.
∵M是BD的中点,E是AB的中点,∴ME=AD=1.
∵2.5﹣1≤CM≤2.5+1,即1.5≤CM≤3.5.∴最小值为1.5,
故答案为:1.5.
20、如图,在平面直角坐标系中,已知点,,,点P在以为圆心,1为半径的圆上运动,且始终满足,a的最大值是_________.
【答案】1+.
【解析】解:连接PA,
∵A(2,0),B(2?a,0),C(2+a,0),
∴AB=AC=a,
∵∠BPC=90°,∴PA=AB=AC=a,
∵DA=,
∴点P为直线AD与圆的交点重合时,a取最大和最小值,即:a的最大值=1+.
故答案为:1+.
三、解答题
21、如图,⊙O'过坐标原点O,点O'的坐标为(1,1).判断点P(﹣1,1),点Q(0,1),点R(2,2)和⊙O'的位置关系.
【解答】解:圆的半径是,
PO′=2>,则P在⊙O′的外部;
QO′=1<,则Q在⊙O′的内部;
RO′==圆的半径,故R在圆上.
22、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,已知这个导火索的长度为18cm,那么点导火索的人每秒跑6.5cm是否安全?
解:点导火索的人安全。
导火索燃烧的时间为:,
此时点导火索的人跑的路程为
因为130>120,所以点导火索的人安全。
23、已知⊙O的半径为2,点P到圆心O的距离OP=m,且m使关于x的方程有实数根,求点P与⊙O的位置关系.
【答案】点P在圆上或圆内
解:=,
,即
∴点P在圆上或圆内
24、如图,已知BD、CE是△ABC的高,M是BC的中点,则点B,C,D,E是否在以点M为圆心的圆上?为什么?
解:点B,C,D,E在以点M为圆心的圆上
连接ME,MD,
∵RtBEC、RtBDC中,M是BC的中点,
,
∴点B,C,D,E在以点M为圆心的圆上
25、在中,AB=3厘米,BC=4厘米,CA=5厘米.
(1)以点A为圆心,以3厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(2)以点A为圆心,以4厘米长为半径画圆,确定点B,C与⊙A的位置关系;
(3)以点B为圆心,以4厘米长为半径画圆,确定点A,C与⊙B的位置关系.
解:如图,以点A为圆心,以3厘米长为半径画圆,点B在上,点C在外.
如图,以点A为圆心,以4厘米长为半径画圆,点B在内,C在外.
如图,以点B为圆心,以4厘米长为半径画圆,点A在内,C与上.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
