第4章一元一次方程——用一元一次方程解决其它问题专题练习2021-2022学年苏科版七年级上册数学(Word版 含答案)
文档属性
| 名称 | 第4章一元一次方程——用一元一次方程解决其它问题专题练习2021-2022学年苏科版七年级上册数学(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 16:34:52 | ||
图片预览



文档简介
苏科版七年级上册数学第4章一元一次方程
用一元一次方程解决实际问题其它问题专题练习
填空题:
1.日历中成一竖列的连续三个日期的和是33,这三天分别是
号,
号,
号.
2.我市计划把某一段公路的一侧全部栽上丁香树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔7米栽1棵,则树苗缺17棵;如果每隔8米栽1棵,则树苗多出1棵.原有树苗
棵.
3.自来水公司为鼓励节约用水,对水费按以下方式收取:用水不超过10吨,每吨按2元收费,超过10吨的部分按每吨3元收费,王老师三月份平均水费为每吨2.5元收费,则王老师家三月份用水
吨.
4.某同学把积攒的零用钱1000元存入银行,月利率是0.24%,如果到期他连本带利可取回1024元,那么他共存了
个月.
5.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/小时,水速为2千米/时,则A港和B港相距
千米.
6.如果一个两位数上的十位数是个位数的一半,两个数位上的数字之和为9,则这个两位数是
.
7.如图为一块在电脑屏幕上出现的色块图,由6个颜色不同的正方形拼成的长方形,如果中间最小的正方形边长为1,则所拼成的长方形的面积是
.
二、选择题:
1.一个长方形的周长为30cm,若这个长方形的长减少1cm,宽增加2cm就可成为一个正方形,设长方形的长为xcm,可列方程为( )
A.x+1=(15﹣x)﹣2
B.x+1=(30﹣x)﹣2
C.x﹣1=(15﹣x)+2
D.x﹣1=(30﹣x)+2
2.“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是( )
A.3x+1=4x﹣2
B.3x﹣1=4x+2
C.
D.
3.中国古代问题:有甲、乙两个牧童,甲对乙说:“把你的羊给我一只,我的羊数就是你的羊数的2倍”.乙回答说:“最好还是把你的羊给我一只,我们羊数就一样了”.若设甲有x只羊,则下列方程正确的是( )
A.x+1=2(x﹣2)
B.x+3=2(x﹣1)
C.x+1=2(x﹣3)
D.
4.一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有50m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40m2墙面,每名一级技工比二级技工一天多粉刷10m2墙面,设每个房间需要粉刷的墙面面积为xm2,则下列的方程正确的是( )
A.
B.
C.+10
D.+10
5.今年父亲的年龄是儿子年龄的3倍,6年前父亲的年龄是儿子年龄的4倍.设今年儿子的年龄为x岁,则下列式子正确的是( )
A.4x﹣6=3(x﹣6)
B.4x+6=3(x+6)
C.3x+6=4(x+6)
D.3x﹣6=4(x﹣6)
6.一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.0.8(1+0.5)x=x+28
B.0.8(1+0.5)x=x﹣28
C.0.8(1+0.5x)=x﹣28
D.0.8(1+0.5x)=x+28
7.今年哥哥的年龄是妹妹年龄的2倍,4年前哥哥的年龄是妹妹年龄的3倍,若设妹妹今年x岁,可列方程为( )
A.2x﹣4=3(x﹣4)
B.2x=3(x﹣4)
C.2x+4=3(x﹣4)
D.2x+4=3x
8.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )
A.3(x+4)=4(x+1)
B.3x+4=4x+1
C.3(x﹣4)=4(x﹣1)
D.
9.在一个笼子里面放着几只鸡与几只兔,数了数一共有14个头,44只脚.问鸡兔各有几只设鸡为x只,得方程( )
A.2x+4(14﹣x)=44
B.4x+2(14﹣x)=44
C.4x+2(x﹣14)=44
D.2x+4(x﹣14)=44
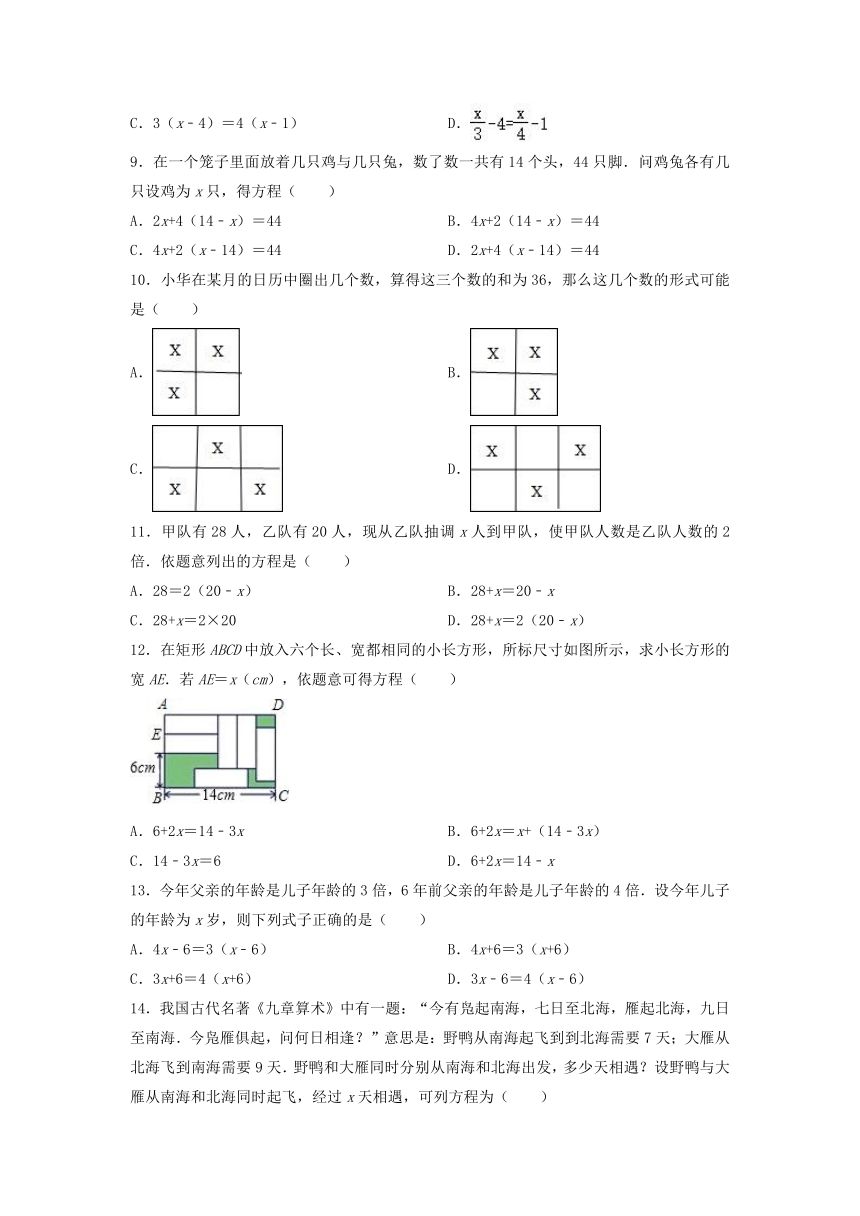
10.小华在某月的日历中圈出几个数,算得这三个数的和为36,那么这几个数的形式可能是( )
A.
B.
C.
D.
11.甲队有28人,乙队有20人,现从乙队抽调x人到甲队,使甲队人数是乙队人数的2倍.依题意列出的方程是( )
A.28=2(20﹣x)
B.28+x=20﹣x
C.28+x=2×20
D.28+x=2(20﹣x)
12.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x
B.6+2x=x+(14﹣3x)
C.14﹣3x=6
D.6+2x=14﹣x
13.今年父亲的年龄是儿子年龄的3倍,6年前父亲的年龄是儿子年龄的4倍.设今年儿子的年龄为x岁,则下列式子正确的是( )
A.4x﹣6=3(x﹣6)
B.4x+6=3(x+6)
C.3x+6=4(x+6)
D.3x﹣6=4(x﹣6)
14.我国古代名著《九章算术》中有一题:“今有凫起南海,七日至北海,雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞到到北海需要7天;大雁从北海飞到南海需要9天.野鸭和大雁同时分别从南海和北海出发,多少天相遇?设野鸭与大雁从南海和北海同时起飞,经过x天相遇,可列方程为( )
A.9x﹣7x=1
B.9x+7x+1
C.x+x=1
D.x﹣x=1
解答题:
一个三位数,百位上的数字比十位上的数字大1,个位上的数字比十位上的数字的3倍少2,若将个位与百位数字调换位置后,所得的三位数与原三位数的和是1171,求这个三位数.
2、如图3-4-1,周长为68的长方形ABCD被分成7个大小完全一样的长方形,求长方形ABCD的面积.
3、李伟从家里骑摩托车到火车站,若每小时行30千米,则比火车开车时间早到15分钟;若每小时行18千米,则比火车开车时间迟到15分钟.现在李伟打算在火车开车前10分钟到达火车站,求李伟此时骑摩托车的速度应该是多少?
4、某足球联赛—个赛季共进行26轮比赛(即每队均需参赛26场),其中胜—场得3分,平一场得1分,负一场得0分.某队在这个赛季中平的场数比负的场数多7场,结果得34分,则这个队在这一赛季中胜、平、负的场数分别是多少?
5.如图1,线段AB=60厘米.
(1)点P沿线段AB自A点向B点以4厘米/分的速度运动,同时点Q沿直线自B点向A点以6厘米/分的速度运动,几分钟后,P、Q两点相遇?
(2)几分钟后,P、Q两点相距20厘米?
(3)如图2,AO=PO=8厘米,∠POB=40°,现将点P绕着点O以20度/分的速度顺时针旋转一周后停止,同时点Q沿直线BA沿B点向A点运动,假若P、Q两点也能相遇,求点Q的速度.
6.整理一批图书,由一个人做要40小时完成,现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?
参考答案
填空题:
1.解:设最小的日期为x,则其他两个日期分别为x+7,x+14,
依题意,得:x+x+7+x+14=33,
解得:x=4,
∴x+7=11,x+14=18.
故答案为:4;11;18.
2.解:设英语兴趣小组有x人,
x(1+)=30,
解得,x=25
答:英语兴趣小组有25人,
故答案为:25.
3.解:设王老师家三月份用水x吨,
依题意,得:10×2+(x﹣10)×3=2.5x,
解得:x=20.
故答案为:20.
4.解:设他共存了x个月,
依题意,得:1000+1000×0.24%x=1024,
解得:x=10.
故答案为:10.
5.解:设A港和B港相距x千米.
根据题意,得,
解之得x=504.
故填504.
6.解:设个位上的数为a,则十位上的数为
由题意得:a=9,
解得:a=6,
=3,
所以,这个两位数是36.
7.解:设第二小的正方形的边长为x,
则有:x+x+(x+1)=(x+2)+(x+3),
解得:x=4,
所以长方形的长为13,宽为11,面积=13×11=143.
故答案是:143.
选择题:
1.解:∵长方形的周长为30cm,长方形的长为xcm,
则长方形的宽为(15﹣x)cm,
根据题意,得:x﹣1=15﹣x+2,
故选:C.
2.解:∵设共有x个苹果,
∴每个小朋友分3个则剩1个时,小朋友的人数是:,
若每个小朋友分4个则少2个时,小朋友的人数是:,
∴,
故选:C.
3.解:∵甲对乙说:“把你的羊给我1只,我的羊数就是你的羊数的两倍”.甲有x只羊,
∴乙有+1只,
∵乙回答说:“最好还是把你的羊给我1只,我们的羊数就一样了”,
∴+1+1=x﹣1,即x+1=2(x﹣3)
故选:C.
4.解:设每个房间需要粉刷的墙面面积为xm2,
根据题意,得=+10.
故选:D.
5.解:由题意可得,3x﹣6=4(x﹣6),
故选:D.
6.解:设这件夹克衫的成本价是x元,
由题意得,0.8(1+50%)x﹣x=28,
即0.8(1+0.5)x=28+x.
故选:A.
7.解:设妹妹今年x岁.
2x﹣4=3(x﹣4).
故选:A.
8.解:根据将绳三折测之,绳多四尺,则绳长为:3(x+4),根据绳四折测之,绳多一尺,则绳长为:4(x+1),
故3(x+4)=4(x+1).
故选:A.
9.解:设鸡为x只,则要鸡有2x只脚,兔有4(14﹣x)只脚,
根据等量关系列方程为
2x+4(14﹣x)=44,
故选:A.
10.解:第一个图中:设下面的数是x,则上面的数是x﹣7,右边的是x﹣6.根据题意得:x+(x﹣7)+(x﹣6)=36,解得x=不合题意.
第二图中:设下面的数是x,则上面的数是x﹣7,左边的数是x﹣8.根据题意得:x+(x﹣7)+(x﹣8)=36,解得x=17,符合题意.可能是这种形式.
第三图中:设下面左边的数是x,则右边的数是:x+2,上面的数是x+1﹣7=x﹣6,根据题意得:x+(x+2)+(x﹣6)=36解得:x=,不合题意.
第四图中:设下面左边的数是x,则上边左边的是:x﹣7﹣1=x﹣8右边的数是:x﹣7+1=x﹣6根据题意得:x+(x﹣8)+(x﹣6)=36解得:x=,不合题意.
故选:B.
11.解:设从乙队抽调x人到甲队,则现在甲队人数是(28+x)人,乙队人数是(20﹣x)人,根据等量关系列方程得:28+x=2(20﹣x),
故选:D.
12.解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
13.解:由题意可得,3x﹣6=4(x﹣6),
故选:D.
20.解:由题意可得,
,
故选:C.
解答题:
1、解:设原三位数的十位上的数字是x,
则百位上的数字是x+1,个位上的数字是3x-2.
根据题意,得100(x+1)+10x+(3x-2)+100(3x-2)+10x+x+1=1171,
解得x=3.
x+1=3+1=4≠0,3x-2=3×3-2=7≠0.
所以原三位数是100×(3+1)+10×3+(3×3-2)=437.
答:原三位数是437.
2、解:设小长方形的宽为x,则大长方形长为5x,小
长方形长为2.
5x,因此大长方形宽为x+2.
5x.由长方形周长公式得2(5x+x+2.
5x)=68,
解得x=4.
所以长方形ABCD的面积是5×4×(4+2.5×4)=280.
答:长方形ABCD的面积是280.
3、解:设李伟家到火车站的路程为x千米,则由开车时间固定这一等量关系,
可简便得出方程:.
解得x=.
李伟从家出发到火车开车时间为(小时).
李伟应有的速度为
=27(千米/时)
答:李伟此时骑摩托车的速度为27千米/时.
4、解:设该队负的场数是x场,则平了(x+7)场,胜了(26-x-x-7)场.
根据题意得:3(26-x-x-7)+x+7=34
解得:x=6
则平了x+7=13,
胜了26-x-x-7=7,
答:这个队在这一赛季胜、平、负的场数分别是7,13,6场.
5、解:(1)设经过x分钟后,P、Q两点相遇,依题意得:
4x+6x=60,解得:x=6.
答:经过6分钟后,P、Q两点相遇.
(2)设经过y分钟后,P、Q两点相距20厘米,依题意得:
①4y+6y+20=60,解得:y=4;
②4y+6y﹣20=60,解得:y=8.
答:经过4或8分钟后,P、Q两点相距20厘米.
(3)由题意知,点P、Q只能在直线AB上相遇,则点P旋转到直线上的时间为2分钟或11分钟.
设点Q的速度为t厘米/分,依题意得:
①2t=60﹣16,解得:t=22;
②11t=60,解得:t=.
答:点Q的速度为22厘米/分或厘米/分.
6、解:设具体应先安排x人工作,
根据题意得:+=1,
即:x+2(x+2)=10,
解得:x=2.
答:具体应先安排2人工作.
用一元一次方程解决实际问题其它问题专题练习
填空题:
1.日历中成一竖列的连续三个日期的和是33,这三天分别是
号,
号,
号.
2.我市计划把某一段公路的一侧全部栽上丁香树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔7米栽1棵,则树苗缺17棵;如果每隔8米栽1棵,则树苗多出1棵.原有树苗
棵.
3.自来水公司为鼓励节约用水,对水费按以下方式收取:用水不超过10吨,每吨按2元收费,超过10吨的部分按每吨3元收费,王老师三月份平均水费为每吨2.5元收费,则王老师家三月份用水
吨.
4.某同学把积攒的零用钱1000元存入银行,月利率是0.24%,如果到期他连本带利可取回1024元,那么他共存了
个月.
5.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/小时,水速为2千米/时,则A港和B港相距
千米.
6.如果一个两位数上的十位数是个位数的一半,两个数位上的数字之和为9,则这个两位数是
.
7.如图为一块在电脑屏幕上出现的色块图,由6个颜色不同的正方形拼成的长方形,如果中间最小的正方形边长为1,则所拼成的长方形的面积是
.
二、选择题:
1.一个长方形的周长为30cm,若这个长方形的长减少1cm,宽增加2cm就可成为一个正方形,设长方形的长为xcm,可列方程为( )
A.x+1=(15﹣x)﹣2
B.x+1=(30﹣x)﹣2
C.x﹣1=(15﹣x)+2
D.x﹣1=(30﹣x)+2
2.“某幼儿园给小朋友分苹果,若每个小朋友分3个则剩1个;若每个小朋友分4个则少2个,问苹果有多少个?”若设共有x个苹果,则列出的方程是( )
A.3x+1=4x﹣2
B.3x﹣1=4x+2
C.
D.
3.中国古代问题:有甲、乙两个牧童,甲对乙说:“把你的羊给我一只,我的羊数就是你的羊数的2倍”.乙回答说:“最好还是把你的羊给我一只,我们羊数就一样了”.若设甲有x只羊,则下列方程正确的是( )
A.x+1=2(x﹣2)
B.x+3=2(x﹣1)
C.x+1=2(x﹣3)
D.
4.一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有50m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40m2墙面,每名一级技工比二级技工一天多粉刷10m2墙面,设每个房间需要粉刷的墙面面积为xm2,则下列的方程正确的是( )
A.
B.
C.+10
D.+10
5.今年父亲的年龄是儿子年龄的3倍,6年前父亲的年龄是儿子年龄的4倍.设今年儿子的年龄为x岁,则下列式子正确的是( )
A.4x﹣6=3(x﹣6)
B.4x+6=3(x+6)
C.3x+6=4(x+6)
D.3x﹣6=4(x﹣6)
6.一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.0.8(1+0.5)x=x+28
B.0.8(1+0.5)x=x﹣28
C.0.8(1+0.5x)=x﹣28
D.0.8(1+0.5x)=x+28
7.今年哥哥的年龄是妹妹年龄的2倍,4年前哥哥的年龄是妹妹年龄的3倍,若设妹妹今年x岁,可列方程为( )
A.2x﹣4=3(x﹣4)
B.2x=3(x﹣4)
C.2x+4=3(x﹣4)
D.2x+4=3x
8.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )
A.3(x+4)=4(x+1)
B.3x+4=4x+1
C.3(x﹣4)=4(x﹣1)
D.
9.在一个笼子里面放着几只鸡与几只兔,数了数一共有14个头,44只脚.问鸡兔各有几只设鸡为x只,得方程( )
A.2x+4(14﹣x)=44
B.4x+2(14﹣x)=44
C.4x+2(x﹣14)=44
D.2x+4(x﹣14)=44
10.小华在某月的日历中圈出几个数,算得这三个数的和为36,那么这几个数的形式可能是( )
A.
B.
C.
D.
11.甲队有28人,乙队有20人,现从乙队抽调x人到甲队,使甲队人数是乙队人数的2倍.依题意列出的方程是( )
A.28=2(20﹣x)
B.28+x=20﹣x
C.28+x=2×20
D.28+x=2(20﹣x)
12.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x
B.6+2x=x+(14﹣3x)
C.14﹣3x=6
D.6+2x=14﹣x
13.今年父亲的年龄是儿子年龄的3倍,6年前父亲的年龄是儿子年龄的4倍.设今年儿子的年龄为x岁,则下列式子正确的是( )
A.4x﹣6=3(x﹣6)
B.4x+6=3(x+6)
C.3x+6=4(x+6)
D.3x﹣6=4(x﹣6)
14.我国古代名著《九章算术》中有一题:“今有凫起南海,七日至北海,雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞到到北海需要7天;大雁从北海飞到南海需要9天.野鸭和大雁同时分别从南海和北海出发,多少天相遇?设野鸭与大雁从南海和北海同时起飞,经过x天相遇,可列方程为( )
A.9x﹣7x=1
B.9x+7x+1
C.x+x=1
D.x﹣x=1
解答题:
一个三位数,百位上的数字比十位上的数字大1,个位上的数字比十位上的数字的3倍少2,若将个位与百位数字调换位置后,所得的三位数与原三位数的和是1171,求这个三位数.
2、如图3-4-1,周长为68的长方形ABCD被分成7个大小完全一样的长方形,求长方形ABCD的面积.
3、李伟从家里骑摩托车到火车站,若每小时行30千米,则比火车开车时间早到15分钟;若每小时行18千米,则比火车开车时间迟到15分钟.现在李伟打算在火车开车前10分钟到达火车站,求李伟此时骑摩托车的速度应该是多少?
4、某足球联赛—个赛季共进行26轮比赛(即每队均需参赛26场),其中胜—场得3分,平一场得1分,负一场得0分.某队在这个赛季中平的场数比负的场数多7场,结果得34分,则这个队在这一赛季中胜、平、负的场数分别是多少?
5.如图1,线段AB=60厘米.
(1)点P沿线段AB自A点向B点以4厘米/分的速度运动,同时点Q沿直线自B点向A点以6厘米/分的速度运动,几分钟后,P、Q两点相遇?
(2)几分钟后,P、Q两点相距20厘米?
(3)如图2,AO=PO=8厘米,∠POB=40°,现将点P绕着点O以20度/分的速度顺时针旋转一周后停止,同时点Q沿直线BA沿B点向A点运动,假若P、Q两点也能相遇,求点Q的速度.
6.整理一批图书,由一个人做要40小时完成,现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?
参考答案
填空题:
1.解:设最小的日期为x,则其他两个日期分别为x+7,x+14,
依题意,得:x+x+7+x+14=33,
解得:x=4,
∴x+7=11,x+14=18.
故答案为:4;11;18.
2.解:设英语兴趣小组有x人,
x(1+)=30,
解得,x=25
答:英语兴趣小组有25人,
故答案为:25.
3.解:设王老师家三月份用水x吨,
依题意,得:10×2+(x﹣10)×3=2.5x,
解得:x=20.
故答案为:20.
4.解:设他共存了x个月,
依题意,得:1000+1000×0.24%x=1024,
解得:x=10.
故答案为:10.
5.解:设A港和B港相距x千米.
根据题意,得,
解之得x=504.
故填504.
6.解:设个位上的数为a,则十位上的数为
由题意得:a=9,
解得:a=6,
=3,
所以,这个两位数是36.
7.解:设第二小的正方形的边长为x,
则有:x+x+(x+1)=(x+2)+(x+3),
解得:x=4,
所以长方形的长为13,宽为11,面积=13×11=143.
故答案是:143.
选择题:
1.解:∵长方形的周长为30cm,长方形的长为xcm,
则长方形的宽为(15﹣x)cm,
根据题意,得:x﹣1=15﹣x+2,
故选:C.
2.解:∵设共有x个苹果,
∴每个小朋友分3个则剩1个时,小朋友的人数是:,
若每个小朋友分4个则少2个时,小朋友的人数是:,
∴,
故选:C.
3.解:∵甲对乙说:“把你的羊给我1只,我的羊数就是你的羊数的两倍”.甲有x只羊,
∴乙有+1只,
∵乙回答说:“最好还是把你的羊给我1只,我们的羊数就一样了”,
∴+1+1=x﹣1,即x+1=2(x﹣3)
故选:C.
4.解:设每个房间需要粉刷的墙面面积为xm2,
根据题意,得=+10.
故选:D.
5.解:由题意可得,3x﹣6=4(x﹣6),
故选:D.
6.解:设这件夹克衫的成本价是x元,
由题意得,0.8(1+50%)x﹣x=28,
即0.8(1+0.5)x=28+x.
故选:A.
7.解:设妹妹今年x岁.
2x﹣4=3(x﹣4).
故选:A.
8.解:根据将绳三折测之,绳多四尺,则绳长为:3(x+4),根据绳四折测之,绳多一尺,则绳长为:4(x+1),
故3(x+4)=4(x+1).
故选:A.
9.解:设鸡为x只,则要鸡有2x只脚,兔有4(14﹣x)只脚,
根据等量关系列方程为
2x+4(14﹣x)=44,
故选:A.
10.解:第一个图中:设下面的数是x,则上面的数是x﹣7,右边的是x﹣6.根据题意得:x+(x﹣7)+(x﹣6)=36,解得x=不合题意.
第二图中:设下面的数是x,则上面的数是x﹣7,左边的数是x﹣8.根据题意得:x+(x﹣7)+(x﹣8)=36,解得x=17,符合题意.可能是这种形式.
第三图中:设下面左边的数是x,则右边的数是:x+2,上面的数是x+1﹣7=x﹣6,根据题意得:x+(x+2)+(x﹣6)=36解得:x=,不合题意.
第四图中:设下面左边的数是x,则上边左边的是:x﹣7﹣1=x﹣8右边的数是:x﹣7+1=x﹣6根据题意得:x+(x﹣8)+(x﹣6)=36解得:x=,不合题意.
故选:B.
11.解:设从乙队抽调x人到甲队,则现在甲队人数是(28+x)人,乙队人数是(20﹣x)人,根据等量关系列方程得:28+x=2(20﹣x),
故选:D.
12.解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
13.解:由题意可得,3x﹣6=4(x﹣6),
故选:D.
20.解:由题意可得,
,
故选:C.
解答题:
1、解:设原三位数的十位上的数字是x,
则百位上的数字是x+1,个位上的数字是3x-2.
根据题意,得100(x+1)+10x+(3x-2)+100(3x-2)+10x+x+1=1171,
解得x=3.
x+1=3+1=4≠0,3x-2=3×3-2=7≠0.
所以原三位数是100×(3+1)+10×3+(3×3-2)=437.
答:原三位数是437.
2、解:设小长方形的宽为x,则大长方形长为5x,小
长方形长为2.
5x,因此大长方形宽为x+2.
5x.由长方形周长公式得2(5x+x+2.
5x)=68,
解得x=4.
所以长方形ABCD的面积是5×4×(4+2.5×4)=280.
答:长方形ABCD的面积是280.
3、解:设李伟家到火车站的路程为x千米,则由开车时间固定这一等量关系,
可简便得出方程:.
解得x=.
李伟从家出发到火车开车时间为(小时).
李伟应有的速度为
=27(千米/时)
答:李伟此时骑摩托车的速度为27千米/时.
4、解:设该队负的场数是x场,则平了(x+7)场,胜了(26-x-x-7)场.
根据题意得:3(26-x-x-7)+x+7=34
解得:x=6
则平了x+7=13,
胜了26-x-x-7=7,
答:这个队在这一赛季胜、平、负的场数分别是7,13,6场.
5、解:(1)设经过x分钟后,P、Q两点相遇,依题意得:
4x+6x=60,解得:x=6.
答:经过6分钟后,P、Q两点相遇.
(2)设经过y分钟后,P、Q两点相距20厘米,依题意得:
①4y+6y+20=60,解得:y=4;
②4y+6y﹣20=60,解得:y=8.
答:经过4或8分钟后,P、Q两点相距20厘米.
(3)由题意知,点P、Q只能在直线AB上相遇,则点P旋转到直线上的时间为2分钟或11分钟.
设点Q的速度为t厘米/分,依题意得:
①2t=60﹣16,解得:t=22;
②11t=60,解得:t=.
答:点Q的速度为22厘米/分或厘米/分.
6、解:设具体应先安排x人工作,
根据题意得:+=1,
即:x+2(x+2)=10,
解得:x=2.
答:具体应先安排2人工作.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
