2021-2022学年人教版数学八年级上册13.2画轴对称图形课件(19张ppt)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.2画轴对称图形课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 288.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第十三章
轴对称
13.2
画轴对称图形
第1课时
画轴对称图形
情景导入
如图,给出了一个图案的一半,其中的虚线是这个图案的对称轴.(1)你能猜出整个图案的形状吗?(2)你能画出这个图案的另一半吗?
想一想
几何图形都可以看作是由点组成的,我们只要分别作出这些点关于对称轴的对应点,再连接这些对应点便可以得到原图形的轴对称图形.
如何作出点A,B,C,D关于直线l的对称点呢?
合作探究
知识板块一 轴对称变换
在一张半透明纸张的左边部分,画出左脚印,如何由此得到相应的右脚印?
请动手在一张纸上画一个你喜欢的图形,将这张纸
纸折叠,描图,再打开纸,看看你得到了什么?
由一个平面图形得到与它关于一条直线对称的图形.
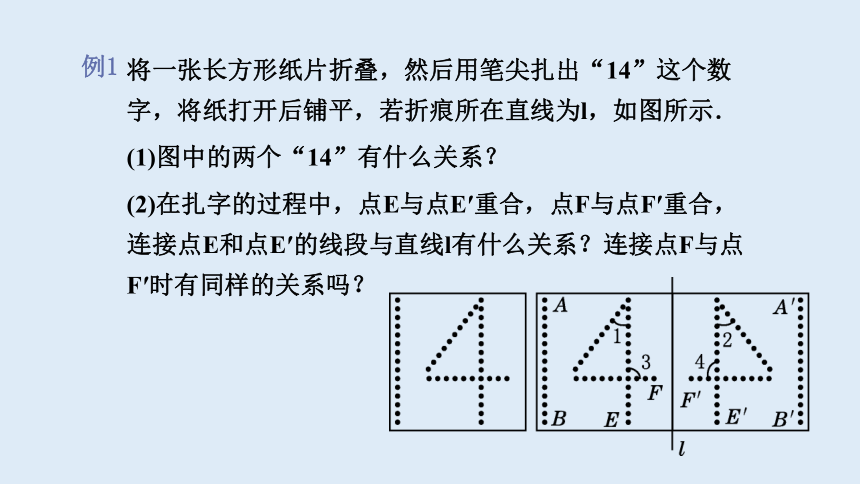
将一张长方形纸片折叠,然后用笔尖扎出“14”这个数字,将纸打开后铺平,若折痕所在直线为l,如图所示.
(1)图中的两个“14”有什么关系?
(2)在扎字的过程中,点E与点E′重合,点F与点F′重合,连接点E和点E′的线段与直线l有什么关系?连接点F与点F′时有同样的关系吗?
例1
分析:依题意可知,两个“14”是关于直线l对称的图形,由轴对称的性质不难解决本题.
解:(1)图中的两个“14”是以直线l为对称轴的轴对称
图形.
(2)EE′被直线l垂直平分,FF′也被直线l垂直平分.
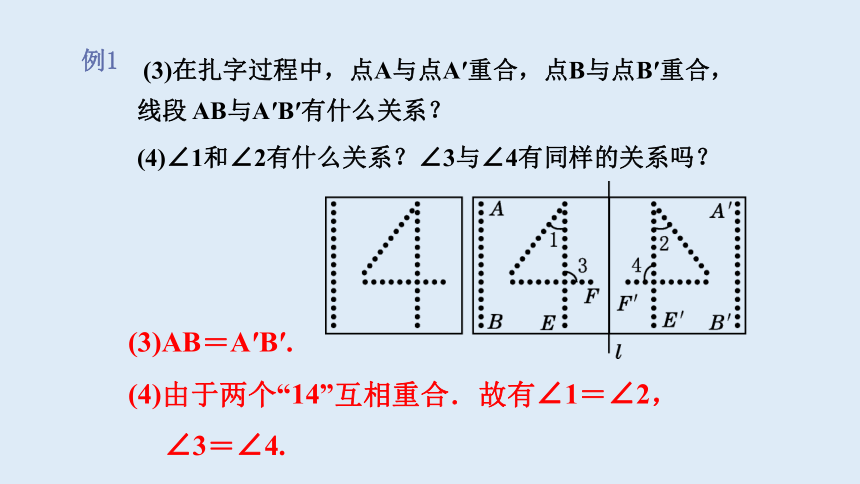
(3)在扎字过程中,点A与点A′重合,点B与点B′重合,线段
AB与A′B′有什么关系?
(4)∠1和∠2有什么关系?∠3与∠4有同样的关系吗?
例1
(3)AB=A′B′.
(4)由于两个“14”互相重合.故有∠1=∠2,
∠3=∠4.
轴对称变换的性质:
轴对称变换前后两个图形的形状、大小一样,说明它们全等;即:变换前后的对应线段相等,对应角相等.
合作探究
知识板块二
画轴对称图形或成轴对称
如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称
的图形呢?
1.
依据:如果一个图形关于某一条直线对称,那么
连接任意一对对称点的线段被对称轴垂直平分.
2.画轴对称图形的步骤:
画轴对称图形要经历一找二作三连这三个步骤:
(1)找:在原图形上找特殊点(如线段的端点);
(2)作:作各个特殊点关于对称轴的对称点;
(3)连:按原图的顺序连接所作的各对称点.
3.画出的新图形与原图形的关系:
(1)新图形与原图形的形状、大小完全相同;
(2)新图形上的每一点都是原图形上的某一点关于对称轴的对称点;
(3)连接任意一对对应点的线段被对称轴垂直平分.
如图,已知△ABC和直线l,画出与关于直线
l
对称的图形.
分析:
△ABC可以由三个顶点的位置确定,只要能分别画
出这三个顶点
关于直线l的对称点,连接这些对称点,就能得到要画的图形.
A
B
C
l
例2
画法:(1)
如图,过点A画直线l
的垂线,垂
足为O,在垂线上截取
OA'
=
OA,A'就是点A
关于直线
l
的对称点;
(2)
同理,分别画出点B,C
关于直线
l
的
对称点B',C';
(3)
连接
A'B',
B'C',C'A',则
△
A'B'C'
即为所求.
画好后,你也可以通过折叠的方法验证一下
A
B
C
l
A′
O
B′
C′
几何图形都可以看作由点组成.对于某些图形,只要画出图形中的一
些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形
的轴对称图形.
1.如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形
如“
”的图形,将纸片展开,得到的图形是( )
当堂演练
D
当堂演练
解:如图,分别作出点B,C关于直线l的对称点B′,C′,再依次连接AB′,B′C′,C′A,则△AB′C′即为所求.
2.已知:如图,已知△ABC,过点A作直线l.
求作:△A′B′C′,使它与△ABC关于直线l对称.
当堂演练
3.如图,将矩形纸片ABCD沿对角线BD折叠,使点C落在点C′处,BC′交AD于点E.
(1)若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有多少个?
(2)图中有全等三角形吗?如果有,请写出图中一对全等的三角形,并说明理由;如果没有,也请说明理由.
解:(1)5个;
(2)有,△BCD≌△BC′D,△ABE≌△C′DE,理由略.
课堂总结
作轴对称图形的方法:
(1)确定原图形的关键点;
(2)作出每个关键点关于对称轴对称的对称点;
(3)按原图形的顺序依次连接相应的对称点.
第十三章
轴对称
13.2
画轴对称图形
第1课时
画轴对称图形
情景导入
如图,给出了一个图案的一半,其中的虚线是这个图案的对称轴.(1)你能猜出整个图案的形状吗?(2)你能画出这个图案的另一半吗?
想一想
几何图形都可以看作是由点组成的,我们只要分别作出这些点关于对称轴的对应点,再连接这些对应点便可以得到原图形的轴对称图形.
如何作出点A,B,C,D关于直线l的对称点呢?
合作探究
知识板块一 轴对称变换
在一张半透明纸张的左边部分,画出左脚印,如何由此得到相应的右脚印?
请动手在一张纸上画一个你喜欢的图形,将这张纸
纸折叠,描图,再打开纸,看看你得到了什么?
由一个平面图形得到与它关于一条直线对称的图形.
将一张长方形纸片折叠,然后用笔尖扎出“14”这个数字,将纸打开后铺平,若折痕所在直线为l,如图所示.
(1)图中的两个“14”有什么关系?
(2)在扎字的过程中,点E与点E′重合,点F与点F′重合,连接点E和点E′的线段与直线l有什么关系?连接点F与点F′时有同样的关系吗?
例1
分析:依题意可知,两个“14”是关于直线l对称的图形,由轴对称的性质不难解决本题.
解:(1)图中的两个“14”是以直线l为对称轴的轴对称
图形.
(2)EE′被直线l垂直平分,FF′也被直线l垂直平分.
(3)在扎字过程中,点A与点A′重合,点B与点B′重合,线段
AB与A′B′有什么关系?
(4)∠1和∠2有什么关系?∠3与∠4有同样的关系吗?
例1
(3)AB=A′B′.
(4)由于两个“14”互相重合.故有∠1=∠2,
∠3=∠4.
轴对称变换的性质:
轴对称变换前后两个图形的形状、大小一样,说明它们全等;即:变换前后的对应线段相等,对应角相等.
合作探究
知识板块二
画轴对称图形或成轴对称
如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称
的图形呢?
1.
依据:如果一个图形关于某一条直线对称,那么
连接任意一对对称点的线段被对称轴垂直平分.
2.画轴对称图形的步骤:
画轴对称图形要经历一找二作三连这三个步骤:
(1)找:在原图形上找特殊点(如线段的端点);
(2)作:作各个特殊点关于对称轴的对称点;
(3)连:按原图的顺序连接所作的各对称点.
3.画出的新图形与原图形的关系:
(1)新图形与原图形的形状、大小完全相同;
(2)新图形上的每一点都是原图形上的某一点关于对称轴的对称点;
(3)连接任意一对对应点的线段被对称轴垂直平分.
如图,已知△ABC和直线l,画出与关于直线
l
对称的图形.
分析:
△ABC可以由三个顶点的位置确定,只要能分别画
出这三个顶点
关于直线l的对称点,连接这些对称点,就能得到要画的图形.
A
B
C
l
例2
画法:(1)
如图,过点A画直线l
的垂线,垂
足为O,在垂线上截取
OA'
=
OA,A'就是点A
关于直线
l
的对称点;
(2)
同理,分别画出点B,C
关于直线
l
的
对称点B',C';
(3)
连接
A'B',
B'C',C'A',则
△
A'B'C'
即为所求.
画好后,你也可以通过折叠的方法验证一下
A
B
C
l
A′
O
B′
C′
几何图形都可以看作由点组成.对于某些图形,只要画出图形中的一
些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形
的轴对称图形.
1.如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形
如“
”的图形,将纸片展开,得到的图形是( )
当堂演练
D
当堂演练
解:如图,分别作出点B,C关于直线l的对称点B′,C′,再依次连接AB′,B′C′,C′A,则△AB′C′即为所求.
2.已知:如图,已知△ABC,过点A作直线l.
求作:△A′B′C′,使它与△ABC关于直线l对称.
当堂演练
3.如图,将矩形纸片ABCD沿对角线BD折叠,使点C落在点C′处,BC′交AD于点E.
(1)若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有多少个?
(2)图中有全等三角形吗?如果有,请写出图中一对全等的三角形,并说明理由;如果没有,也请说明理由.
解:(1)5个;
(2)有,△BCD≌△BC′D,△ABE≌△C′DE,理由略.
课堂总结
作轴对称图形的方法:
(1)确定原图形的关键点;
(2)作出每个关键点关于对称轴对称的对称点;
(3)按原图形的顺序依次连接相应的对称点.
