2021-2022学年人教版数学七年级上册1.4.1.1有理数的乘法课件(27张ppt)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册1.4.1.1有理数的乘法课件(27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 18:36:52 | ||
图片预览




文档简介
(共27张PPT)
1.4
有理数的乘除法
1.4.1
有理数的乘法
第1课时
解:5×3
=
15
计算:
5×3
×
0×
解:0×
=
0
解:
×
=
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
本节学习目标
1.掌握有理数乘法法则,
3.能够运用有理数的乘法法则进行有关计算.
2.初步了解有理数乘法法则的合理性.
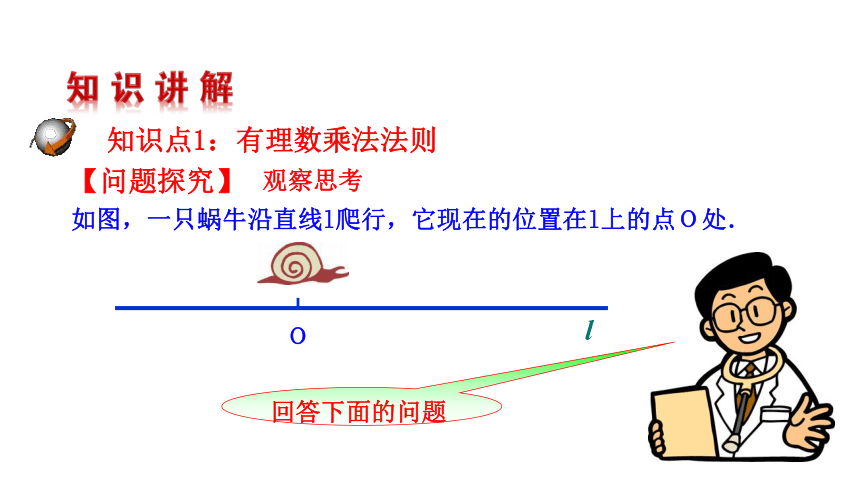
知识点1:有理数乘法法则
【问题探究】
观察思考
回答下面的问题
如图,一只蜗牛沿直线l爬行,它现在的位置在l上的点O处.
l
O
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?
规定:向左为负,向右为正.现在之前为负,现在之后为正.
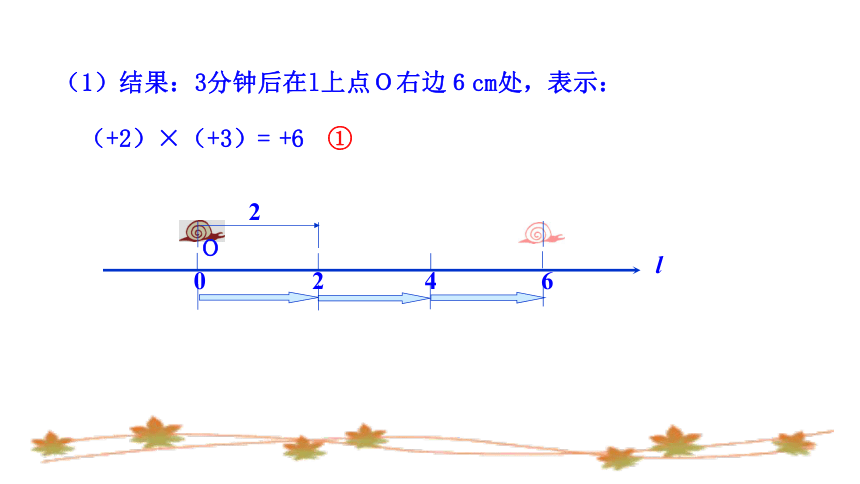
(1)结果:3分钟后在l上点O右边6cm处,表示:
(+2)×(+3)=
①
2
0
2
6
4
l
O
+6
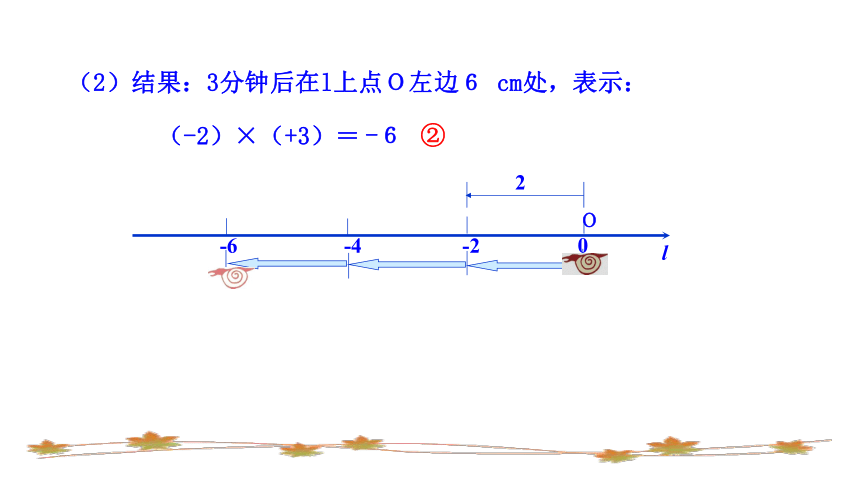
(2)结果:3分钟后在l上点O左边6
cm处,表示:
(-2)×(+3)=
②
-6
-4
0
-2
2
l
O
-6
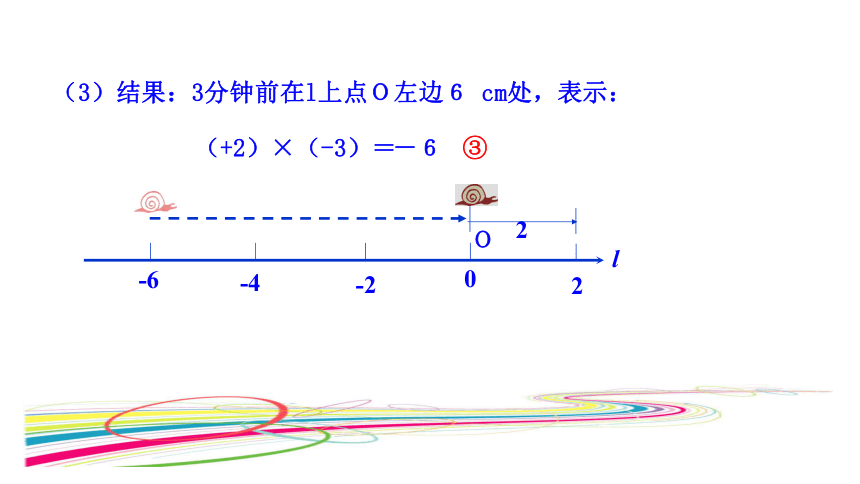
(+2)×(-3)=
2
-6
-4
0
-2
2
(3)结果:3分钟前在l上点O左边6
cm处,表示:
l
-6
O
③
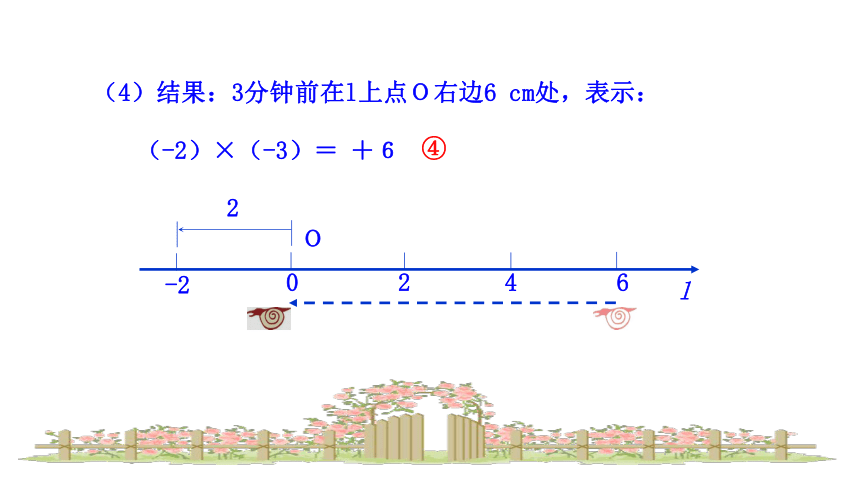
(4)结果:3分钟前在l上点O右边6
cm处,表示:
(-2)×(-3)=
2
0
2
6
4
-2
+6
l
O
④
正
正
负
负
积
观察①~④式,根据你对有理数乘法的思考,
填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数.
乘积的绝对值等于各乘数绝对值的___.
综合如下:
(1)
2×3=6
(2)(-2)×3=-6
(3)
2×(-3)=-6
(4)(-2)×(-3)=6
(5)
被乘数或乘数为0时,结果是0
同号得正
异号得负
异号得负
同号得正
有什么规律?
归纳总结:
有理数乘法法则:两数相乘,同号得正,异号得负,并且把绝对值相乘.任何数与0相乘,都得0.
认真记呦!
【跟踪训练】
-
-
+
+
1.确定下列积的符号:
(1)5×(-3)
(2)(-4)×6
(3)(-7)×(-9)
(4)0.5×0.7
(1)(-5)×(-4).
(2)(
)×
.
(3)2
×(-3.5).
(4)(-0.57)×
0.
解:(1)(-5)×(-4)
=5×4=20.
(3)2×(-3.5)=
-(2
×
3.5)=
-7.
(4)(-0.57)×0=0.
注意:有理数相乘,先确定积的符号,再确定积的值.一个数同1相乘仍得这个数,一个数同-1相乘得这个数的相反数.
(2)
2.计算:
例1
计算:
(1)
9×6
;
(2)
(?9)×6
;
(3)
3
×
(-4)
=
12;
(3)
3
×(-4);
(4)(-3)×(-4).
=
?(3
×4)
=
?
12;
【例题讲解】
解:(1)
9×6
=
+(9×6)
=54
;
求解步骤:
1、确定积的符号
2、绝对值相乘
(2)
(?9)×6
=
?(9×6)
=
?
54;
(4)(-3)
×
(-4)
=
+(3×4)
【跟踪训练】
计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6)
×0=
(5)
×(- )=
(6)(- )
×
=
-54
-24
6
0
知识点2:互为倒数
【问题探究】
计算:
归纳:若两个有理数的乘积为1,就称这两个有理数互为倒数(0没有倒数).
(1)
;
(2)(
-3)×(
-
).
解:(1)原式=
=1.
(2)原式=
+(3×
)=1.
请你写出下列各数的倒数:
(1)-1
,(2)-2
,(3)
,(4)-
.
练一练
解:请你写出下列各数的倒数:
(1)-1
的倒数是-1.
(2)-2
的倒数是-
.
(3)
的倒数是
.
(4)-
的倒数是-
.
【例题讲解】
例
2
用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3
km后,气温有什么变化?
解:(-6)×3=
-18.
答:气温下降18
℃.
【跟踪训练】
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:(-5)X60=-300,即销售额减少300元
关于倒数的几点提醒
知识拓展:
【举一反三】
a、b是两个有理数,若ab<0,且a+b>0,则下列结论正确的是( )
A.a>0,b>0
B.a、b两数异号,且正数的绝对值大
C.a<0,b<0
D.a、b两数异号,且负数的绝对值大
乘法运算中符号的确定
B
解:因为ab<0,所以a、b异号,又因为a+b>0,
所以正数的绝对值较大.
倒数的应用
【思考交流】
成功属于我!
若a、b互为相反数,c、d互为倒数,m的绝对值为2.
(1)直接写出a+b,cd,m的值;
(2)求m+cd+
的值.
解:(1)因为a、b互为相反数,c、d互为倒数,
m的绝对值为2,所以a+b=0,cd=1,m=±2.
(2)当m=2时,m+cd+
=2+1+0=3;
当m=-2时,m+cd+
=-2+1+0=-1.
【迁移应用】
有理数乘法中的分类讨论
(2021?金昌期末)已知|x|=3,|y|=2,且xy<0,则x-y的值等于( )
A.-1或1
B.5或-5
C.5或-1
D.-5或1
解:因为|x|=3,|y|=2,所以x=±3,y=±2,
因为xy<0,所以x=3,y=-2或x=-3,y=2,
所以x-y=5或-5.
B
敞开心扉说一说
先确定积的符号,再把绝对值相乘,当有一个因数为0时,积为0.
2.如何进行两个有理数的运算:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并且把绝对值相乘.
任何数与0相乘,都得0.
A
试试就能行
1.(2020?安顺中考)计算(-3)×2的结果是( )
A.-6
B.-1
C.1
D.6
2.如果□
,则“□”内应填的实数是(
)
A.
B.
C.
D.
D
3.(2020?泰安中考)?
的倒数是( )
A.-2
B.-
C.2
D.
A
4.若ab<0,则a,b必定满足( )
A.a>0,b<0
B.a<0,b>0
C.a>0,b<0或a<0,b>0
D.无法确定
C
5.规定:水位上升为正,水位下降为负;几天后为正,几天前为负.若水位每天下降4cm,今天的水位记为0cm,那么3天前的水位是多少米?
解:由题意,得(-4)×(-3)=12(cm).
即3天前的水位是12cm.
1.4
有理数的乘除法
1.4.1
有理数的乘法
第1课时
解:5×3
=
15
计算:
5×3
×
0×
解:0×
=
0
解:
×
=
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
本节学习目标
1.掌握有理数乘法法则,
3.能够运用有理数的乘法法则进行有关计算.
2.初步了解有理数乘法法则的合理性.
知识点1:有理数乘法法则
【问题探究】
观察思考
回答下面的问题
如图,一只蜗牛沿直线l爬行,它现在的位置在l上的点O处.
l
O
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?
规定:向左为负,向右为正.现在之前为负,现在之后为正.
(1)结果:3分钟后在l上点O右边6cm处,表示:
(+2)×(+3)=
①
2
0
2
6
4
l
O
+6
(2)结果:3分钟后在l上点O左边6
cm处,表示:
(-2)×(+3)=
②
-6
-4
0
-2
2
l
O
-6
(+2)×(-3)=
2
-6
-4
0
-2
2
(3)结果:3分钟前在l上点O左边6
cm处,表示:
l
-6
O
③
(4)结果:3分钟前在l上点O右边6
cm处,表示:
(-2)×(-3)=
2
0
2
6
4
-2
+6
l
O
④
正
正
负
负
积
观察①~④式,根据你对有理数乘法的思考,
填空:
正数乘正数积为___数;
负数乘正数积为___数;
正数乘负数积为___数;
负数乘负数积为___数.
乘积的绝对值等于各乘数绝对值的___.
综合如下:
(1)
2×3=6
(2)(-2)×3=-6
(3)
2×(-3)=-6
(4)(-2)×(-3)=6
(5)
被乘数或乘数为0时,结果是0
同号得正
异号得负
异号得负
同号得正
有什么规律?
归纳总结:
有理数乘法法则:两数相乘,同号得正,异号得负,并且把绝对值相乘.任何数与0相乘,都得0.
认真记呦!
【跟踪训练】
-
-
+
+
1.确定下列积的符号:
(1)5×(-3)
(2)(-4)×6
(3)(-7)×(-9)
(4)0.5×0.7
(1)(-5)×(-4).
(2)(
)×
.
(3)2
×(-3.5).
(4)(-0.57)×
0.
解:(1)(-5)×(-4)
=5×4=20.
(3)2×(-3.5)=
-(2
×
3.5)=
-7.
(4)(-0.57)×0=0.
注意:有理数相乘,先确定积的符号,再确定积的值.一个数同1相乘仍得这个数,一个数同-1相乘得这个数的相反数.
(2)
2.计算:
例1
计算:
(1)
9×6
;
(2)
(?9)×6
;
(3)
3
×
(-4)
=
12;
(3)
3
×(-4);
(4)(-3)×(-4).
=
?(3
×4)
=
?
12;
【例题讲解】
解:(1)
9×6
=
+(9×6)
=54
;
求解步骤:
1、确定积的符号
2、绝对值相乘
(2)
(?9)×6
=
?(9×6)
=
?
54;
(4)(-3)
×
(-4)
=
+(3×4)
【跟踪训练】
计算(口答):
(1)6×(-9)=
(2)(-4)×6=
(3)(-6)×(-1)=
(4)(-6)
×0=
(5)
×(- )=
(6)(- )
×
=
-54
-24
6
0
知识点2:互为倒数
【问题探究】
计算:
归纳:若两个有理数的乘积为1,就称这两个有理数互为倒数(0没有倒数).
(1)
;
(2)(
-3)×(
-
).
解:(1)原式=
=1.
(2)原式=
+(3×
)=1.
请你写出下列各数的倒数:
(1)-1
,(2)-2
,(3)
,(4)-
.
练一练
解:请你写出下列各数的倒数:
(1)-1
的倒数是-1.
(2)-2
的倒数是-
.
(3)
的倒数是
.
(4)-
的倒数是-
.
【例题讲解】
例
2
用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km的变化量为-6℃,攀登3
km后,气温有什么变化?
解:(-6)×3=
-18.
答:气温下降18
℃.
【跟踪训练】
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:(-5)X60=-300,即销售额减少300元
关于倒数的几点提醒
知识拓展:
【举一反三】
a、b是两个有理数,若ab<0,且a+b>0,则下列结论正确的是( )
A.a>0,b>0
B.a、b两数异号,且正数的绝对值大
C.a<0,b<0
D.a、b两数异号,且负数的绝对值大
乘法运算中符号的确定
B
解:因为ab<0,所以a、b异号,又因为a+b>0,
所以正数的绝对值较大.
倒数的应用
【思考交流】
成功属于我!
若a、b互为相反数,c、d互为倒数,m的绝对值为2.
(1)直接写出a+b,cd,m的值;
(2)求m+cd+
的值.
解:(1)因为a、b互为相反数,c、d互为倒数,
m的绝对值为2,所以a+b=0,cd=1,m=±2.
(2)当m=2时,m+cd+
=2+1+0=3;
当m=-2时,m+cd+
=-2+1+0=-1.
【迁移应用】
有理数乘法中的分类讨论
(2021?金昌期末)已知|x|=3,|y|=2,且xy<0,则x-y的值等于( )
A.-1或1
B.5或-5
C.5或-1
D.-5或1
解:因为|x|=3,|y|=2,所以x=±3,y=±2,
因为xy<0,所以x=3,y=-2或x=-3,y=2,
所以x-y=5或-5.
B
敞开心扉说一说
先确定积的符号,再把绝对值相乘,当有一个因数为0时,积为0.
2.如何进行两个有理数的运算:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并且把绝对值相乘.
任何数与0相乘,都得0.
A
试试就能行
1.(2020?安顺中考)计算(-3)×2的结果是( )
A.-6
B.-1
C.1
D.6
2.如果□
,则“□”内应填的实数是(
)
A.
B.
C.
D.
D
3.(2020?泰安中考)?
的倒数是( )
A.-2
B.-
C.2
D.
A
4.若ab<0,则a,b必定满足( )
A.a>0,b<0
B.a<0,b>0
C.a>0,b<0或a<0,b>0
D.无法确定
C
5.规定:水位上升为正,水位下降为负;几天后为正,几天前为负.若水位每天下降4cm,今天的水位记为0cm,那么3天前的水位是多少米?
解:由题意,得(-4)×(-3)=12(cm).
即3天前的水位是12cm.
