2.6.3 有理数的加减混合运算(3) 课件(共26张PPT)
文档属性
| 名称 | 2.6.3 有理数的加减混合运算(3) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 16:20:31 | ||
图片预览






文档简介
(共26张PPT)
2.6.3有理数的加减混合运算(3)
第二章
有理数及其运算
2021-2022学年七年级数学上册同步(北师版)
1.熟悉在水位变化过程中出现的量,进一步加深对有理数意义的理解,巩固用有理数表示实际生活中的量.
2.能综合运用有理数及其加法减法的有关知识,解决简单的实际问题,从中体会数学与现实生活的联系.
3.能用折线统计图描述实例的变化过程.
学习目标
有理数加减混合运算的步骤
(1)把算式中的减法都转化为加法;
(2)省略加号与括号;
(3)进行运算(尽可能利用运算律简化计算).
新课导入
加减混合运算的应用
右图是流花河的水文资料(单位:m),取河流的警戒水位作为
0
点,那么图中的其他数据可以分别记作什么?
35.3
33.4
22.6
11.5
流花河水位
最高水位
警戒水位
平均水位
最低水位
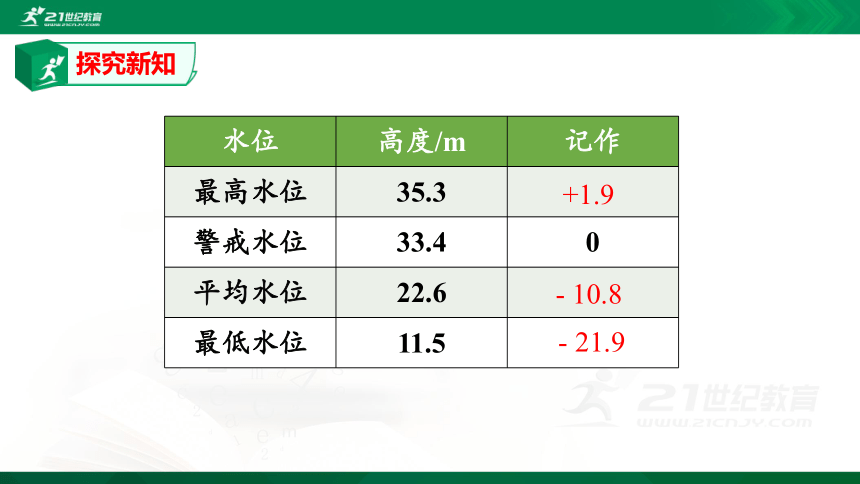
探究新知
水位
高度/m
记作
最高水位
35.3
警戒水位
33.4
0
平均水位
22.6
最低水位
11.5
+1.9
-
10.8
-
21.9
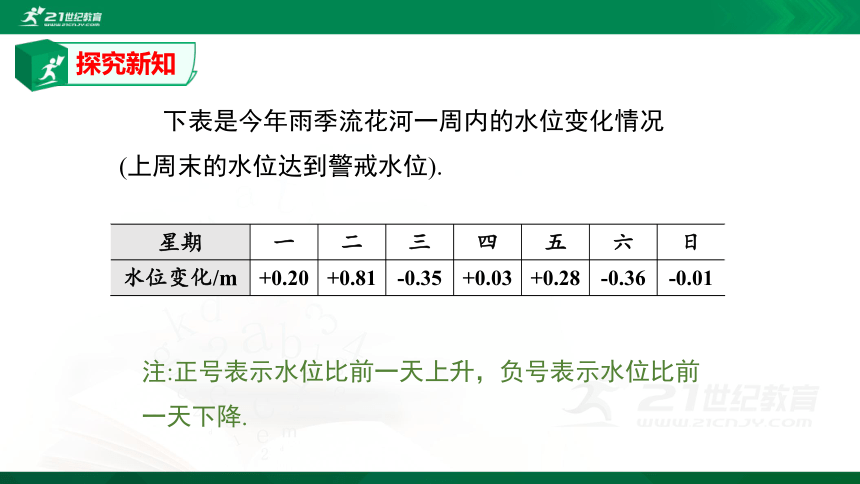
探究新知
下表是今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位).
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
探究新知
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
周二水位最高,在警戒线之上.
距离警戒线:
0.20+0.81=1.01(m)
探究新知
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
周一水位最低,在警戒线之上.
距离警戒线:
0.20
m.
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
探究新知
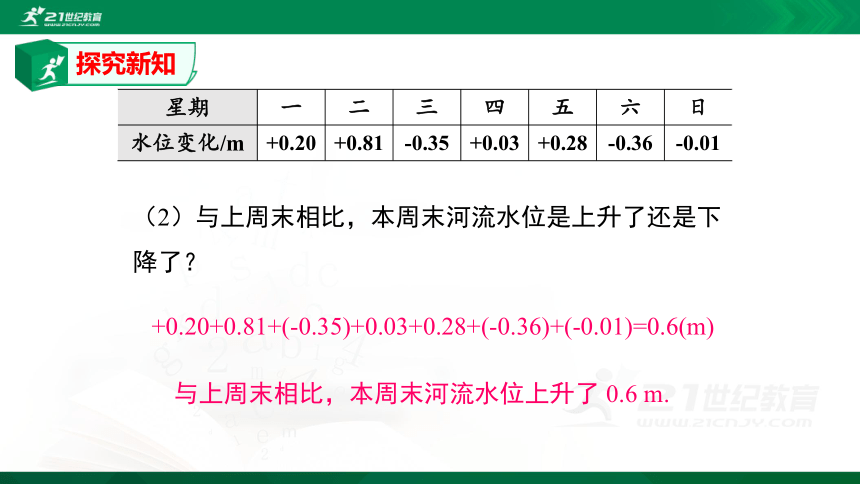
(2)与上周末相比,本周末河流水位是上升了还是下降了?
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
与上周末相比,本周末河流水位上升了
0.6
m.
+0.20+0.81+(-0.35)+0.03+0.28+(-0.36)+(-0.01)=0.6(m)
探究新知
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
(3)完成下面的本周水位记录表:
星期
一
二
三
四
五
六
日
水位记录/m
33.6
34.41
34.06
34.09
34.37
34.01
34
探究新知
(4)以警戒水位为
0
点,用折线统计图表示本周的水位变化情况.
0
0.2
0.4
0.6
0.8
1.0
探究新知
例.
某气象员为了掌握一周内天气的变化情况,测量了一周内的气温.
下表是一周内气温变化情况(用正数表示比前一日上升的度数,用负数表示下降的度数)
试分析经过一周,气温是上升还是下降了.
解:2+(-1)+(-2)+4+(-2.5)+1+0.5=2(℃).
答:经过一周气温上升了2
℃.
星期
一
二
三
四
五
六
日
气温变化/℃
2
-1
-2
4
-2.5
1
0.5
例题讲解
例.
已知上周周五(周末不开盘)收盘时股市指数以2880点报收,本周内股市涨跌情况如下表,则本周四收盘时的股市指数是多少?
解:正数表示涨,负数表示跌,每天的变化是相对于前一天来比较的,所以周四的股市指数为2880+50-21-100+78=2887.
星期
一
二
三
四
五
股指变化
+50
-21
-100
+78
-78
例题讲解
1.
一天早晨的气温是-7
℃,中午上升了11
℃,晚上又下降9
℃,则晚上的气温是(
)
A.
-5
℃
B.
-6
℃
C.
-7
℃
D.
-8
℃
A
2.
某天上午6:00虹桥水库的水位为30.4
m,到上午11:30分水位上涨了5.3
m,则下午6:00的水位下跌了0.9
m.
则下午6:00的水位为(
)
A.
26
m
B.
34.8
m
C.
35.8
m
D.
36.6
m
B
课堂练习
3.
一个人在南北方向的路上行走,如果规定向北为正,这个人走了+25
m,接着走了-10
m,又走了-20
m,那么他实际上(
)
A.
向北走了5
m
B.
向南走了10
m
C.
向南走了5
m
D.
向北走了10
m
C
4.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测试的成绩是(
)
A.90分
B.75分
C.91分
D.81分
C
5.
一个病人每天下午需要测量血压,该病人上周日的收缩压为120单位,下表是该病人这周一到周五与前一天相比较收缩压的变化情况:
本周星期二的收缩压是(
)
A.
110
B.
120
C.
125
D.
130
A
星期
一
二
三
四
五
增减
+20
-30
-25
+15
+30
6.
去年7月份小明到银行开户,存入1500元,以后每月根据收支情况存入一笔钱,下表为小明从
8月份到12月份的存款情况:
则截止到去年12月份,存折上共有(
)
A.
9
750元
B.
8
050元
C.
1
750元
D.
9
550元
D
月份
8
9
10
11
12
与上一月比较
-100
-200
+500
+300
-250
7.
南京出租车司机小李某一时段全是在中山东路上来回行驶,你能否知道在他将最后一位乘客送到目的地时,他距离出车的出发点有多远?
解:该出租车离出发点的距离为:
15+(-2)+5+(-1)+(-10)+(
-3)+(
-2)+12+4+(
-5)
=13千米
答:他距离出车的出发点13千米
如果规定向东为正,向西为负,我行车里程(单位:千米)为:
15,
-2,
5,
-1,
-10,
-3,
-2,
12,
4,
-5,
8.某摩托车厂本周(周一至周五)内计划每日生产300
辆摩托车.由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划生产量相比情况如下表.
(增加的车辆数记为正数,减少的车辆数记为负数)
星期
一
二
三
四
五
实际与计划相比/辆
-50
-72
+35
+42
+10
(1)本周三生产了
辆摩托车;
(2)本周总生产量与计划生产量相比,是增加了还是减少了?
(3)产量最多的一天比产量最少的一天多生产了多少辆车?
(3)
42-(-72)=114(辆).
所以产量最多的一天比产量最少的一天多生产114辆车.
.
(2)
(-50)+(-72)+(+35)+(+42)+(+10)=-50-72+35+42+10
=-35.
所以本周产量比计划减少了35辆.
.
解:(1)
本周三生产了300+35=335(辆)
.
9.
一位病人每天下午需要测量一次血压,下表是该病人星期一至星期五收缩压的变化情况.该病人上个星期日的收缩压为
160
单位.
(1)请算出星期五该病人的收缩压;
(2)请用折线统计图表示该病人这
5
天的收缩压情况.
30
–
20
+
17
+
18
–
20
=
30
+
17
+
18
–
20
–
20
=
25
(单位)
解:(1)
160
+
25
=
185(单位)
答:星期五该病人的收缩压为
185
单位.
160
170
180
190
200
日
一
二
三
四
五
星期
收缩压
有理数加减混合运算的应用
会用数学去解决生活中的变化现象,对于几次连续的变化情况可以用有理数的加减法去解决
借助表格折线统计图形象直观地反映事物的变化情况
.
很多实际问题可以转化为有理数的加减混合运算来解决,根据需要可以“人为”地规定零点.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
2.6.3有理数的加减混合运算(3)
第二章
有理数及其运算
2021-2022学年七年级数学上册同步(北师版)
1.熟悉在水位变化过程中出现的量,进一步加深对有理数意义的理解,巩固用有理数表示实际生活中的量.
2.能综合运用有理数及其加法减法的有关知识,解决简单的实际问题,从中体会数学与现实生活的联系.
3.能用折线统计图描述实例的变化过程.
学习目标
有理数加减混合运算的步骤
(1)把算式中的减法都转化为加法;
(2)省略加号与括号;
(3)进行运算(尽可能利用运算律简化计算).
新课导入
加减混合运算的应用
右图是流花河的水文资料(单位:m),取河流的警戒水位作为
0
点,那么图中的其他数据可以分别记作什么?
35.3
33.4
22.6
11.5
流花河水位
最高水位
警戒水位
平均水位
最低水位
探究新知
水位
高度/m
记作
最高水位
35.3
警戒水位
33.4
0
平均水位
22.6
最低水位
11.5
+1.9
-
10.8
-
21.9
探究新知
下表是今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位).
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
探究新知
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
周二水位最高,在警戒线之上.
距离警戒线:
0.20+0.81=1.01(m)
探究新知
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
周一水位最低,在警戒线之上.
距离警戒线:
0.20
m.
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
探究新知
(2)与上周末相比,本周末河流水位是上升了还是下降了?
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
与上周末相比,本周末河流水位上升了
0.6
m.
+0.20+0.81+(-0.35)+0.03+0.28+(-0.36)+(-0.01)=0.6(m)
探究新知
星期
一
二
三
四
五
六
日
水位变化/m
+0.20
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
(3)完成下面的本周水位记录表:
星期
一
二
三
四
五
六
日
水位记录/m
33.6
34.41
34.06
34.09
34.37
34.01
34
探究新知
(4)以警戒水位为
0
点,用折线统计图表示本周的水位变化情况.
0
0.2
0.4
0.6
0.8
1.0
探究新知
例.
某气象员为了掌握一周内天气的变化情况,测量了一周内的气温.
下表是一周内气温变化情况(用正数表示比前一日上升的度数,用负数表示下降的度数)
试分析经过一周,气温是上升还是下降了.
解:2+(-1)+(-2)+4+(-2.5)+1+0.5=2(℃).
答:经过一周气温上升了2
℃.
星期
一
二
三
四
五
六
日
气温变化/℃
2
-1
-2
4
-2.5
1
0.5
例题讲解
例.
已知上周周五(周末不开盘)收盘时股市指数以2880点报收,本周内股市涨跌情况如下表,则本周四收盘时的股市指数是多少?
解:正数表示涨,负数表示跌,每天的变化是相对于前一天来比较的,所以周四的股市指数为2880+50-21-100+78=2887.
星期
一
二
三
四
五
股指变化
+50
-21
-100
+78
-78
例题讲解
1.
一天早晨的气温是-7
℃,中午上升了11
℃,晚上又下降9
℃,则晚上的气温是(
)
A.
-5
℃
B.
-6
℃
C.
-7
℃
D.
-8
℃
A
2.
某天上午6:00虹桥水库的水位为30.4
m,到上午11:30分水位上涨了5.3
m,则下午6:00的水位下跌了0.9
m.
则下午6:00的水位为(
)
A.
26
m
B.
34.8
m
C.
35.8
m
D.
36.6
m
B
课堂练习
3.
一个人在南北方向的路上行走,如果规定向北为正,这个人走了+25
m,接着走了-10
m,又走了-20
m,那么他实际上(
)
A.
向北走了5
m
B.
向南走了10
m
C.
向南走了5
m
D.
向北走了10
m
C
4.小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测试的成绩是(
)
A.90分
B.75分
C.91分
D.81分
C
5.
一个病人每天下午需要测量血压,该病人上周日的收缩压为120单位,下表是该病人这周一到周五与前一天相比较收缩压的变化情况:
本周星期二的收缩压是(
)
A.
110
B.
120
C.
125
D.
130
A
星期
一
二
三
四
五
增减
+20
-30
-25
+15
+30
6.
去年7月份小明到银行开户,存入1500元,以后每月根据收支情况存入一笔钱,下表为小明从
8月份到12月份的存款情况:
则截止到去年12月份,存折上共有(
)
A.
9
750元
B.
8
050元
C.
1
750元
D.
9
550元
D
月份
8
9
10
11
12
与上一月比较
-100
-200
+500
+300
-250
7.
南京出租车司机小李某一时段全是在中山东路上来回行驶,你能否知道在他将最后一位乘客送到目的地时,他距离出车的出发点有多远?
解:该出租车离出发点的距离为:
15+(-2)+5+(-1)+(-10)+(
-3)+(
-2)+12+4+(
-5)
=13千米
答:他距离出车的出发点13千米
如果规定向东为正,向西为负,我行车里程(单位:千米)为:
15,
-2,
5,
-1,
-10,
-3,
-2,
12,
4,
-5,
8.某摩托车厂本周(周一至周五)内计划每日生产300
辆摩托车.由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划生产量相比情况如下表.
(增加的车辆数记为正数,减少的车辆数记为负数)
星期
一
二
三
四
五
实际与计划相比/辆
-50
-72
+35
+42
+10
(1)本周三生产了
辆摩托车;
(2)本周总生产量与计划生产量相比,是增加了还是减少了?
(3)产量最多的一天比产量最少的一天多生产了多少辆车?
(3)
42-(-72)=114(辆).
所以产量最多的一天比产量最少的一天多生产114辆车.
.
(2)
(-50)+(-72)+(+35)+(+42)+(+10)=-50-72+35+42+10
=-35.
所以本周产量比计划减少了35辆.
.
解:(1)
本周三生产了300+35=335(辆)
.
9.
一位病人每天下午需要测量一次血压,下表是该病人星期一至星期五收缩压的变化情况.该病人上个星期日的收缩压为
160
单位.
(1)请算出星期五该病人的收缩压;
(2)请用折线统计图表示该病人这
5
天的收缩压情况.
30
–
20
+
17
+
18
–
20
=
30
+
17
+
18
–
20
–
20
=
25
(单位)
解:(1)
160
+
25
=
185(单位)
答:星期五该病人的收缩压为
185
单位.
160
170
180
190
200
日
一
二
三
四
五
星期
收缩压
有理数加减混合运算的应用
会用数学去解决生活中的变化现象,对于几次连续的变化情况可以用有理数的加减法去解决
借助表格折线统计图形象直观地反映事物的变化情况
.
很多实际问题可以转化为有理数的加减混合运算来解决,根据需要可以“人为”地规定零点.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
