2.2.2 平方根(2) 课件(共32张PPT)
文档属性
| 名称 | 2.2.2 平方根(2) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 13:48:54 | ||
图片预览











文档简介
(共32张PPT)
2.2.2
平方根(2)
第二章
实数
2021-2022学年八年级数学上册同步(北师版)
1.了解平方根的概念;掌握平方根的特征。
2.能正确区分平方根与算术平方根的意义。
3.能利用开平方与平方互为逆运算的关系,求某些非负数的平方根。
学习目标
1.算术平方根
定义:若一个正数x的平方等于a,则这个数叫做a的算术平方根。
特别地,0的平方根是0,即
.
2.性质
记作:
,
表示求a的算术平方根
式子
中的双重非负性:
(1)a≥0;
(2)
≥0.
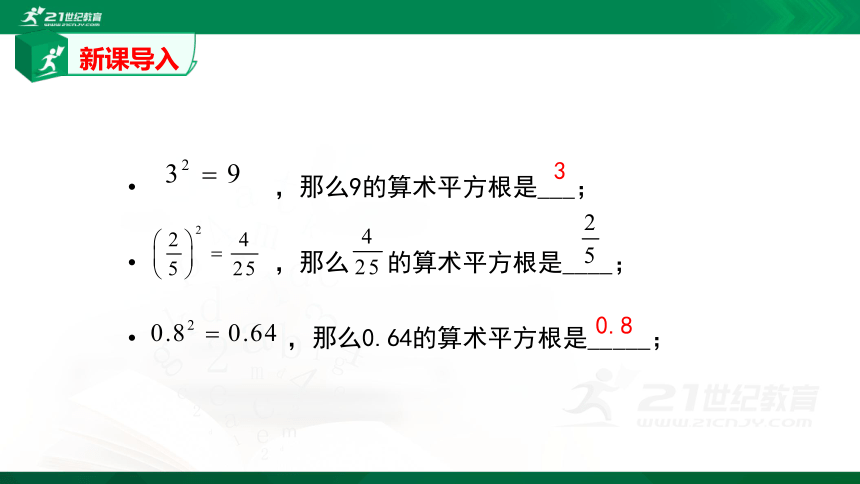
新课导入
,那么9的算术平方根是___;
,那么
的算术平方根是____;
,那么0.64的算术平方根是_____;
3
0.8
新课导入
平方根的概念及性质
问题
9的算术平方根是3,也就是说3的平方是9,还有其他数,它的平方等于9吗?
3和-3有什么特征?
由于(-3)2=9
,所以还有,这个数是-3.因此平方等于9的数有两个,3和-3.
3和-3互为相反数,会不会是巧合呢?
探究新知
(1)
0.8的平方等于0.64,那么0.64的算术平方根就是_____
(2)
的平方等于,那么的算术平方根就是____
(3)
展厅地面为正方形,其面积是49
m2,则其边长为___m.
0.8
7
做一做,想一想
问题
平方等于0.64,,49的数还有吗?
探究新知
(
)2
=
(
)2
=
(
)2
=
(
)2
=
(
)2
=
9
0.64
9
(
)?
=
0.64
3
-3
0.8
-0.8
(
)2
=
(
)2
=
(
)2
=
±3
±0.8
9
0.64
填一填
探究新知
一般地,如果一个数x的平方等于a,即x2=
a,那么这个数叫做a
的平方根(也叫二次方根).
记作:
读作:正负根号a
.
平方根
例:
∵
(±5)2=25
∴
5是25的算术平方根,即
±
=
±5
(
2可以省略)
概念学习
1.
144的平方根是什么?
2.
0的平方根是什么?
3.
的平方根是什么?
4.
-4有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
针对练习
通过这些题目的解答,你能发现什么?
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
想一想
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
只有非负数才有平方根
(算术平方根)
一个正数a的两个平方根互为相反数
正平方根:
负平方根:
平方根的性质:
归纳总结
平方根
算术平方根
联
系
区
别
平方根与算术平方根的联系与区别
一个正数有两个平方根,其中正平方根就是算术平方根
包含关系
相同性
只有非负数才有平方根和算术平方根
0的平方根和算术平方根都是0.
表示方法不同
个数不同
正数有两个平方根
正数只有一个算术平方根
归纳总结
开平方及相关运算
+1
-1
+2
-2
+3
-3
1
4
9
平方
已知一个数,求它的平方的运算,叫作平方运算.
探究新知
+1
-1
+2
-2
+3
-3
1
4
9
?运算
反之,已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
探究新知
开平方与平方是什么关系?
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
已知底数和指数求幂
已知幂和指数求底数
开平方运算
平方运算
归纳总结
开平方与平方的对比
正数与零
任何数
幂
平方根
开
方
平
方
运算符号
适用范围
运算结果名称
性
质
正数有
个平方根,它们是
,
零的平方根是
,
负数
.
正数的平方是
数;
零的平方是
;
负数的平方是
数.
正
正
0
2
0
没有平方根
互为相反数
归纳总结
例1
求下列各数的平方根:
(1)64
;
(2)
(4)
(5)
11.
(3)0.0004;
解:(1)∵
,∴64的平方根为±8;
(2)∵
,∴
的平方根为
;
(3)∵
,∴0.0004的平方根为±0.02;
(4)∵
,∴
的平方根为
±25;
(5)11的平方根是
.
例题讲解
运用平方运算求一个非负数的平方根是常用的方法,如被开方数是小数,要注意小数点的位置,也可先将小数化为分数,再求它的平方根,如被开方数是带分数,先要把它化为假分数.
注意:要弄清
,
,
的意义,
不能用来表示a的平方根,如:64的平方根不要写成
.
方法总结
与
的性质
64
a
活动探究一:计算下列的式子,你发现了什么?
7.2
对于正数a,
的性质
一般地,
=a
(a
≥0).
探究新知
5
5
0.7
0.7
|
a
|
a
(a
≥
0)
-a
(a
<
0)
活动探究二:计算下列的式子,你发现了什么?
的性质
探究新知
区别
与
.
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
∣a∣
不一定相等,只有当a≥0时,它们才相等.
当a<0
时,
没有意义.
之间有什么关系?一定相等吗?
与
归纳总结
1.选择题
(1)算术平方根等于它本身的数是(
)
A.0
B.1
C.0和1
D.0和±1
(2)下列叙述中正确的是(
)
A.(-11)2
的算术平方根是±11
B.大于零而小于1的数的算术平方根比原数大
C.大于零而小于1的数的平方根比原数大
D.任何一个非负数的平方根都是非负数
(3)若a2=4,b2=9,且ab<0,则a-b的值为(
)
A.-2
B.±5
C.-5
D.5
C
B
B
课堂练习
2.填空题
(1)化简:
=
.
(2)如果x2=10.222,那么x=________.
(3)若一个正数的平方根是2a-1和-a+2,则a=
,这个正数是
.
(4)有下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有平方根;④-7是49的算术平方根,其中正确的序号有:
.
π-3
-1
9
①③
±10.22
4.下列说法不正确的是______
A.0的平方根是0
B.
的平方根是2
C.非负数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
3.下列说法正确的是_________
①
-3是9的平方根;
②25的平方根是5;
③
-36的平方根是-6;
④平方根等于0的数是0;
⑤64的算术平方根是8.
①④⑤
B
5.
判断下列说法是否正确.
正确.
(4)(-4)2的平方根是-4.
(1)
是
的一个平方根;
(2)
是6的算术平方根;
(3)
的值是±4;
正确.
不正确,是4.
不正确,是±4.
6.已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是(
)
A.
a+1
B.
C.
a2+1
D.
D
7.
x为何值时,
有意义?
解:
因为
,所以
.
8.
求下列各式的值:
(1)
(2)
(3)
解:(1)
(2)
(3)
9.求下列各数的平方根
(1)1.44
,
(2)0,
(3)8
,
(4)
,
(5)441,
(6)196,
(7)10-4
10.
已知2a-1的平方根是
,3a-2b-1的平方根是±3,
求5a-3b的平方根.
解:∵
2a-1的平方根是±
,3a-2b-1的平方根是±3,
∴
2a-1=3,3a-2b-1=9.
∴
a=2.
将a=2代入3a-2b-1=9,得b=-2.
∴±
=
±
=±4,
∴
5a-3b的平方根是±4.
如果
,那么
就叫做
的平方根,记作:
当
时,
有两个平方根,即
,
表示的正平方根
,
表示负平方根。
a
|
a
|
a
(a
≥
0)
-a
(a
<
0)
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
2.2.2
平方根(2)
第二章
实数
2021-2022学年八年级数学上册同步(北师版)
1.了解平方根的概念;掌握平方根的特征。
2.能正确区分平方根与算术平方根的意义。
3.能利用开平方与平方互为逆运算的关系,求某些非负数的平方根。
学习目标
1.算术平方根
定义:若一个正数x的平方等于a,则这个数叫做a的算术平方根。
特别地,0的平方根是0,即
.
2.性质
记作:
,
表示求a的算术平方根
式子
中的双重非负性:
(1)a≥0;
(2)
≥0.
新课导入
,那么9的算术平方根是___;
,那么
的算术平方根是____;
,那么0.64的算术平方根是_____;
3
0.8
新课导入
平方根的概念及性质
问题
9的算术平方根是3,也就是说3的平方是9,还有其他数,它的平方等于9吗?
3和-3有什么特征?
由于(-3)2=9
,所以还有,这个数是-3.因此平方等于9的数有两个,3和-3.
3和-3互为相反数,会不会是巧合呢?
探究新知
(1)
0.8的平方等于0.64,那么0.64的算术平方根就是_____
(2)
的平方等于,那么的算术平方根就是____
(3)
展厅地面为正方形,其面积是49
m2,则其边长为___m.
0.8
7
做一做,想一想
问题
平方等于0.64,,49的数还有吗?
探究新知
(
)2
=
(
)2
=
(
)2
=
(
)2
=
(
)2
=
9
0.64
9
(
)?
=
0.64
3
-3
0.8
-0.8
(
)2
=
(
)2
=
(
)2
=
±3
±0.8
9
0.64
填一填
探究新知
一般地,如果一个数x的平方等于a,即x2=
a,那么这个数叫做a
的平方根(也叫二次方根).
记作:
读作:正负根号a
.
平方根
例:
∵
(±5)2=25
∴
5是25的算术平方根,即
±
=
±5
(
2可以省略)
概念学习
1.
144的平方根是什么?
2.
0的平方根是什么?
3.
的平方根是什么?
4.
-4有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
针对练习
通过这些题目的解答,你能发现什么?
问题:(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
想一想
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
只有非负数才有平方根
(算术平方根)
一个正数a的两个平方根互为相反数
正平方根:
负平方根:
平方根的性质:
归纳总结
平方根
算术平方根
联
系
区
别
平方根与算术平方根的联系与区别
一个正数有两个平方根,其中正平方根就是算术平方根
包含关系
相同性
只有非负数才有平方根和算术平方根
0的平方根和算术平方根都是0.
表示方法不同
个数不同
正数有两个平方根
正数只有一个算术平方根
归纳总结
开平方及相关运算
+1
-1
+2
-2
+3
-3
1
4
9
平方
已知一个数,求它的平方的运算,叫作平方运算.
探究新知
+1
-1
+2
-2
+3
-3
1
4
9
?运算
反之,已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
探究新知
开平方与平方是什么关系?
a的平方根
底数
幂
被开方数
互为
逆运算
指数
根号
已知底数和指数求幂
已知幂和指数求底数
开平方运算
平方运算
归纳总结
开平方与平方的对比
正数与零
任何数
幂
平方根
开
方
平
方
运算符号
适用范围
运算结果名称
性
质
正数有
个平方根,它们是
,
零的平方根是
,
负数
.
正数的平方是
数;
零的平方是
;
负数的平方是
数.
正
正
0
2
0
没有平方根
互为相反数
归纳总结
例1
求下列各数的平方根:
(1)64
;
(2)
(4)
(5)
11.
(3)0.0004;
解:(1)∵
,∴64的平方根为±8;
(2)∵
,∴
的平方根为
;
(3)∵
,∴0.0004的平方根为±0.02;
(4)∵
,∴
的平方根为
±25;
(5)11的平方根是
.
例题讲解
运用平方运算求一个非负数的平方根是常用的方法,如被开方数是小数,要注意小数点的位置,也可先将小数化为分数,再求它的平方根,如被开方数是带分数,先要把它化为假分数.
注意:要弄清
,
,
的意义,
不能用来表示a的平方根,如:64的平方根不要写成
.
方法总结
与
的性质
64
a
活动探究一:计算下列的式子,你发现了什么?
7.2
对于正数a,
的性质
一般地,
=a
(a
≥0).
探究新知
5
5
0.7
0.7
|
a
|
a
(a
≥
0)
-a
(a
<
0)
活动探究二:计算下列的式子,你发现了什么?
的性质
探究新知
区别
与
.
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
∣a∣
不一定相等,只有当a≥0时,它们才相等.
当a<0
时,
没有意义.
之间有什么关系?一定相等吗?
与
归纳总结
1.选择题
(1)算术平方根等于它本身的数是(
)
A.0
B.1
C.0和1
D.0和±1
(2)下列叙述中正确的是(
)
A.(-11)2
的算术平方根是±11
B.大于零而小于1的数的算术平方根比原数大
C.大于零而小于1的数的平方根比原数大
D.任何一个非负数的平方根都是非负数
(3)若a2=4,b2=9,且ab<0,则a-b的值为(
)
A.-2
B.±5
C.-5
D.5
C
B
B
课堂练习
2.填空题
(1)化简:
=
.
(2)如果x2=10.222,那么x=________.
(3)若一个正数的平方根是2a-1和-a+2,则a=
,这个正数是
.
(4)有下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有平方根;④-7是49的算术平方根,其中正确的序号有:
.
π-3
-1
9
①③
±10.22
4.下列说法不正确的是______
A.0的平方根是0
B.
的平方根是2
C.非负数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
3.下列说法正确的是_________
①
-3是9的平方根;
②25的平方根是5;
③
-36的平方根是-6;
④平方根等于0的数是0;
⑤64的算术平方根是8.
①④⑤
B
5.
判断下列说法是否正确.
正确.
(4)(-4)2的平方根是-4.
(1)
是
的一个平方根;
(2)
是6的算术平方根;
(3)
的值是±4;
正确.
不正确,是4.
不正确,是±4.
6.已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是(
)
A.
a+1
B.
C.
a2+1
D.
D
7.
x为何值时,
有意义?
解:
因为
,所以
.
8.
求下列各式的值:
(1)
(2)
(3)
解:(1)
(2)
(3)
9.求下列各数的平方根
(1)1.44
,
(2)0,
(3)8
,
(4)
,
(5)441,
(6)196,
(7)10-4
10.
已知2a-1的平方根是
,3a-2b-1的平方根是±3,
求5a-3b的平方根.
解:∵
2a-1的平方根是±
,3a-2b-1的平方根是±3,
∴
2a-1=3,3a-2b-1=9.
∴
a=2.
将a=2代入3a-2b-1=9,得b=-2.
∴±
=
±
=±4,
∴
5a-3b的平方根是±4.
如果
,那么
就叫做
的平方根,记作:
当
时,
有两个平方根,即
,
表示的正平方根
,
表示负平方根。
a
|
a
|
a
(a
≥
0)
-a
(a
<
0)
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
