2021--2022学年人教版七年级数学上册1.2.4绝对值课件(26张PPT)
文档属性
| 名称 | 2021--2022学年人教版七年级数学上册1.2.4绝对值课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 257.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
绝对值
学习目标
1.理解绝对值的概念及其几何意义,通过从数形两个方面理解绝对值意义,初步了解数形结合的思想方法;
2.
会求一个数的绝对值,知道一个数的绝对值,会求这个数;
3.能求一个数的绝对值和相反数,会利用绝对值比较两个负数的大小.
重难点
绝对值的概念;
绝对值的几何意义。
重点:
难点:
规定了原点、正方向、单位长度的直线。
只有符号不同的两个数互为相反数。
a
-
a
相反数
规定:0的相反数是0。
1、什么叫数轴?
2、什么叫相反数?
3、怎样表示a的相反数?
温故知新
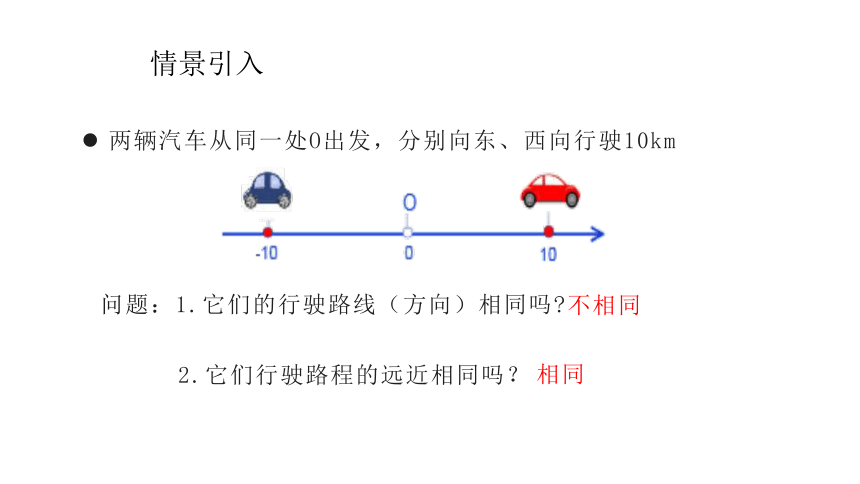
两辆汽车从同一处O出发,分别向东、西向行驶10km
问题:1.它们的行驶路线(方向)相同吗?
不相同
2.它们行驶路程的远近相同吗?
相同
情景引入
10
10
A
O
B
0
10
-10
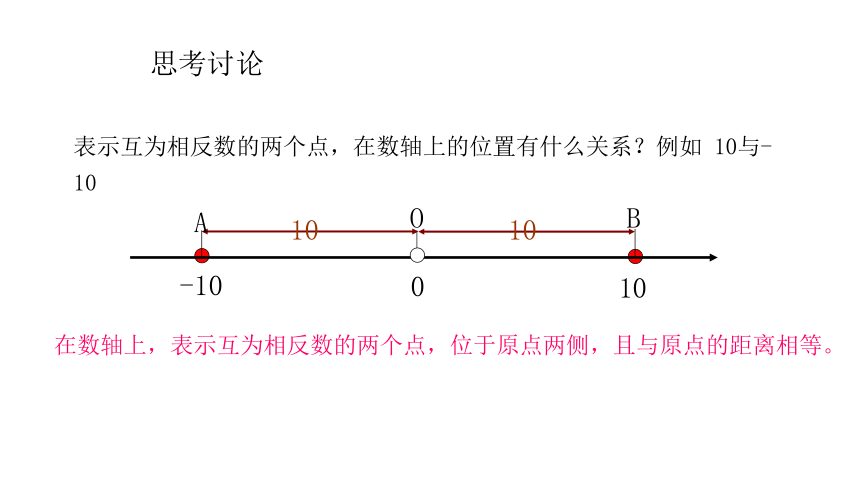
表示互为相反数的两个点,在数轴上的位置有什么关系?例如
10与-10
在数轴上,表示互为相反数的两个点,位于原点两侧,且与原点的距离相等。
思考讨论
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
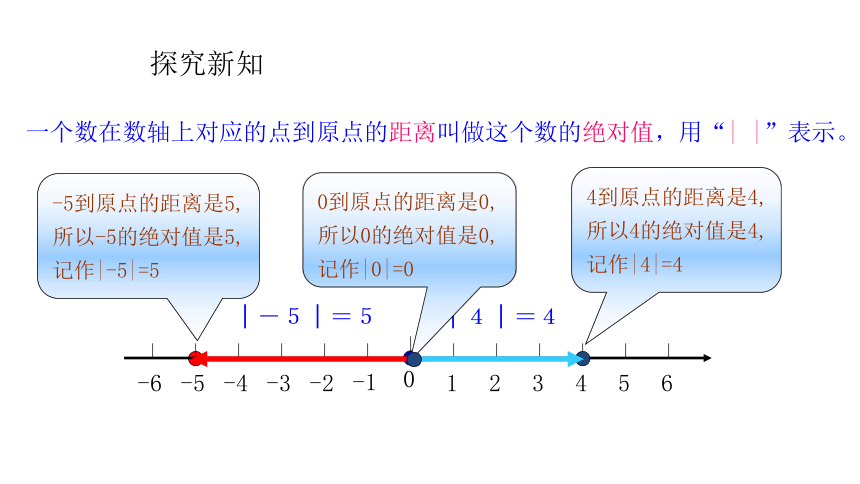
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“|
|”表示。
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
探究新知
数轴上表示数的点到原点的距离只与这个点离开原点的单位长度有关,而与它所表示的数的正负性无关
表示一个数的点与原点的距离越远,这个数的绝对值越大,离原点的距离越近,这个数的绝对值越小
距离不可能是负数,所以任何数的绝对值都是非负数,即│a│≥0
概念解读
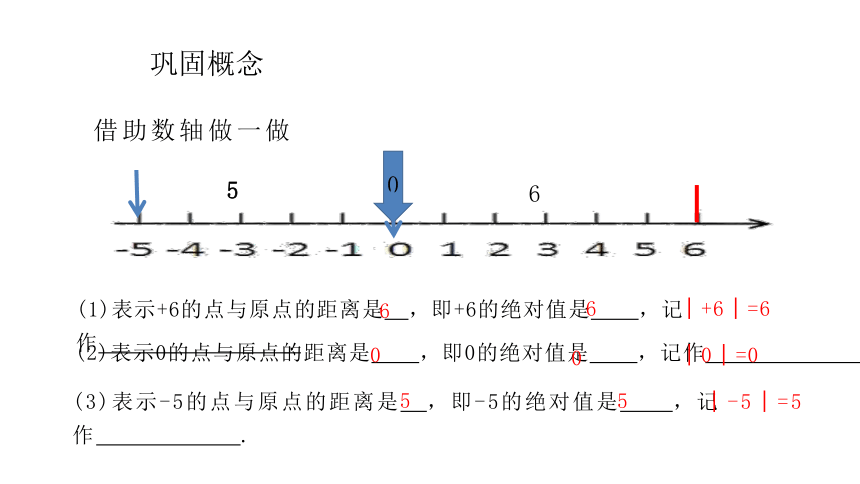
借助数轴做一做
6
0
5
(1)表示+6的点与原点的距离是
,即+6的绝对值是
,记作
.
(3)表示-5的点与原点的距离是
,即-5的绝对值是
,记作
.
(2)表示0的点与原点的距离是
,即0的绝对值是
,记作
.
6
6
│+6│=6
0
0
│0│=0
5
5
│-5│=5
巩固概念
0的绝对值是0
正数的绝对值是它本身
负数的绝对值是它的相反数
归纳总结
1.判断下列说法是否正确:
(1)一个数的绝对值越大,表示它的点在数轴上越靠右(
)
(2)一个数的绝对值越大,表示它的点在数轴上离原点越(
)
(3)当a≠0,│a│总大于0
(
)
×
√
√
课堂练习
(1)
│6│=
;
(2)
│-100│=
(3)
│0│=
│-
│=
(4)
│3.9│=
(5)
│-12│=
(6)
6
100
0
3.9
12
2.填空:
课堂练习
求一个数的绝对值的方法:
方法1:首先确定这个数的符号,然后根据“一个正数的绝对值是本身,一个负数的绝对值是它的相反数,0的绝对值是0
方法2:根据绝对值的几何意义求解,即这个数离原点的距离是多少,则它的绝对值就是多少
解题总结
3.(
1
)在数轴上表示下列各数,并比较它们的大小:
-
1.5
,
-
3
,
-
1
,
-
5
(
2
)
求出(1)中各数的绝对值,并比较它们的大小
(3)你发现了什么?
课堂练习
解:(1)
-5<-3<-1.5<-1
(2)|-1.5|=1.5;
|-3|=3;
|-1|=1
;
|-
5|=5.
(3)由以上知:正数大于0,0大于负数,正数大于负数
两个负数比较大小,绝对值大的反而小
1
<1.5<3<5
课堂练习
解法一(利用绝对值比较两个负数的大小)
解:
(1)
|
-1|=1,|
-5
|=5
,1﹤5,所以-1>-
5
4.
比较下列每组数的大小
(1)-1和–5;
(2)-
和-2.7
(2)因为|
-
|
=
,|-
2.7|
=2.7,
﹤2.7,所以
-
﹥-2.7
课堂练习
解法二
(利用数轴比较两个负数的大小)
(2)
解:(1)
因为-2.7在-
的左边,所以-2.7﹤-
因为-5在-1左边,
所以-5﹤-1
课堂练习
1.已知│a│=2
求a
已知一个数的绝对值求这个数,根据绝对值的几何意义去分析,即绝对值等于一个正数的数有两个,它们互为相反数,绝对值为0的数只有0
因为│a│=2
所以a=±2
解:
拓展提升
绝对值具有非负性,即若│a│+│b│=0,则必有
a=b=0
2.若整数a,b满足等式
,求a+b的值.
解:
审题关键:若几个非负数的和等于0,则这几个非负数同时为0
因为
所以a-3=0
,b-2=0
所以a=3,b=2
所以a+b=3+2=5
拓展提升
利用绝对值解决问题:
3.某汽车配件厂生产一批圆形的橡胶垫,从中抽取6件进行检验,比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数,检查记录如下(单位:mm)
1
2
3
4
5
6
+0.5
-0.3
+0.1
0
-0.1
+0.2
解:
因为
0<0.1<0.2<0.3<0.5
拓展提升
所以3号4号5号橡胶圈的质量相对好些
利用绝对值知识可以表示产品的质量与标准接近的程度,在所有测量数据与标准数据中的差中,绝对值越小,测量数据就与标准数据越接近;绝对值越大,测量数据就与标准数据相差越大
1
2
3
4
5
6
+0.5
-0.3
+0.1
0
-0.1
+0.2
拓展提升
4.某巡警骑摩托车在一条南北大道上来回巡逻,一条早晨,他从岗亭出发,中午停留在A处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:km)+5,-4,+3,-7,+4,-8,+2.-1,则该巡警骑摩托车共行驶了多少千米?
利用绝对值解决问题:
解:|+5|+|-4|+|+3|+|-7|+|+4|+|-8|+|+2|+|-1|
=5+4+3+7+4+8+2+1
=34
答:
该巡警骑摩托车共行驶了34千米.
计算路程时要加上绝对值
拓展提升
5.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是哪个.
解:因为|﹣0.6|<|+0.7|<|+2.5|<|﹣3.5|,
所以﹣0.6最接近标准,
所以③号球最接近标准。
拓展提升
6.出租车一天下午以车站为出发地在东西方向的道路上运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.问:若每千米耗油0.3升,问从出发到收工时,共耗油多少升?
答:从出发到收工时,共耗油17.4升.
58×0.3=17.4(升)
拓展提升
解:|+9|+|-3|+|-5|+|+4|+|-8|+|+6|+|+-3|+|-6|+
|-4|+|+10|
=9+3+5+4+8+6+3+6+4+10
=58(千米)
1.绝对值的定义:在数轴上,一个数所对应的点与原点的距离
正数的绝对值是它本身;负数的绝对值是它的相反数;
0
的绝对值是
0.
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
2.绝对值的性质:
3.会利用绝对值比较两个负数的大小:两个负数,绝对值大的反而小.
课堂总结
谢谢
绝对值
学习目标
1.理解绝对值的概念及其几何意义,通过从数形两个方面理解绝对值意义,初步了解数形结合的思想方法;
2.
会求一个数的绝对值,知道一个数的绝对值,会求这个数;
3.能求一个数的绝对值和相反数,会利用绝对值比较两个负数的大小.
重难点
绝对值的概念;
绝对值的几何意义。
重点:
难点:
规定了原点、正方向、单位长度的直线。
只有符号不同的两个数互为相反数。
a
-
a
相反数
规定:0的相反数是0。
1、什么叫数轴?
2、什么叫相反数?
3、怎样表示a的相反数?
温故知新
两辆汽车从同一处O出发,分别向东、西向行驶10km
问题:1.它们的行驶路线(方向)相同吗?
不相同
2.它们行驶路程的远近相同吗?
相同
情景引入
10
10
A
O
B
0
10
-10
表示互为相反数的两个点,在数轴上的位置有什么关系?例如
10与-10
在数轴上,表示互为相反数的两个点,位于原点两侧,且与原点的距离相等。
思考讨论
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“|
|”表示。
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
探究新知
数轴上表示数的点到原点的距离只与这个点离开原点的单位长度有关,而与它所表示的数的正负性无关
表示一个数的点与原点的距离越远,这个数的绝对值越大,离原点的距离越近,这个数的绝对值越小
距离不可能是负数,所以任何数的绝对值都是非负数,即│a│≥0
概念解读
借助数轴做一做
6
0
5
(1)表示+6的点与原点的距离是
,即+6的绝对值是
,记作
.
(3)表示-5的点与原点的距离是
,即-5的绝对值是
,记作
.
(2)表示0的点与原点的距离是
,即0的绝对值是
,记作
.
6
6
│+6│=6
0
0
│0│=0
5
5
│-5│=5
巩固概念
0的绝对值是0
正数的绝对值是它本身
负数的绝对值是它的相反数
归纳总结
1.判断下列说法是否正确:
(1)一个数的绝对值越大,表示它的点在数轴上越靠右(
)
(2)一个数的绝对值越大,表示它的点在数轴上离原点越(
)
(3)当a≠0,│a│总大于0
(
)
×
√
√
课堂练习
(1)
│6│=
;
(2)
│-100│=
(3)
│0│=
│-
│=
(4)
│3.9│=
(5)
│-12│=
(6)
6
100
0
3.9
12
2.填空:
课堂练习
求一个数的绝对值的方法:
方法1:首先确定这个数的符号,然后根据“一个正数的绝对值是本身,一个负数的绝对值是它的相反数,0的绝对值是0
方法2:根据绝对值的几何意义求解,即这个数离原点的距离是多少,则它的绝对值就是多少
解题总结
3.(
1
)在数轴上表示下列各数,并比较它们的大小:
-
1.5
,
-
3
,
-
1
,
-
5
(
2
)
求出(1)中各数的绝对值,并比较它们的大小
(3)你发现了什么?
课堂练习
解:(1)
-5<-3<-1.5<-1
(2)|-1.5|=1.5;
|-3|=3;
|-1|=1
;
|-
5|=5.
(3)由以上知:正数大于0,0大于负数,正数大于负数
两个负数比较大小,绝对值大的反而小
1
<1.5<3<5
课堂练习
解法一(利用绝对值比较两个负数的大小)
解:
(1)
|
-1|=1,|
-5
|=5
,1﹤5,所以-1>-
5
4.
比较下列每组数的大小
(1)-1和–5;
(2)-
和-2.7
(2)因为|
-
|
=
,|-
2.7|
=2.7,
﹤2.7,所以
-
﹥-2.7
课堂练习
解法二
(利用数轴比较两个负数的大小)
(2)
解:(1)
因为-2.7在-
的左边,所以-2.7﹤-
因为-5在-1左边,
所以-5﹤-1
课堂练习
1.已知│a│=2
求a
已知一个数的绝对值求这个数,根据绝对值的几何意义去分析,即绝对值等于一个正数的数有两个,它们互为相反数,绝对值为0的数只有0
因为│a│=2
所以a=±2
解:
拓展提升
绝对值具有非负性,即若│a│+│b│=0,则必有
a=b=0
2.若整数a,b满足等式
,求a+b的值.
解:
审题关键:若几个非负数的和等于0,则这几个非负数同时为0
因为
所以a-3=0
,b-2=0
所以a=3,b=2
所以a+b=3+2=5
拓展提升
利用绝对值解决问题:
3.某汽车配件厂生产一批圆形的橡胶垫,从中抽取6件进行检验,比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数,检查记录如下(单位:mm)
1
2
3
4
5
6
+0.5
-0.3
+0.1
0
-0.1
+0.2
解:
因为
0<0.1<0.2<0.3<0.5
拓展提升
所以3号4号5号橡胶圈的质量相对好些
利用绝对值知识可以表示产品的质量与标准接近的程度,在所有测量数据与标准数据中的差中,绝对值越小,测量数据就与标准数据越接近;绝对值越大,测量数据就与标准数据相差越大
1
2
3
4
5
6
+0.5
-0.3
+0.1
0
-0.1
+0.2
拓展提升
4.某巡警骑摩托车在一条南北大道上来回巡逻,一条早晨,他从岗亭出发,中午停留在A处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:km)+5,-4,+3,-7,+4,-8,+2.-1,则该巡警骑摩托车共行驶了多少千米?
利用绝对值解决问题:
解:|+5|+|-4|+|+3|+|-7|+|+4|+|-8|+|+2|+|-1|
=5+4+3+7+4+8+2+1
=34
答:
该巡警骑摩托车共行驶了34千米.
计算路程时要加上绝对值
拓展提升
5.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是哪个.
解:因为|﹣0.6|<|+0.7|<|+2.5|<|﹣3.5|,
所以﹣0.6最接近标准,
所以③号球最接近标准。
拓展提升
6.出租车一天下午以车站为出发地在东西方向的道路上运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+10.问:若每千米耗油0.3升,问从出发到收工时,共耗油多少升?
答:从出发到收工时,共耗油17.4升.
58×0.3=17.4(升)
拓展提升
解:|+9|+|-3|+|-5|+|+4|+|-8|+|+6|+|+-3|+|-6|+
|-4|+|+10|
=9+3+5+4+8+6+3+6+4+10
=58(千米)
1.绝对值的定义:在数轴上,一个数所对应的点与原点的距离
正数的绝对值是它本身;负数的绝对值是它的相反数;
0
的绝对值是
0.
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
2.绝对值的性质:
3.会利用绝对值比较两个负数的大小:两个负数,绝对值大的反而小.
课堂总结
谢谢
