2021--2022学年人教版八年级数学上册11.1.4与三角形有关的线段的综合运用课件(24张PPT)
文档属性
| 名称 | 2021--2022学年人教版八年级数学上册11.1.4与三角形有关的线段的综合运用课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
11.1.4
与三角形有关的线段的综合运用
八年级上册
学习目标
1
2
对三角形的边和三角形的高、中线与角平分线等知识的进一步理解与综合运用
培养几何直观、以及推理能力
学习重难点
重点
难点
与三角形有关的线段的综合运用
能灵活运用与三角形有关的线段的相关知识解决问题
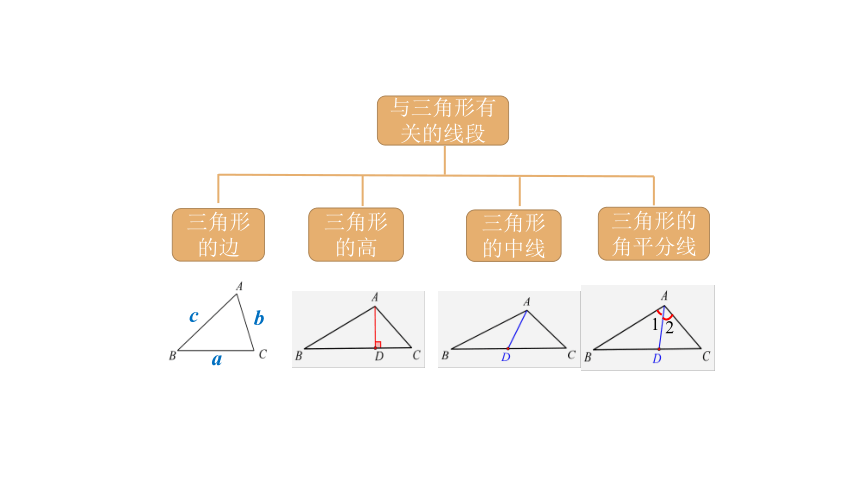
与三角形有关的线段
三角形的边
三角形的高
三角形的中线
三角形的角平分线
c
a
b
1
2
【做一做、说一说】
下列长度的三根小木棒能构成三角形的是(
)
A.2
cm,3
cm,5
cm
B.7
cm,4
cm,2
cm
C.3
cm,4
cm,8
cm
D.3
cm,3
cm,4
cm
D
知识点:三角形两边的和大于第三边.
若三条线段中a=3,b=5,c为奇数,那么由a、b、c为边组成的三角形共有( )
A.1个
B.3个
C.无数多个
D.无法确定
知识点:两边的差<第三边<两边的和
B
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为(
)
A.14
B.16
C.10
D.14或16
知识点:等腰三角形的概念.
D
思想方法:分类讨论思想.
三角形两边的和大于第三边.
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为(
)
A.14
B.16
C.10
D.14或16
D
如果把“4”改成“2”,其他条件不变,那么等腰三角形的周长为_____.
14
知识点:等腰三角形的概念.
思想方法:分类讨论思想.
三角形两边的和大于第三边.
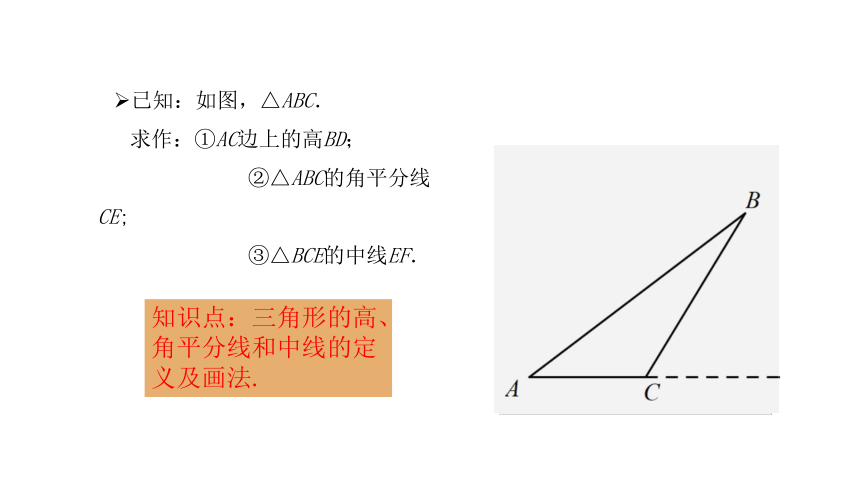
已知:如图,△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE;
③△BCE的中线EF.
知识点:三角形的高、角平分线和中线的定义及画法.
已知:如图,△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE;
③△BCE的中线EF.
知识点:三角形的高、角平分线和中线的定义及画法.
已知:如图,△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE;
③△BCE的中线EF.
知识点:三角形的高、角平分线和中线的定义及画法.
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是_____.
分析:
△ABD的周长=AB+BD+AD
△BCD的周长=BC+BD+DC
△ABD的周长-△BCD的周长
=AB-BC
在△ABC中,
∠ACB=90°,
CD是AB边上的高,
AB=13
cm,BC=12
cm,AC=5
cm,
(1)CD的长为
cm
;
(2)若AE是BC边上的中线,则△ABE的面积为
cm?.
分析:
S△ABC=
AB?CD=
BC
?AC
13CD=12×5
如图,DC是△ABC的角平分线,DE∥BC,
∠AED=80°,求∠EDC的度数.
解:
∵
DE∥BC,
∴________________________.
∵
∠AED=80°,
∴∠ACB=80°.
∵DC是△ABC的角平分线,
∴_______________.
∴_______________.
与三角形有关的线段
三角形的边
三角形的高
三角形的中线
三角形的角平分线
c
a
b
1
2
课堂小结
1.
王师傅想做一个三角形的框架,他有两根长度分别为11
cm和12
cm的细木条,需要将其中一根木条分为两段,如果不考虑损耗和接头部分,那么他可以把( )分为两截.
A.11
cm的木条
B.12
cm的木条
C.两根都可以
D.两根都不行
课后作业
2.如图所示,在△ABC中,点D,E,F是BC边上的三点,
且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线(
)
A.△ABE
B.△ADF
C.△ABC
D.△ABC
,△ADF
3.
如图,
BD和
DE分别是△ABC和△ABD的中线,若△ABC的面积为
16
cm?,则△EBD的面积为
_____
cm?.
4.如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E
,DF∥AB,DF交AC于点F
.
图中∠1与∠2有什么关系?为什么?
谢谢大家观看
11.1.4
与三角形有关的线段的综合运用
八年级上册
学习目标
1
2
对三角形的边和三角形的高、中线与角平分线等知识的进一步理解与综合运用
培养几何直观、以及推理能力
学习重难点
重点
难点
与三角形有关的线段的综合运用
能灵活运用与三角形有关的线段的相关知识解决问题
与三角形有关的线段
三角形的边
三角形的高
三角形的中线
三角形的角平分线
c
a
b
1
2
【做一做、说一说】
下列长度的三根小木棒能构成三角形的是(
)
A.2
cm,3
cm,5
cm
B.7
cm,4
cm,2
cm
C.3
cm,4
cm,8
cm
D.3
cm,3
cm,4
cm
D
知识点:三角形两边的和大于第三边.
若三条线段中a=3,b=5,c为奇数,那么由a、b、c为边组成的三角形共有( )
A.1个
B.3个
C.无数多个
D.无法确定
知识点:两边的差<第三边<两边的和
B
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为(
)
A.14
B.16
C.10
D.14或16
知识点:等腰三角形的概念.
D
思想方法:分类讨论思想.
三角形两边的和大于第三边.
已知等腰三角形一边长为4,一边长为6,则等腰三角形的周长为(
)
A.14
B.16
C.10
D.14或16
D
如果把“4”改成“2”,其他条件不变,那么等腰三角形的周长为_____.
14
知识点:等腰三角形的概念.
思想方法:分类讨论思想.
三角形两边的和大于第三边.
已知:如图,△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE;
③△BCE的中线EF.
知识点:三角形的高、角平分线和中线的定义及画法.
已知:如图,△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE;
③△BCE的中线EF.
知识点:三角形的高、角平分线和中线的定义及画法.
已知:如图,△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE;
③△BCE的中线EF.
知识点:三角形的高、角平分线和中线的定义及画法.
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
如图,
在△ABC
中,∠1=∠2,
G点为AD中点,
延长BG交AC于点E.
F为AB上一点,
CF⊥AD于H.
下面判断正确的有__________.
①
AD是△ABE的角平分线;
②
BE是△ABD的AD边上的中线;
③
CH为△ACD的AD边上的高;
④
AH是△ACF的角平分线和高线.
【想一想、做一做】
BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是_____.
分析:
△ABD的周长=AB+BD+AD
△BCD的周长=BC+BD+DC
△ABD的周长-△BCD的周长
=AB-BC
在△ABC中,
∠ACB=90°,
CD是AB边上的高,
AB=13
cm,BC=12
cm,AC=5
cm,
(1)CD的长为
cm
;
(2)若AE是BC边上的中线,则△ABE的面积为
cm?.
分析:
S△ABC=
AB?CD=
BC
?AC
13CD=12×5
如图,DC是△ABC的角平分线,DE∥BC,
∠AED=80°,求∠EDC的度数.
解:
∵
DE∥BC,
∴________________________.
∵
∠AED=80°,
∴∠ACB=80°.
∵DC是△ABC的角平分线,
∴_______________.
∴_______________.
与三角形有关的线段
三角形的边
三角形的高
三角形的中线
三角形的角平分线
c
a
b
1
2
课堂小结
1.
王师傅想做一个三角形的框架,他有两根长度分别为11
cm和12
cm的细木条,需要将其中一根木条分为两段,如果不考虑损耗和接头部分,那么他可以把( )分为两截.
A.11
cm的木条
B.12
cm的木条
C.两根都可以
D.两根都不行
课后作业
2.如图所示,在△ABC中,点D,E,F是BC边上的三点,
且∠1=∠2=∠3=∠4,AE是哪个三角形的角平分线(
)
A.△ABE
B.△ADF
C.△ABC
D.△ABC
,△ADF
3.
如图,
BD和
DE分别是△ABC和△ABD的中线,若△ABC的面积为
16
cm?,则△EBD的面积为
_____
cm?.
4.如图,AD是△ABC的角平分线,DE∥AC,DE交AB于点E
,DF∥AB,DF交AC于点F
.
图中∠1与∠2有什么关系?为什么?
谢谢大家观看
