2021--2022学年人教版九年级数学上册21.2.2.2《公式法解一元二次方程》课件(28张PPT)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册21.2.2.2《公式法解一元二次方程》课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 20:13:08 | ||
图片预览








文档简介
(共28张PPT)
21.2.2.2
公式法解一元二次方程
九年级上册
学习目标
1
2
复习求根公式,会用公式法熟练的解一元二次方程
会用公式法解简单的含字母系数的一元二次方程.
学习重难点
重点
难点
用公式法解一元二次方程
用公式法解简单的含字母系数的一元二次方程
预习检测
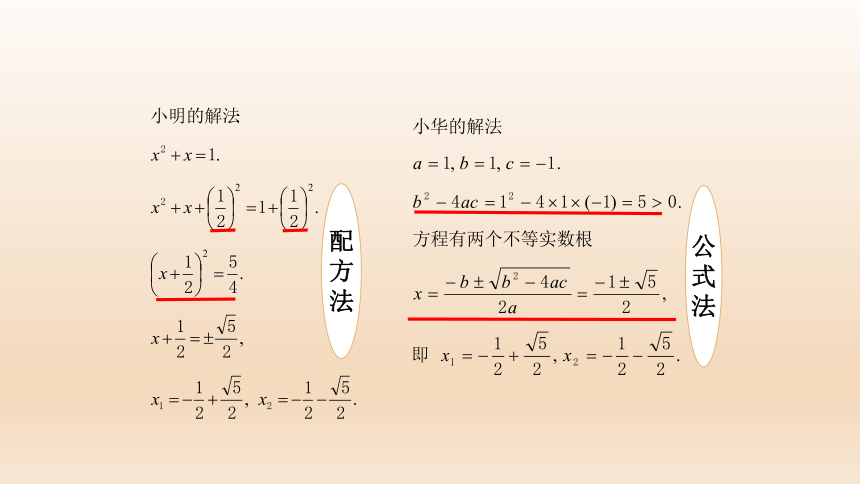
形式比较复杂的一元二次方程,我们第一步应该做什么?
请同学们解方程x2+x-1=0.
复习回顾
配方法
公式法
关于x的一元二次方程
当
时,方程的根为
当
时,方程无实数根.
当
时,方程的根为
复习回顾
例1
用公式法解下列方程:
运用公式
方程有两个相等的实数根
解:
例1
用公式法解下列方程:
方程有两个不等的实数根
解:方程化为
即
例1
用公式法解下列方程:
例1
用公式法解下列方程:
方程无实数根
.
解:方程化为
(1)化
“一般形式”.
(2)确定a,b,c(注意符号).
(3)计算b2-4ac的值.
(4)当b2-4ac≥0时
,将a,b,c及b2-4ac代入公式
(5)结果化成最简形式.
小结1:用公式法解一元二次方程的一般步骤
当b2-4ac<0时
,方程无实数根.
①
当
时,
方程有两个不等实数根
;
②
当
时,
方程有两个相等实数根
;
③
当
时,
方程无实数根
.
小结2:
关于x的一元二次方程ax2+bx+c=0(a≠0)
实数根的情况
一般的,式子
叫做一元二次方程
根的判别式,通常
用希腊字母“?”表示它,即?=
根的判别式
?
5m2是非负数
∴原方程为一元二次方程
例2
用公式法解关于x的方程:
关于x的方程
解:
方程有两个实数根
即
方程有两个实数根
例2
用公式法解关于x的方程:
解:方程化为
∴原方程为一元二次方程
即
分式化简
例1
用公式法解下列方程:
例2
用公式法解关于x的方程:
相同点:
都是一元二次方程;
用公式法都可以求出这些方程的根.
不同点:
例1是数字系数,例2是字母系数;
例1是数的运算,例2是式的运算比较多,
例1的判别式
的结果是一个数,
例2的判别式
的结果是一个式子.
课堂练习
1.关于x的一元二次方程x2-3x-k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
(2)取k=-2,x1=1,x2=2(答案不唯一)
解:(1)
课堂练习
2.在等腰△ABC中,三边分别为a,b,c,其中a=5,若关于x的方程x2+(b+2)x+6-b=0有两个相等的实数根,求△ABC的周长.
解:由Δ=(b+2)2-4(6-b)=b2+8b-20=0,
解得b=2或b=-10(不合题意,舍去),
∴b=2
(1)当c=b=2时,b+c=4<5,不合题意;
(2)当c=a=5时,周长为a+b+c=12
1.本节课,主要练习了用公式法解一元二次方程;
2.
一元二次方程根的情况与判别式的符号的关系;
3.
要熟记求根公式.
课堂小结
关于x的一元二次方程
当
时,方程的根为
;
当
时,方程无实数根.
当
时,方程的根为
;
课堂小结
用公式法解下列关于x的方程:
课后作业
解:
用公式法解下列关于x的方程:
方程有两个不等实数根
即
用公式法解下列关于x的方程:
解:
方程有两个实数根
即
谢谢大家观看
21.2.2.2
公式法解一元二次方程
九年级上册
学习目标
1
2
复习求根公式,会用公式法熟练的解一元二次方程
会用公式法解简单的含字母系数的一元二次方程.
学习重难点
重点
难点
用公式法解一元二次方程
用公式法解简单的含字母系数的一元二次方程
预习检测
形式比较复杂的一元二次方程,我们第一步应该做什么?
请同学们解方程x2+x-1=0.
复习回顾
配方法
公式法
关于x的一元二次方程
当
时,方程的根为
当
时,方程无实数根.
当
时,方程的根为
复习回顾
例1
用公式法解下列方程:
运用公式
方程有两个相等的实数根
解:
例1
用公式法解下列方程:
方程有两个不等的实数根
解:方程化为
即
例1
用公式法解下列方程:
例1
用公式法解下列方程:
方程无实数根
.
解:方程化为
(1)化
“一般形式”.
(2)确定a,b,c(注意符号).
(3)计算b2-4ac的值.
(4)当b2-4ac≥0时
,将a,b,c及b2-4ac代入公式
(5)结果化成最简形式.
小结1:用公式法解一元二次方程的一般步骤
当b2-4ac<0时
,方程无实数根.
①
当
时,
方程有两个不等实数根
;
②
当
时,
方程有两个相等实数根
;
③
当
时,
方程无实数根
.
小结2:
关于x的一元二次方程ax2+bx+c=0(a≠0)
实数根的情况
一般的,式子
叫做一元二次方程
根的判别式,通常
用希腊字母“?”表示它,即?=
根的判别式
?
5m2是非负数
∴原方程为一元二次方程
例2
用公式法解关于x的方程:
关于x的方程
解:
方程有两个实数根
即
方程有两个实数根
例2
用公式法解关于x的方程:
解:方程化为
∴原方程为一元二次方程
即
分式化简
例1
用公式法解下列方程:
例2
用公式法解关于x的方程:
相同点:
都是一元二次方程;
用公式法都可以求出这些方程的根.
不同点:
例1是数字系数,例2是字母系数;
例1是数的运算,例2是式的运算比较多,
例1的判别式
的结果是一个数,
例2的判别式
的结果是一个式子.
课堂练习
1.关于x的一元二次方程x2-3x-k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
(2)取k=-2,x1=1,x2=2(答案不唯一)
解:(1)
课堂练习
2.在等腰△ABC中,三边分别为a,b,c,其中a=5,若关于x的方程x2+(b+2)x+6-b=0有两个相等的实数根,求△ABC的周长.
解:由Δ=(b+2)2-4(6-b)=b2+8b-20=0,
解得b=2或b=-10(不合题意,舍去),
∴b=2
(1)当c=b=2时,b+c=4<5,不合题意;
(2)当c=a=5时,周长为a+b+c=12
1.本节课,主要练习了用公式法解一元二次方程;
2.
一元二次方程根的情况与判别式的符号的关系;
3.
要熟记求根公式.
课堂小结
关于x的一元二次方程
当
时,方程的根为
;
当
时,方程无实数根.
当
时,方程的根为
;
课堂小结
用公式法解下列关于x的方程:
课后作业
解:
用公式法解下列关于x的方程:
方程有两个不等实数根
即
用公式法解下列关于x的方程:
解:
方程有两个实数根
即
谢谢大家观看
同课章节目录
