2021--2022学年人教版九年级数学上册21.3.2《平均变化率与一元二次方程》课件(26张PPT)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册21.3.2《平均变化率与一元二次方程》课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 265.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
21.3.2
平均变化率与一元二次方程
九年级上册
学习目标
1
2
掌握建立解决增长率与降低率问题的数学模型
正确分析问题中的数量关系并建立一元二次方程模型
学习重难点
重点
难点
建立数学模型以解决增长率与降低率问题
正确分析问题中的数量关系并建立一元二次方程模型
预习检测
1.平均变化率问题的基本特征是什么?
?
2.在解决平均变化率问题时应注意什么?
1、解决增长率与降低率问题;
2、分析问题中的数量关系并建立一元二次方程模型.
思考
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,去年生产1吨甲种药品的成本是4650
元,则下降率是
.如果保持这个下降率,则现在生产1吨甲种药品的成本是
元.
7%
4324.5
下降率=
下降前的量-下降后的量
下降前的量
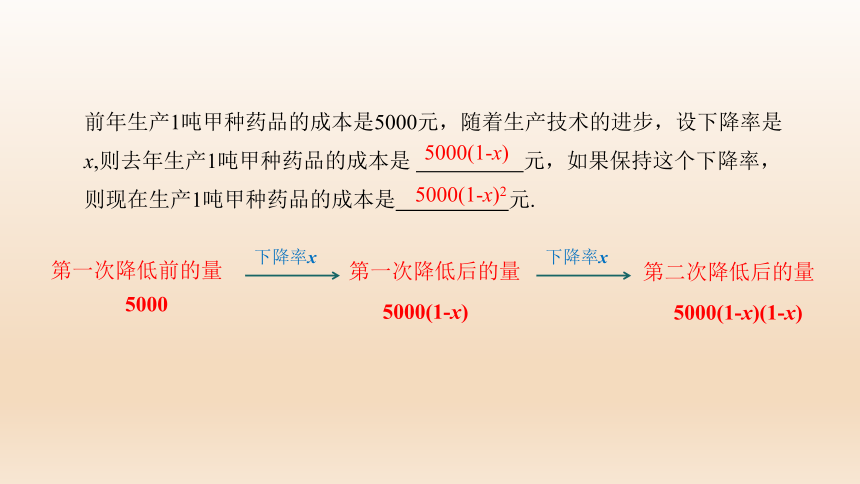
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,设下降率是x,则去年生产1吨甲种药品的成本是
元,如果保持这个下降率,则现在生产1吨甲种药品的成本是
元.
下降率x
第一次降低前的量
5000(1-x)
第一次降低后的量
5000
下降率x
第二次降低后的量
5000(1-x)(1-x)
5000(1-x)
5000(1-x)2
练习:某一商人进货价便宜8%,而售价不变,那么他的利润(按进货价而定)可由目前x增加到(x+10%),则x是(
)
A.12%
B.15%
C.30%
D.50%
B
例1
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,试求甲种药品成本的年平均下降率是多少?
解:设甲种药品的年平均下降率为x.根据题意,列方程,得
5
000
(
1-x
)2
=
3000,
解方程,得
x1≈0.225,x2≈1.775.
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
下降率不能超过1.
注意
不能.
绝对量:甲种药品成本的年平均下降额为(5000-3000)÷2=1000元,
乙种药品成本的年平均下降额为(6000-3000)÷2=1200元,
显然,乙种药品成本的年平均下降额较大.
问题1
药品年平均下降额大能否说年平均下降率(百分数)就大呢?
思考
不能.
能过上面的计算,甲、乙两种药品的年平均下降率相等.
因此我们发现虽然绝对量相差很多,但其相对量(年平均下降率)也可能相等.
问题2
从上面的绝对量的大小能否说明相对量的大小呢?也就说能否说明乙种药品成本的年平均下降率大呢?
问题3
你能总结出有关增长率和降低率的有关数量关系吗?
类似地
这种增长率的问题在实际生活中普遍存在,有一定的模式.
若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为a(1±x)n=b(其中增长取“+”,降低取“-”).
例2
某公司2017年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
分析:设这个增长率为x,则
二月份营业额为:__________.
三月份营业额为:__________.
根据:
.
作为等量关系列方程为:
200(1+x)
一月、二月、三月的营业额共950万元.
200(1+x)2
200+200(1+x)
+200(1+x)2=950
例2
某公司2017年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为x.根据题意,得
答:这个增长率为50%.
200+200(1+x)
+200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
注意
增长率不可为负,但可以超过1.
练习:上海甲商场七月份利润为100万元,九月份的利率为121万元,乙商场七月份利率为200万元,九月份的利润为288万元,那么哪个商场利润的年平均上升率较大?
解:甲:设上升率为x,
则100(1+x)2=121,x=10%
乙:设上升率为y,
则200(1+y)2=288,y=20%,
那么乙商场年均利润的上升率大.
解:设多种x棵树,则
(100+x)(1000-2x)=100×1000×(1+15.2%),
整理得:x2-400x+7600=0,
(x-20)(x-380)=0,
解得x1=20,x2=380
练习:某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,如果要使产量增加15.2%,那么应多种多少棵桃树?
1.某厂今年一月份的总产量为500吨,三月份的总产量为720吨,平均每月增长率是x,列方程(
)
A.500(1+2x)=720
B.500(1+x)2=720
C.500(1+x2)=720
D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程为
.
B
2(1+x)+2(1+x)2=8
课堂练习
3.青山村种的水稻2013年平均每公顷产7200千克,2014年平均每公顷产8712千克,求水稻每公顷产量的年平均增长率.
解:设水稻每公顷产量的平均增长率为x,
根据题意,得
系数化为1得,
直接开平方得,
则
答:水稻每公顷产量的年平均增长率为10%.
7200(1+x)2=8712
(1+x)2=1.21
1+x=1.1,
1+x=-1.1
x1=0.1,
x2=-1.1,
1.某村2016年的人均收入为20
000元,2018年的人均收入为24
200元.
(1)求2016年到2018年该村人均收入的年平均增长率;
解:设2016年到2018年该村人均收入的年平均增长率为x,
根据题意得20
000(1+x)2=24
200,
解得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:2016年到2018年该村人均收入的年平均增长率为10%.
拓展提高
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年该村的人均收入是多少元?
解:24
200×(1+10%)=26
620(元).
答:预测2019年该村的人均收入是26
620元.
2.为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个电子产品的固定成本为100元,问这种电子产品降价后的销售单价为多少元时,公司每天可获利32
000元?
解:设降价后的销售单价为x元,则降价后每天可售出[300+5(200-x)]个,
依题意,得(x-100)[300+5(200-x)]=32
000,
整理,得x2-360x+32
400=0,
解得x1=x2=180,180<200,符合题意.
答:这种电子产品降价后的销售单价为180元时,公司每天可获利32
000元.
3.某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
解:设该养殖场蛋鸡产蛋量的月平均增长率为x,
根据题意得,2.5(1+x)2=3.6,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:该养殖场蛋鸡产蛋量的月平均增长率为20%.
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg,如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
课堂小结
平均变化率问题
增长率问题
a(1+x)2=b,其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.
降低率问题
a(1-x)2=b,其中a为降低前的量,x为降低率,2为降低次数,b为降低后的量.注意1与x位置不可调换.
课后作业
1.某印刷厂第一季度共印了182万册书,一月份印了50万册,那么该印刷厂第一季度印书的月平均增长率是多少?
2.生产某电器,原来每件的成本是300元,由于技术革新,连续两次降低成本,现在的成本是192元.
每次降低成本时,成本的平均降低率是多少?
谢谢大家观看
21.3.2
平均变化率与一元二次方程
九年级上册
学习目标
1
2
掌握建立解决增长率与降低率问题的数学模型
正确分析问题中的数量关系并建立一元二次方程模型
学习重难点
重点
难点
建立数学模型以解决增长率与降低率问题
正确分析问题中的数量关系并建立一元二次方程模型
预习检测
1.平均变化率问题的基本特征是什么?
?
2.在解决平均变化率问题时应注意什么?
1、解决增长率与降低率问题;
2、分析问题中的数量关系并建立一元二次方程模型.
思考
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,去年生产1吨甲种药品的成本是4650
元,则下降率是
.如果保持这个下降率,则现在生产1吨甲种药品的成本是
元.
7%
4324.5
下降率=
下降前的量-下降后的量
下降前的量
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,设下降率是x,则去年生产1吨甲种药品的成本是
元,如果保持这个下降率,则现在生产1吨甲种药品的成本是
元.
下降率x
第一次降低前的量
5000(1-x)
第一次降低后的量
5000
下降率x
第二次降低后的量
5000(1-x)(1-x)
5000(1-x)
5000(1-x)2
练习:某一商人进货价便宜8%,而售价不变,那么他的利润(按进货价而定)可由目前x增加到(x+10%),则x是(
)
A.12%
B.15%
C.30%
D.50%
B
例1
前年生产1吨甲种药品的成本是5000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,试求甲种药品成本的年平均下降率是多少?
解:设甲种药品的年平均下降率为x.根据题意,列方程,得
5
000
(
1-x
)2
=
3000,
解方程,得
x1≈0.225,x2≈1.775.
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
下降率不能超过1.
注意
不能.
绝对量:甲种药品成本的年平均下降额为(5000-3000)÷2=1000元,
乙种药品成本的年平均下降额为(6000-3000)÷2=1200元,
显然,乙种药品成本的年平均下降额较大.
问题1
药品年平均下降额大能否说年平均下降率(百分数)就大呢?
思考
不能.
能过上面的计算,甲、乙两种药品的年平均下降率相等.
因此我们发现虽然绝对量相差很多,但其相对量(年平均下降率)也可能相等.
问题2
从上面的绝对量的大小能否说明相对量的大小呢?也就说能否说明乙种药品成本的年平均下降率大呢?
问题3
你能总结出有关增长率和降低率的有关数量关系吗?
类似地
这种增长率的问题在实际生活中普遍存在,有一定的模式.
若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为a(1±x)n=b(其中增长取“+”,降低取“-”).
例2
某公司2017年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
分析:设这个增长率为x,则
二月份营业额为:__________.
三月份营业额为:__________.
根据:
.
作为等量关系列方程为:
200(1+x)
一月、二月、三月的营业额共950万元.
200(1+x)2
200+200(1+x)
+200(1+x)2=950
例2
某公司2017年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
解:设这个增长率为x.根据题意,得
答:这个增长率为50%.
200+200(1+x)
+200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
注意
增长率不可为负,但可以超过1.
练习:上海甲商场七月份利润为100万元,九月份的利率为121万元,乙商场七月份利率为200万元,九月份的利润为288万元,那么哪个商场利润的年平均上升率较大?
解:甲:设上升率为x,
则100(1+x)2=121,x=10%
乙:设上升率为y,
则200(1+y)2=288,y=20%,
那么乙商场年均利润的上升率大.
解:设多种x棵树,则
(100+x)(1000-2x)=100×1000×(1+15.2%),
整理得:x2-400x+7600=0,
(x-20)(x-380)=0,
解得x1=20,x2=380
练习:某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,如果要使产量增加15.2%,那么应多种多少棵桃树?
1.某厂今年一月份的总产量为500吨,三月份的总产量为720吨,平均每月增长率是x,列方程(
)
A.500(1+2x)=720
B.500(1+x)2=720
C.500(1+x2)=720
D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程为
.
B
2(1+x)+2(1+x)2=8
课堂练习
3.青山村种的水稻2013年平均每公顷产7200千克,2014年平均每公顷产8712千克,求水稻每公顷产量的年平均增长率.
解:设水稻每公顷产量的平均增长率为x,
根据题意,得
系数化为1得,
直接开平方得,
则
答:水稻每公顷产量的年平均增长率为10%.
7200(1+x)2=8712
(1+x)2=1.21
1+x=1.1,
1+x=-1.1
x1=0.1,
x2=-1.1,
1.某村2016年的人均收入为20
000元,2018年的人均收入为24
200元.
(1)求2016年到2018年该村人均收入的年平均增长率;
解:设2016年到2018年该村人均收入的年平均增长率为x,
根据题意得20
000(1+x)2=24
200,
解得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:2016年到2018年该村人均收入的年平均增长率为10%.
拓展提高
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年该村的人均收入是多少元?
解:24
200×(1+10%)=26
620(元).
答:预测2019年该村的人均收入是26
620元.
2.为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个电子产品的固定成本为100元,问这种电子产品降价后的销售单价为多少元时,公司每天可获利32
000元?
解:设降价后的销售单价为x元,则降价后每天可售出[300+5(200-x)]个,
依题意,得(x-100)[300+5(200-x)]=32
000,
整理,得x2-360x+32
400=0,
解得x1=x2=180,180<200,符合题意.
答:这种电子产品降价后的销售单价为180元时,公司每天可获利32
000元.
3.某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
解:设该养殖场蛋鸡产蛋量的月平均增长率为x,
根据题意得,2.5(1+x)2=3.6,
解得x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:该养殖场蛋鸡产蛋量的月平均增长率为20%.
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg,如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
课堂小结
平均变化率问题
增长率问题
a(1+x)2=b,其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.
降低率问题
a(1-x)2=b,其中a为降低前的量,x为降低率,2为降低次数,b为降低后的量.注意1与x位置不可调换.
课后作业
1.某印刷厂第一季度共印了182万册书,一月份印了50万册,那么该印刷厂第一季度印书的月平均增长率是多少?
2.生产某电器,原来每件的成本是300元,由于技术革新,连续两次降低成本,现在的成本是192元.
每次降低成本时,成本的平均降低率是多少?
谢谢大家观看
同课章节目录
