3.7 二次函数与一元二次方程 课件(共33张PPT)
文档属性
| 名称 | 3.7 二次函数与一元二次方程 课件(共33张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 18:22:43 | ||
图片预览










文档简介
(共33张PPT)
第三章
二次函数
7
二次函数与一元二次方程的关系
知识点一
二次函数与一元二次方程的关系
当y=0时,二次函数y=ax2+bx+c(a≠0)就成为一元二次方程ax2+bx+c=0(a≠0).方程若有解,其解就是抛物线y=ax2+bx+c(a≠0)与x轴(即直线y=0)交点的横坐标.因此有如下关系:
当b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有两个交点;
当b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴有一个交点;
当b2-4ac<0时,方程没有实数根,抛物线与x轴没有交点.
知识拓展
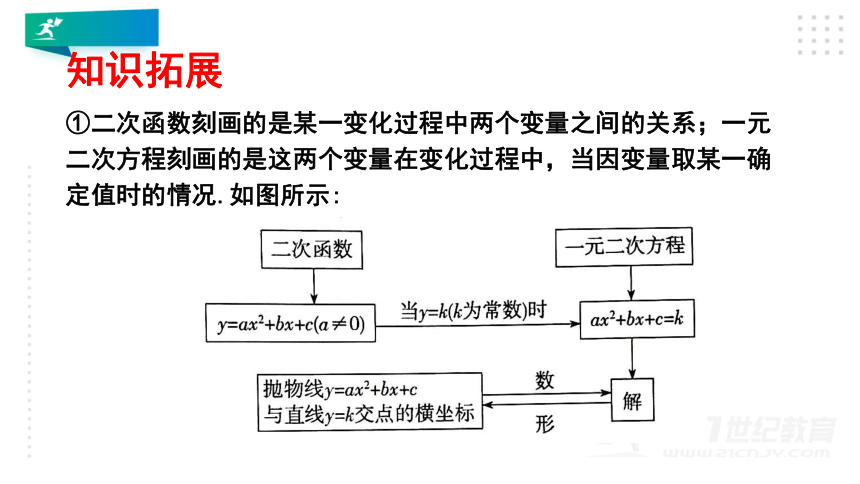
①二次函数刻画的是某一变化过程中两个变量之间的关系;一元二次方程刻画的是这两个变量在变化过程中,当因变量取某一确定值时的情况.如图所示:
知识拓展
例1
抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是__________.
例1
抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是__________.
解析:
∵△=[2(k-1)]2-4×2×(-k)=4k2+4>0,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点.
例1
抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是__________.
解析:
∵△=[2(k-1)]2-4×2×(-k)=4k2+4>0,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点.
故答案为
2.
例2
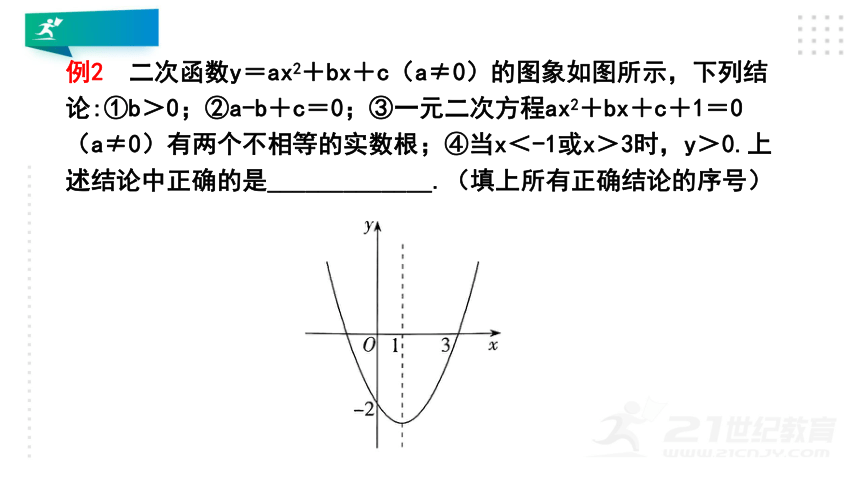
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b>0;②a-b+c=0;③一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;④当x<-1或x>3时,y>0.上述结论中正确的是_____________.(填上所有正确结论的序号)
解析
由题图可知,对称轴为直线x=1,与x轴的一个交点坐标为(3,0),
∴b=-2a,抛物线与x轴的另一个交点的坐标为(-1,0).
∵a>0,∴b<0,∴①错误;
当x=-1时,y=0,即a-b+c=0,∴②正确;
一元二次方程ax2+bx+c+1=0(a≠0)可以看成是函数y=ax2+bx+c的图象与直线y=-1的交点,
由图象可知函数y=ax2+bx+c的图象与直线y=-1有两个不同的交点,
∴一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根∴③正确;
由题图可知,当x<-1或x>3时,y>0,∴④正确.
解析
由题图可知,对称轴为直线x=1,与x轴的一个交点坐标为(3,0),
∴b=-2a,抛物线与x轴的另一个交点的坐标为(-1,0).
∵a>0,∴b<0,∴①错误;
当x=-1时,y=0,即a-b+c=0,∴②正确;
一元二次方程ax2+bx+c+1=0(a≠0)可以看成是函数y=ax2+bx+c的图象与直线y=-1的交点,
由图象可知函数y=ax2+bx+c的图象与直线y=-1有两个不同的交点,
∴一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根∴③正确;
由题图可知,当x<-1或x>3时,y>0,∴④正确.
答案
②③④
方法归纳
数形的有机结合与灵活转换是解决此类题的关键.
知识点二
利用二次函数的图象求一元二次方程的近似根
由二次函数与一元二次方程的关系,可以用图象估算一元二次方程的根步骤:先利用图象大致求出一元二次方程的根的取值范围,再借助计算器利用两头夹逼的方法探索,逐步缩小方程根的取值范围,最终确定方程的近似根.
温馨提示
通过画函数的图象解一元二次方程可使解题过程直观化,但存在作图的误差,因此通过这种方法求得的方程的解一般是近似的.
例3
用图象法求一元二次方程x2-2x-1=0的近似解(精确到0.1).
解析
令y=x2-2x-1,则y=(x-1)2-2,其对称轴为直线x=1,顶点坐标为(1,-2).
列表如下:
描点、连线,图象如图所示.
由图象知方程有两个根,一个在-0.5和0之间,另一个在2和2.5之间,易知当x=-0.4或x=2.4时,y≈0.因此方程x2-2x-1=0的解的近似值为-0.4或2.4.
X
-1
-0.5
0
1
2
2.5
3
y
2
0.25
-1
-2
-1
0.25
2
点拨
图象法解方程(组)是一种直观法,其实质是观察交点坐标,即观察抛物线与x轴(即直线y=0)的交点.
经典例题
题型一
根据抛物线与直线的交点情况,求字母的取值(范围)
例1
已知关于x的二次函数y=(a-1)x2-2x+3的图象与坐标轴有两个交点,则a的值是____________.
题型一
根据抛物线与直线的交点情况,求字母的取值(范围)
题型一
根据抛物线与直线的交点情况,求字母的取值(范围)
方法归纳
根据二次函数的图象与直线y=m(m为常数)的交点情况,求有关字母的值或取值范围时,解题方法是根据对应的一元二次方程的根的情况,利用根的判别式列方程或不等式求解注意:若未说明函数是哪种类型的函数,还需分情况讨论.
题型二
根据二次函数的图象求解一元二次方程或不等式
例2
抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过A(2,0),B(-4,0)两点,下列四个结论:
①一元二次方程ax2+bx+c=0的根为x1=2,x2=-4;
②若点C(-5,y1),D(m,y2)在该抛物线上,则y1<y2;
③对于任意实数t,总有at2+bt≤a-b;
④对于a的每一个确定值,若一元二次方程ax2+bx+c=p(p为常数,p>0)的根为整数,则p的值只有两个.
其中正确的结论是___________(填写序号).
方法归纳
易错易混
易错点
考虑不周,忽略分类讨论
判断函数图象与坐标轴的交点,要考虑两种情况,一是若函数是一次函数,则函数图象与坐标轴必有交点;二是若函数是二次函数,要分与x轴相交、与y轴相交两种情况讨论抛物线与y轴必有一交点,与x轴的交点则由b2-4ac决定注意不要忽略抛物线与y轴必有交点的情况.
例
若函数y=mx2+x+1的图象与x轴只有一个公共点,则m的值是__________.
第三章
二次函数
7
二次函数与一元二次方程的关系
知识点一
二次函数与一元二次方程的关系
当y=0时,二次函数y=ax2+bx+c(a≠0)就成为一元二次方程ax2+bx+c=0(a≠0).方程若有解,其解就是抛物线y=ax2+bx+c(a≠0)与x轴(即直线y=0)交点的横坐标.因此有如下关系:
当b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有两个交点;
当b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴有一个交点;
当b2-4ac<0时,方程没有实数根,抛物线与x轴没有交点.
知识拓展
①二次函数刻画的是某一变化过程中两个变量之间的关系;一元二次方程刻画的是这两个变量在变化过程中,当因变量取某一确定值时的情况.如图所示:
知识拓展
例1
抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是__________.
例1
抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是__________.
解析:
∵△=[2(k-1)]2-4×2×(-k)=4k2+4>0,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点.
例1
抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是__________.
解析:
∵△=[2(k-1)]2-4×2×(-k)=4k2+4>0,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点.
故答案为
2.
例2
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b>0;②a-b+c=0;③一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;④当x<-1或x>3时,y>0.上述结论中正确的是_____________.(填上所有正确结论的序号)
解析
由题图可知,对称轴为直线x=1,与x轴的一个交点坐标为(3,0),
∴b=-2a,抛物线与x轴的另一个交点的坐标为(-1,0).
∵a>0,∴b<0,∴①错误;
当x=-1时,y=0,即a-b+c=0,∴②正确;
一元二次方程ax2+bx+c+1=0(a≠0)可以看成是函数y=ax2+bx+c的图象与直线y=-1的交点,
由图象可知函数y=ax2+bx+c的图象与直线y=-1有两个不同的交点,
∴一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根∴③正确;
由题图可知,当x<-1或x>3时,y>0,∴④正确.
解析
由题图可知,对称轴为直线x=1,与x轴的一个交点坐标为(3,0),
∴b=-2a,抛物线与x轴的另一个交点的坐标为(-1,0).
∵a>0,∴b<0,∴①错误;
当x=-1时,y=0,即a-b+c=0,∴②正确;
一元二次方程ax2+bx+c+1=0(a≠0)可以看成是函数y=ax2+bx+c的图象与直线y=-1的交点,
由图象可知函数y=ax2+bx+c的图象与直线y=-1有两个不同的交点,
∴一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根∴③正确;
由题图可知,当x<-1或x>3时,y>0,∴④正确.
答案
②③④
方法归纳
数形的有机结合与灵活转换是解决此类题的关键.
知识点二
利用二次函数的图象求一元二次方程的近似根
由二次函数与一元二次方程的关系,可以用图象估算一元二次方程的根步骤:先利用图象大致求出一元二次方程的根的取值范围,再借助计算器利用两头夹逼的方法探索,逐步缩小方程根的取值范围,最终确定方程的近似根.
温馨提示
通过画函数的图象解一元二次方程可使解题过程直观化,但存在作图的误差,因此通过这种方法求得的方程的解一般是近似的.
例3
用图象法求一元二次方程x2-2x-1=0的近似解(精确到0.1).
解析
令y=x2-2x-1,则y=(x-1)2-2,其对称轴为直线x=1,顶点坐标为(1,-2).
列表如下:
描点、连线,图象如图所示.
由图象知方程有两个根,一个在-0.5和0之间,另一个在2和2.5之间,易知当x=-0.4或x=2.4时,y≈0.因此方程x2-2x-1=0的解的近似值为-0.4或2.4.
X
-1
-0.5
0
1
2
2.5
3
y
2
0.25
-1
-2
-1
0.25
2
点拨
图象法解方程(组)是一种直观法,其实质是观察交点坐标,即观察抛物线与x轴(即直线y=0)的交点.
经典例题
题型一
根据抛物线与直线的交点情况,求字母的取值(范围)
例1
已知关于x的二次函数y=(a-1)x2-2x+3的图象与坐标轴有两个交点,则a的值是____________.
题型一
根据抛物线与直线的交点情况,求字母的取值(范围)
题型一
根据抛物线与直线的交点情况,求字母的取值(范围)
方法归纳
根据二次函数的图象与直线y=m(m为常数)的交点情况,求有关字母的值或取值范围时,解题方法是根据对应的一元二次方程的根的情况,利用根的判别式列方程或不等式求解注意:若未说明函数是哪种类型的函数,还需分情况讨论.
题型二
根据二次函数的图象求解一元二次方程或不等式
例2
抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过A(2,0),B(-4,0)两点,下列四个结论:
①一元二次方程ax2+bx+c=0的根为x1=2,x2=-4;
②若点C(-5,y1),D(m,y2)在该抛物线上,则y1<y2;
③对于任意实数t,总有at2+bt≤a-b;
④对于a的每一个确定值,若一元二次方程ax2+bx+c=p(p为常数,p>0)的根为整数,则p的值只有两个.
其中正确的结论是___________(填写序号).
方法归纳
易错易混
易错点
考虑不周,忽略分类讨论
判断函数图象与坐标轴的交点,要考虑两种情况,一是若函数是一次函数,则函数图象与坐标轴必有交点;二是若函数是二次函数,要分与x轴相交、与y轴相交两种情况讨论抛物线与y轴必有一交点,与x轴的交点则由b2-4ac决定注意不要忽略抛物线与y轴必有交点的情况.
例
若函数y=mx2+x+1的图象与x轴只有一个公共点,则m的值是__________.
