1.1集合的含义与表示 课件(共30张PPT)
文档属性
| 名称 | 1.1集合的含义与表示 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 14:29:54 | ||
图片预览











文档简介
(共30张PPT)
数学
北师大必修1
1.1集合的含义与表示
一般地,指定的某些对象的全体称为集合(简称集).集合常用大写字母A,B,C,D,…标记.
集合中的每个对象叫作这个集合的元素.常用小写字母a,b,c,d,…表示集合中的元素.
例如:小于10的素数集合可以记为B,它的元素为2,3,5,7.
集合与元素的定义
给定一个集合A,任何一个对象α是不是这个集合的元素就确定了.
若a在集合A中,就说a属于集合A,记作a∈A;
若a不在集合A中,就说α不属于集合A,记作aA.
例如,小于10的素数集合可以记为B,它的元素为2,3,5,7.在上述素数问题中,2∈B,6B.
集合元素的确定性
又如本班所有高个子的同学,
“高个子的同学”对象不确定,因而不能组成集合.
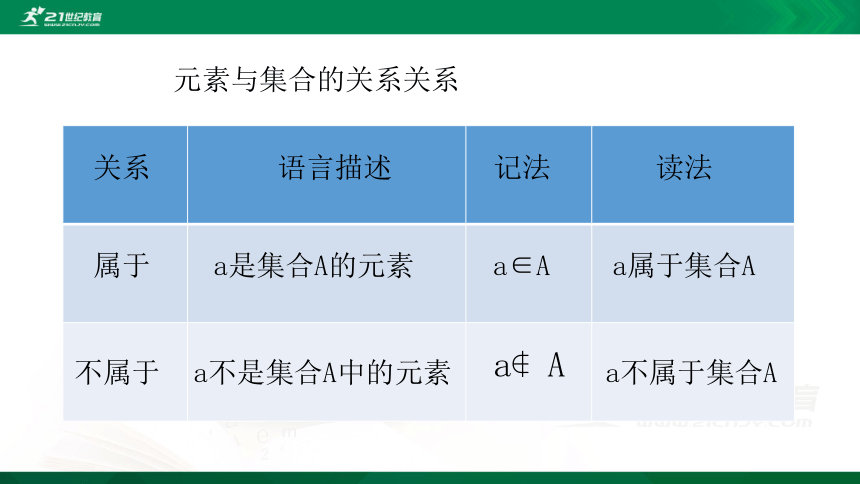
元素与集合的关系关系
语言描述
记法
关系
读法
属于
a是集合A的元素
a不是集合A中的元素
不属于
a∈A
a属于集合A
a不属于集合A
a?A
数的集合简称数集.下面是一些常用的数集及其记法:
自然数组成的集合简称自然数集,
正整数组成的集合简称正整数集,
整数组成的集合简称整数集,
有理数组成的集合简称有理数集,
实数组成的集合简称实数集,
例如,0∈N,
记作N;
记作N+或N
;
记作
Z;
记作Q;
记作R.
π∈R等
∈R,
0.618∈Q,
用符号“∈”或“
”
填空:(口答)
(1)
3.14_______Q
(2)
π_______Q
(3)
0_______N
(4)
0_______N+
(5)
(-0.5)0_______Z
(6)
2_______R
∈
∈
∈
∈
?
集合的常用表示法有列举法和描述法.
表示法
列举法是把集合中的元素一一列举出来写在大括号内的方法.符号表示为{,…,},各元素之间用逗号分隔.如{x1
,x2,…,xn}.
例如,在江苏省水面面积在1500
km2以上的天然湖组成的集合用列举法可以表示为C={太湖,洪泽湖}.
列举法
有时,我们无法将集合中的元素一一列举出来.将集合的所有元素都具有的性质P(满足的条件)表示出来,写成{x
|
p(x)}的形式。
如{x∈A|
p(x)}.
例如,大于3小于10的实数组成的集合,我们用{x∈R|3像这样,用确定的条件表示某些对象属于一个集合并写在大括号内的方法叫描述法.
若一个集合中的元素都是在实数范围内,如{x∈R|3描述法
符号表示为{|},
例如,不等式x—32>0的解集用描述法可以表示为
方程x2+2x=0的解集用描述法可以表示为
又如,在平面直角坐标系中第二象限的点构成的集合,用描述法可以表示为
C={(x,y)|x<0,且
y>0}.
函数y=2x图像上的点(x,y)的集合可以表示为
D={(x,y)|y=2x}.
A={x|x>32};
B={x|x2+2x=0}.
列举法和描述法是集合的常用表示方法.用什么方法表示集合,要具体问题具体分析.
用描述法表示集合时注意:
(1)弄清元素所具有的形式(即代表元素是什么),是数、还是有序实数对(点)等.
(2)元素具有怎样的属性?
用描述法表示集合时,若需要多层次描述属性时,可选用联结词“且”与“或”等联结;若描述部分出现元素记号以外的字母时,要对新字母说明其含义或指出其取值范围.
在给定的集合中,元素是互异的.也就是说,集合中的任何两个元素都不相同,因此,集合中的元素没有重复现象.
集合元素的互异性
例1用列举法表示下列集合:
(1)由大于3小于10的整数组成的集合;
(2)方程x2一9=0的解的集合.
解(1)由大于3小于10的整数组成的集合用列举法可表示为{4,5,6,7,8,9};
(2)方程x2一9=0的解的集合用列举法可表示为{3,3}.
例2用描述法表示下列集合:
(1)小于10的所有有理数组成的集合;
(2)所有偶数组成的集合.
解(1)小于10的所有有理数组成的集合用描述法可表示为{x∈Q|x<10};
(2)偶数是能被2整除的数,可以写成x=2n(n∈Z)的形式,因此,偶数的集合用描述法可表示为{x|x=2n,n∈Z}.
所有偶数组成的集合也可以表示为{x|
∈Z}
一般地,我们把含有限个元素的集合叫有限集,如集合A={—2,3};
含无限个元素的集合叫无限集,如整数的集合Z.
我们再看一个例子,由于方程x2十2=0在实数集R内无解,因此,它的实数解组成的集合{x∈R|x2+2=0}中没有任何元素.
我们把不含有任何元素的集合叫作空集,
如集合{x∈R|x2+2=0}就是空集.
记作?,
集合中的元素是无先后顺序的,即集合里的任何两个元素可以交换位置。如由1,2,3和3,2,1构成的集合是同一个集合.
集合元素的无序性
小结:集合元素的三大特点:无序性,确定性,互异性
(3)和2003非常接近的数;
(4)方程x2+1=0的实数解;
(5)满足x-2<8的全体实数。
[例1]
下面各组对象能否构成集合?
(1)所有的好人;
(2)小于2003的数;
×
×
[例1]“book”中的字母构成一个集合,该集合的元素是
b,o,k三个字母
【例2】若一个集合中的三个元素a,b,c是△ABC的三边长,则此三角形一定不是(
)
(A)锐角三角形
(B)直角三角形
(C)钝角三角形
(D)等腰三角形
【审题指导】欲判断三角形的形状,需判断三边关系或三角关系.由于已知条件涉及三边,故考虑三边之间的关系.
【规范解答】选D.由于集合中元素具有互异性,即a,b,c互不相等,因此△ABC一定不是等腰三角形.
练习2:下列说法中正确的是(
)
A、2004年雅典奥运会的所有比赛项目组成一个集合
B、某个班年龄较小的学生组成一个集合
C、1、2、3组成的集合与2、1、3组成的集合是不同的
两个集合
D、{1,2,2,3}是含1个1,2个2,1个3的四个元素的集合
练习3、下列给出的对象中,能表示集合的是(
)
A、一切很大的数;
B、无限接近0的数;
C、聪明的人;
D、方程x2=2的实数根。
A
D
练习4若集合{-1,|x|}与{x,x2}相等,求实数x的值.
[解析] ∵{-1,|x|}与{x,x2}两集合相等,∴两集合含有相同的元素
即{x,x2}一定含有-1这个元素
由于x2≥0,∴x=-1.
[解] ∵1∈A,∴a+2,(a+1)2,a2+3a+3都可能等于1.
①若a+2=1,则a=-1,此时A中的元素为1,0,1与集合中元素的互异性矛盾,故舍去;
②若(a+1)2=1,则a=0或a=-2,
当a=0时,A={2,1,3}适合题意,
当a=-2时,A中的元素为0,1,1与集合中元素的互异性矛盾,舍去,
③若a2+3a+3=1,则a=-1或a=-2,由①②知都不合题意,舍去.
综上所述,a=0.
例
已知集合A={a+2,(a+1)2,a2+3a+3},若1∈A,求实数a的值.
A={0,6,8}
B={1,3,9}
C={2,5,6}
D={(0,6),(1,5),(2,2)}
E={0,
,4}
【即时训练】若集合M中含有三个元素-2,3x2+3x-4,
x2+x-4,且2∈M,求x的值.
【解析】由条件分两种情况讨论:
(1)当3x2+3x-4=2时,
3x2+3x-6=0,x2+x-2=0,
∴x=-2或x=1,此时x2+x-4=-2,M中只有二个元素-2和2,不符合题意
(2)当x2+x-4=2时,
x2+x-6=0,∴x=-3或x=2,
经检验x=-3,x=2均符合题意.
综上可知x=-3或x=2.
本节小结:
集合与元素的定义
集合的常用表示法有列举法和描述法.
集合元素的互异性
集合元素的确定性
集合元素的无序性
元素与集合的关系是属于或不属于的关系
扩展备用:集合的表示方法
(1)字母表示法;
(2)自然语言法;
(3)列举法;
(4)描述法;
(5)韦恩(Venn)图;
(6)区间法。
作业2 集合A={x|x=3n+1,n∈Z},B={x|x=3n+2,n∈Z},C={x|x=6n+3,n∈Z},对任意的a∈A,b∈B,是否一定有a+b∈C?并证明你的结论.
[正解] 设a=3m+1(m∈Z),b=3t+2(t∈Z),
则a+b=3(m+t)+3,
当m+t是偶数时,设m+t=2k(k∈Z),
有a+b=6k+3(k∈Z),则a+b∈C;
当m+t为奇数时,设m+t=2k-1(k∈Z),
有a+b=6k(k∈Z),则a+b?C
综上可知不一定有a+b∈C.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学
北师大必修1
1.1集合的含义与表示
一般地,指定的某些对象的全体称为集合(简称集).集合常用大写字母A,B,C,D,…标记.
集合中的每个对象叫作这个集合的元素.常用小写字母a,b,c,d,…表示集合中的元素.
例如:小于10的素数集合可以记为B,它的元素为2,3,5,7.
集合与元素的定义
给定一个集合A,任何一个对象α是不是这个集合的元素就确定了.
若a在集合A中,就说a属于集合A,记作a∈A;
若a不在集合A中,就说α不属于集合A,记作aA.
例如,小于10的素数集合可以记为B,它的元素为2,3,5,7.在上述素数问题中,2∈B,6B.
集合元素的确定性
又如本班所有高个子的同学,
“高个子的同学”对象不确定,因而不能组成集合.
元素与集合的关系关系
语言描述
记法
关系
读法
属于
a是集合A的元素
a不是集合A中的元素
不属于
a∈A
a属于集合A
a不属于集合A
a?A
数的集合简称数集.下面是一些常用的数集及其记法:
自然数组成的集合简称自然数集,
正整数组成的集合简称正整数集,
整数组成的集合简称整数集,
有理数组成的集合简称有理数集,
实数组成的集合简称实数集,
例如,0∈N,
记作N;
记作N+或N
;
记作
Z;
记作Q;
记作R.
π∈R等
∈R,
0.618∈Q,
用符号“∈”或“
”
填空:(口答)
(1)
3.14_______Q
(2)
π_______Q
(3)
0_______N
(4)
0_______N+
(5)
(-0.5)0_______Z
(6)
2_______R
∈
∈
∈
∈
?
集合的常用表示法有列举法和描述法.
表示法
列举法是把集合中的元素一一列举出来写在大括号内的方法.符号表示为{,…,},各元素之间用逗号分隔.如{x1
,x2,…,xn}.
例如,在江苏省水面面积在1500
km2以上的天然湖组成的集合用列举法可以表示为C={太湖,洪泽湖}.
列举法
有时,我们无法将集合中的元素一一列举出来.将集合的所有元素都具有的性质P(满足的条件)表示出来,写成{x
|
p(x)}的形式。
如{x∈A|
p(x)}.
例如,大于3小于10的实数组成的集合,我们用{x∈R|3
若一个集合中的元素都是在实数范围内,如{x∈R|3
符号表示为{|},
例如,不等式x—32>0的解集用描述法可以表示为
方程x2+2x=0的解集用描述法可以表示为
又如,在平面直角坐标系中第二象限的点构成的集合,用描述法可以表示为
C={(x,y)|x<0,且
y>0}.
函数y=2x图像上的点(x,y)的集合可以表示为
D={(x,y)|y=2x}.
A={x|x>32};
B={x|x2+2x=0}.
列举法和描述法是集合的常用表示方法.用什么方法表示集合,要具体问题具体分析.
用描述法表示集合时注意:
(1)弄清元素所具有的形式(即代表元素是什么),是数、还是有序实数对(点)等.
(2)元素具有怎样的属性?
用描述法表示集合时,若需要多层次描述属性时,可选用联结词“且”与“或”等联结;若描述部分出现元素记号以外的字母时,要对新字母说明其含义或指出其取值范围.
在给定的集合中,元素是互异的.也就是说,集合中的任何两个元素都不相同,因此,集合中的元素没有重复现象.
集合元素的互异性
例1用列举法表示下列集合:
(1)由大于3小于10的整数组成的集合;
(2)方程x2一9=0的解的集合.
解(1)由大于3小于10的整数组成的集合用列举法可表示为{4,5,6,7,8,9};
(2)方程x2一9=0的解的集合用列举法可表示为{3,3}.
例2用描述法表示下列集合:
(1)小于10的所有有理数组成的集合;
(2)所有偶数组成的集合.
解(1)小于10的所有有理数组成的集合用描述法可表示为{x∈Q|x<10};
(2)偶数是能被2整除的数,可以写成x=2n(n∈Z)的形式,因此,偶数的集合用描述法可表示为{x|x=2n,n∈Z}.
所有偶数组成的集合也可以表示为{x|
∈Z}
一般地,我们把含有限个元素的集合叫有限集,如集合A={—2,3};
含无限个元素的集合叫无限集,如整数的集合Z.
我们再看一个例子,由于方程x2十2=0在实数集R内无解,因此,它的实数解组成的集合{x∈R|x2+2=0}中没有任何元素.
我们把不含有任何元素的集合叫作空集,
如集合{x∈R|x2+2=0}就是空集.
记作?,
集合中的元素是无先后顺序的,即集合里的任何两个元素可以交换位置。如由1,2,3和3,2,1构成的集合是同一个集合.
集合元素的无序性
小结:集合元素的三大特点:无序性,确定性,互异性
(3)和2003非常接近的数;
(4)方程x2+1=0的实数解;
(5)满足x-2<8的全体实数。
[例1]
下面各组对象能否构成集合?
(1)所有的好人;
(2)小于2003的数;
×
×
[例1]“book”中的字母构成一个集合,该集合的元素是
b,o,k三个字母
【例2】若一个集合中的三个元素a,b,c是△ABC的三边长,则此三角形一定不是(
)
(A)锐角三角形
(B)直角三角形
(C)钝角三角形
(D)等腰三角形
【审题指导】欲判断三角形的形状,需判断三边关系或三角关系.由于已知条件涉及三边,故考虑三边之间的关系.
【规范解答】选D.由于集合中元素具有互异性,即a,b,c互不相等,因此△ABC一定不是等腰三角形.
练习2:下列说法中正确的是(
)
A、2004年雅典奥运会的所有比赛项目组成一个集合
B、某个班年龄较小的学生组成一个集合
C、1、2、3组成的集合与2、1、3组成的集合是不同的
两个集合
D、{1,2,2,3}是含1个1,2个2,1个3的四个元素的集合
练习3、下列给出的对象中,能表示集合的是(
)
A、一切很大的数;
B、无限接近0的数;
C、聪明的人;
D、方程x2=2的实数根。
A
D
练习4若集合{-1,|x|}与{x,x2}相等,求实数x的值.
[解析] ∵{-1,|x|}与{x,x2}两集合相等,∴两集合含有相同的元素
即{x,x2}一定含有-1这个元素
由于x2≥0,∴x=-1.
[解] ∵1∈A,∴a+2,(a+1)2,a2+3a+3都可能等于1.
①若a+2=1,则a=-1,此时A中的元素为1,0,1与集合中元素的互异性矛盾,故舍去;
②若(a+1)2=1,则a=0或a=-2,
当a=0时,A={2,1,3}适合题意,
当a=-2时,A中的元素为0,1,1与集合中元素的互异性矛盾,舍去,
③若a2+3a+3=1,则a=-1或a=-2,由①②知都不合题意,舍去.
综上所述,a=0.
例
已知集合A={a+2,(a+1)2,a2+3a+3},若1∈A,求实数a的值.
A={0,6,8}
B={1,3,9}
C={2,5,6}
D={(0,6),(1,5),(2,2)}
E={0,
,4}
【即时训练】若集合M中含有三个元素-2,3x2+3x-4,
x2+x-4,且2∈M,求x的值.
【解析】由条件分两种情况讨论:
(1)当3x2+3x-4=2时,
3x2+3x-6=0,x2+x-2=0,
∴x=-2或x=1,此时x2+x-4=-2,M中只有二个元素-2和2,不符合题意
(2)当x2+x-4=2时,
x2+x-6=0,∴x=-3或x=2,
经检验x=-3,x=2均符合题意.
综上可知x=-3或x=2.
本节小结:
集合与元素的定义
集合的常用表示法有列举法和描述法.
集合元素的互异性
集合元素的确定性
集合元素的无序性
元素与集合的关系是属于或不属于的关系
扩展备用:集合的表示方法
(1)字母表示法;
(2)自然语言法;
(3)列举法;
(4)描述法;
(5)韦恩(Venn)图;
(6)区间法。
作业2 集合A={x|x=3n+1,n∈Z},B={x|x=3n+2,n∈Z},C={x|x=6n+3,n∈Z},对任意的a∈A,b∈B,是否一定有a+b∈C?并证明你的结论.
[正解] 设a=3m+1(m∈Z),b=3t+2(t∈Z),
则a+b=3(m+t)+3,
当m+t是偶数时,设m+t=2k(k∈Z),
有a+b=6k+3(k∈Z),则a+b∈C;
当m+t为奇数时,设m+t=2k-1(k∈Z),
有a+b=6k(k∈Z),则a+b?C
综上可知不一定有a+b∈C.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
