1.2集合间的基本关系 课件(共23张PPT)
文档属性
| 名称 | 1.2集合间的基本关系 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
北师大必修1
1.2 集合间的基本关系
我们考察下面三个实例:
1.高一(1)班50位同学组成集合B,其中女同学组成集合A.集合A是集合B的一部分,
2.所有的矩形都是平行四边形.若用M表示矩形组成的集合,用P表示平行四边形组成的集合,
3.所有的有理数都是实数.因此有:
因此有:若a∈A,则a∈B.
则有:若a∈M,则a∈P.
若a∈Q,则a∈R.
一般地,对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素,即若a∈A,则a∈B,
我们就说集合A包含于集合B,记作A?B
或集合B包含集合A,记作B?A,
这时我们说集合A是集合B的子集.
比如,上面实例2就是M?P.
显然,任何一个集合都是它本身的子集,即A?A.
子集的定义
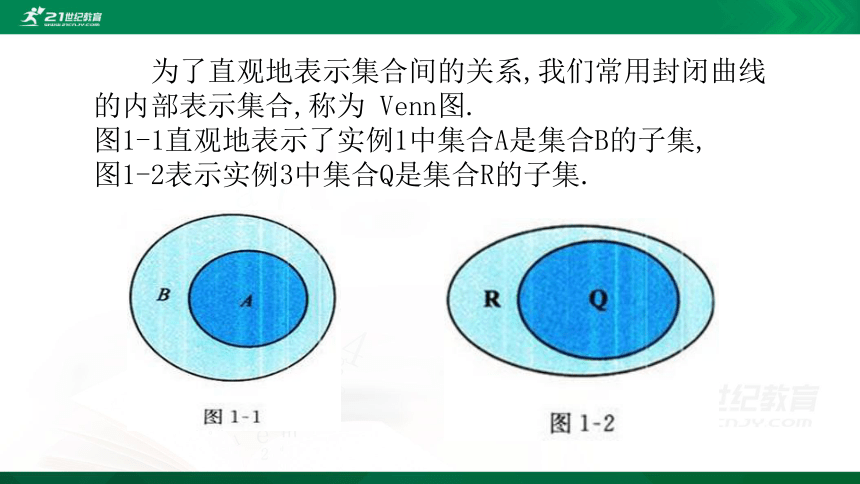
为了直观地表示集合间的关系,我们常用封闭曲线的内部表示集合,称为
Venn图.
图1-1直观地表示了实例1中集合A是集合B的子集,
图1-2表示实例3中集合Q是集合R的子集.
对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素,同时集合B中的任何一个元素都是集合A中的元素,这时,我们就说集合A与集合B相等(如图),
记作A=B.
例如,A={x
|(x—7)(x+5)=0},B={一5,7},不难看出,
A=B.
等集
即对于两个集合A与B,若A?B,且B?A,则A=B.
对于两个集合A与B,如果A?B,并且A≠B,
我们就说集合A是集合B的真子集(如图),
记作A
B(或B
A).
真子集
读作“A真包含于B”(或“B真包含A”).
例如,{a,b}
{a,b,c};
{x
|x-2}
{x
|x3}
·
·
·
-2
3
0
N+
N
Z
Q
R.
当集合A不包含于集合B,或集合B不包含集合A时,
记作A
B(或B
A).
例如,集合A={1,3,5},集合B={2,4,6},
则A
B(如图1-5);
集合A={1,3,5},集合B={5,7,9},
则A
B(如图1-6).
读作A不包含于集合B
(B不包含集合A)
又如,集合{x|x≥9}与集合{X|X≤3}的关系,可以表示为{x|x≥9}
{X|X≤3}(如图1-7);
数集的表示常借助于数轴.
又如,集合{x|x≥9}与集合{X|X≤12}的关系,
可以表示为{x|x≥9}
{X|X≤12}(如图1-8);
我们规定:空集是任何集合的子集.也就是说,对于任何一个集合A,都有
??A
例1某工厂生产的产品在质量和长度上都合格时,该产品才合格.若用A表示合格产品的集合,B表示质量合格的产品的集合,C表示长度合格的产品的集合,则下列包含关系哪些成立?A?B,B?A,A?C,C?A.试用Venn图表示这三个集合的关系.
解:由题意知,A?B,A?C,成立,
Venn图表示如图1-9所示.
(1)集合A是集合B的真子集,即A是B的子集,并且B中至少存在一个元素
A的元素;
(2)子集包括真子集和相等两种情况;
(3)空集?是任何
集合的真子集;
不是
说明:
非空
说说子集和真子集的区别?
(4)对于集合A,B,C,如果A
B,B
C,那么A___C;
如果A
B,B?C,那么A___C;如果A?B,B
C,那么A___C
易混符号
①“?”与“?”:
“?”元素与集合之间是属于关系;
“?”集合与集合之间是包含关系。
如:1
?
N,—1?N,Φ
?
R,{1}
?{1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,
Φ是不含任何元素的集合。
如:Φ
?
{0}。不能写成Φ={0},Φ∈{0}
但Φ?
{Φ}这个是对的,此时的Φ是一个元素
a与{a}的区别
一般地,a表示一个元素,而{a}表示只有一个元素a的集合,因此有
(3)空集是集合中的特殊现象,A?B包括A=?的情形容易漏掉,解题时要特别留意.(空集优先)
不能把“A?B”理解为“A是B中部分元素组成的集合”,因为当A=?时,A?B,但A中不含任何元素;又当A=B时,也有A?B,但A中含有B中所有元素,这两种情况都有A?B.
{a}?{a,b,c}.
a∈{a,b,c},
{1}?{1,2,3},
1∈{1,2,3},0∈{0},
例2写出集合{0,1,2}的所有子集,并指出其中哪些是它的真子集.
解{0,1,2}的所有子集是:
?;{0},{1},{2};{0,1},{0,2},{1,2};{0,1,2}.除了{0,1,2}以外,其余7个集合都是它的真子集.
小结:一个集合有n个元素,那么这个集合有2n个子集,
有2n-1个真子集(别忘记了空集)
非空真子集数为2n-2
练习:1.下列各组集合M与N中,表示相等集合的是(
)
A.M={(0,1)},N={0,1}
B.M={(0,1)},N={(1,0)}
C.M={(0,1)},N={(x,y)|x=0且y=1}
D.M={π},N={3.14}
【解析】C.对A,由于集合M是点集,集合N是数集,故M和N不相等;对B,虽然都是点集,但元素表示不同的点,故M和N不相等;对D,由于π是无理数,3.14是有理数,故M和N不相等.
C
2.同时满足:
①M?{1,2,3,4,5},②若a∈M,则6-a∈M的非空集合M有(
)
A.16个
B.15个
C.7个
D.6个
【解析】选C.∵1+5=2+4=3+3=6,∴集合M可能为单元素集合:{3};二元素集合:{1,5},{2,4};三元素集合:{1,3,5},
{2,3,4},四元素集合:{1,2,4,5},五元素集合:{1,2,3,4,5},共7个.
C
3.已知集合A={x|a<x<5},B={x|x≥2},且满足A?B,求实数a的取值范围.
解
①当a≥5时,A=?,此时有A?B;
②当a<5时,要使A?B,如图,需a≥2,所以2≤a<5.
综上,a的取值范围为a≥2.
例:已知集合A={x|1集合A中含有参数a
,在化简A时注意讨论.出现集合间的包含关系时应注意考虑集合是否是空集.
【规范解答】(1)当a=0时,A=?,满足条件
(2)当a≠0时,分两种情况:
①a>0时,A={x|
},B={x|-1∵A?B,且a>0,∴
∴a≥2.
②当a<0时,A={x|
}B={x|-1∵A?B,∴
综上可知,a≤-2或a=0或a≥2.
∴a≤-2.
本课小结
子集的定义
等集
真子集
1.已知集合A={x|x<-1或x>4},
B={x|2a≤x≤a+3},若B?A,求实数a的取值范围.
[解]
当B=?时,只需2a>a+3,即a>3;
当B≠?时,根据题意作出如图所示的数轴,
可得
a+3<-1
a+3≥2a,
解得a<-4或2<a≤3.
综上可得,实数a的取值范围为a<-4或a>2.
或
2a>4
(a+3≥2a)
作业布置
2.设集合A={a|a=3n+2,n∈Z},集合B={b|b=3k-1,k∈Z}
证明:A=B.
解
①对任意a∈A,则a=3n+2=3(n+1)-1(n∈Z),
∵n∈Z,∴n+1∈Z,
②又对任意b∈B,则b=3k-1=3(k-1)+2(k∈Z),
∵k∈Z,∴k-1∈Z,
∴b∈A,故B?A
由①、②知,A=B.
∴a∈B,故A?B
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大必修1
1.2 集合间的基本关系
我们考察下面三个实例:
1.高一(1)班50位同学组成集合B,其中女同学组成集合A.集合A是集合B的一部分,
2.所有的矩形都是平行四边形.若用M表示矩形组成的集合,用P表示平行四边形组成的集合,
3.所有的有理数都是实数.因此有:
因此有:若a∈A,则a∈B.
则有:若a∈M,则a∈P.
若a∈Q,则a∈R.
一般地,对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素,即若a∈A,则a∈B,
我们就说集合A包含于集合B,记作A?B
或集合B包含集合A,记作B?A,
这时我们说集合A是集合B的子集.
比如,上面实例2就是M?P.
显然,任何一个集合都是它本身的子集,即A?A.
子集的定义
为了直观地表示集合间的关系,我们常用封闭曲线的内部表示集合,称为
Venn图.
图1-1直观地表示了实例1中集合A是集合B的子集,
图1-2表示实例3中集合Q是集合R的子集.
对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素,同时集合B中的任何一个元素都是集合A中的元素,这时,我们就说集合A与集合B相等(如图),
记作A=B.
例如,A={x
|(x—7)(x+5)=0},B={一5,7},不难看出,
A=B.
等集
即对于两个集合A与B,若A?B,且B?A,则A=B.
对于两个集合A与B,如果A?B,并且A≠B,
我们就说集合A是集合B的真子集(如图),
记作A
B(或B
A).
真子集
读作“A真包含于B”(或“B真包含A”).
例如,{a,b}
{a,b,c};
{x
|x-2}
{x
|x3}
·
·
·
-2
3
0
N+
N
Z
Q
R.
当集合A不包含于集合B,或集合B不包含集合A时,
记作A
B(或B
A).
例如,集合A={1,3,5},集合B={2,4,6},
则A
B(如图1-5);
集合A={1,3,5},集合B={5,7,9},
则A
B(如图1-6).
读作A不包含于集合B
(B不包含集合A)
又如,集合{x|x≥9}与集合{X|X≤3}的关系,可以表示为{x|x≥9}
{X|X≤3}(如图1-7);
数集的表示常借助于数轴.
又如,集合{x|x≥9}与集合{X|X≤12}的关系,
可以表示为{x|x≥9}
{X|X≤12}(如图1-8);
我们规定:空集是任何集合的子集.也就是说,对于任何一个集合A,都有
??A
例1某工厂生产的产品在质量和长度上都合格时,该产品才合格.若用A表示合格产品的集合,B表示质量合格的产品的集合,C表示长度合格的产品的集合,则下列包含关系哪些成立?A?B,B?A,A?C,C?A.试用Venn图表示这三个集合的关系.
解:由题意知,A?B,A?C,成立,
Venn图表示如图1-9所示.
(1)集合A是集合B的真子集,即A是B的子集,并且B中至少存在一个元素
A的元素;
(2)子集包括真子集和相等两种情况;
(3)空集?是任何
集合的真子集;
不是
说明:
非空
说说子集和真子集的区别?
(4)对于集合A,B,C,如果A
B,B
C,那么A___C;
如果A
B,B?C,那么A___C;如果A?B,B
C,那么A___C
易混符号
①“?”与“?”:
“?”元素与集合之间是属于关系;
“?”集合与集合之间是包含关系。
如:1
?
N,—1?N,Φ
?
R,{1}
?{1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,
Φ是不含任何元素的集合。
如:Φ
?
{0}。不能写成Φ={0},Φ∈{0}
但Φ?
{Φ}这个是对的,此时的Φ是一个元素
a与{a}的区别
一般地,a表示一个元素,而{a}表示只有一个元素a的集合,因此有
(3)空集是集合中的特殊现象,A?B包括A=?的情形容易漏掉,解题时要特别留意.(空集优先)
不能把“A?B”理解为“A是B中部分元素组成的集合”,因为当A=?时,A?B,但A中不含任何元素;又当A=B时,也有A?B,但A中含有B中所有元素,这两种情况都有A?B.
{a}?{a,b,c}.
a∈{a,b,c},
{1}?{1,2,3},
1∈{1,2,3},0∈{0},
例2写出集合{0,1,2}的所有子集,并指出其中哪些是它的真子集.
解{0,1,2}的所有子集是:
?;{0},{1},{2};{0,1},{0,2},{1,2};{0,1,2}.除了{0,1,2}以外,其余7个集合都是它的真子集.
小结:一个集合有n个元素,那么这个集合有2n个子集,
有2n-1个真子集(别忘记了空集)
非空真子集数为2n-2
练习:1.下列各组集合M与N中,表示相等集合的是(
)
A.M={(0,1)},N={0,1}
B.M={(0,1)},N={(1,0)}
C.M={(0,1)},N={(x,y)|x=0且y=1}
D.M={π},N={3.14}
【解析】C.对A,由于集合M是点集,集合N是数集,故M和N不相等;对B,虽然都是点集,但元素表示不同的点,故M和N不相等;对D,由于π是无理数,3.14是有理数,故M和N不相等.
C
2.同时满足:
①M?{1,2,3,4,5},②若a∈M,则6-a∈M的非空集合M有(
)
A.16个
B.15个
C.7个
D.6个
【解析】选C.∵1+5=2+4=3+3=6,∴集合M可能为单元素集合:{3};二元素集合:{1,5},{2,4};三元素集合:{1,3,5},
{2,3,4},四元素集合:{1,2,4,5},五元素集合:{1,2,3,4,5},共7个.
C
3.已知集合A={x|a<x<5},B={x|x≥2},且满足A?B,求实数a的取值范围.
解
①当a≥5时,A=?,此时有A?B;
②当a<5时,要使A?B,如图,需a≥2,所以2≤a<5.
综上,a的取值范围为a≥2.
例:已知集合A={x|1
,在化简A时注意讨论.出现集合间的包含关系时应注意考虑集合是否是空集.
【规范解答】(1)当a=0时,A=?,满足条件
(2)当a≠0时,分两种情况:
①a>0时,A={x|
∴a≥2.
②当a<0时,A={x|
综上可知,a≤-2或a=0或a≥2.
∴a≤-2.
本课小结
子集的定义
等集
真子集
1.已知集合A={x|x<-1或x>4},
B={x|2a≤x≤a+3},若B?A,求实数a的取值范围.
[解]
当B=?时,只需2a>a+3,即a>3;
当B≠?时,根据题意作出如图所示的数轴,
可得
a+3<-1
a+3≥2a,
解得a<-4或2<a≤3.
综上可得,实数a的取值范围为a<-4或a>2.
或
2a>4
(a+3≥2a)
作业布置
2.设集合A={a|a=3n+2,n∈Z},集合B={b|b=3k-1,k∈Z}
证明:A=B.
解
①对任意a∈A,则a=3n+2=3(n+1)-1(n∈Z),
∵n∈Z,∴n+1∈Z,
②又对任意b∈B,则b=3k-1=3(k-1)+2(k∈Z),
∵k∈Z,∴k-1∈Z,
∴b∈A,故B?A
由①、②知,A=B.
∴a∈B,故A?B
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
