2021-2022学年人教五四新版六年级上册数学《第5章 圆柱与圆锥》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年人教五四新版六年级上册数学《第5章 圆柱与圆锥》单元测试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 179.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 21:27:56 | ||
图片预览




文档简介
2021-2022学年人教五四新版六年级上册数学《第5章
圆柱与圆锥》单元测试卷
一.选择题
1.德鑫轧钢厂要把一种底面直径6厘米,长1米的圆柱形钢锭,轧制成长4.5米,外径3厘米的无缝钢管,如果不计加工过程中的损耗,则这种无缝钢管的内径是( )
A.0.25厘米
B.2厘米
C.1厘米
D.0.5厘米
2.已知圆柱的底面半径为4,高为6,则这个圆柱的侧面积为( )
A.24
B.24π
C.48
D.48π
3.如图,圆锥底面半径为8,母线长15,则这个圆锥侧面展开图的扇形的圆心角∠α为( )
A.120°
B.150°
C.192°
D.2100
4.已知圆锥的母线长为5cm,底面半径为3cm,则此圆锥的侧面积为( )
A.12πcm2
B.15πcm2
C.20πcm2
D.30πcm2
5.如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )
A.3.6
B.1.8
C.3
D.6
6.有一圆柱形储油罐,其底面直径与高相等.现要在储油罐的表面均匀涂上一层油漆(不计损耗),则两个底面所需油漆量与侧面所需油漆量之比是( )
A.1:1
B.2:1
C.1:2
D.1:4
7.边长为4的正方形绕一条边旋转一周,所得几何体的侧面积等于( )
A.16
B.16π
C.32π
D.64π
8.如图,矩形ABCD的边长AB=1,BC=2.把BC绕B逆时针旋转,使C恰好落在AD上的点E处,线段BC扫过部分为扇形BCE.若扇形BCE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A.
B.
C.
D.
9.如图,圆锥的底面半径为6,母线长为10,则圆锥的侧面积是( )
A.36π
B.60π
C.96π
D.100π
10.一个圆柱的高为10cm,底面积为25πcm2,这个圆柱的表面积为( )
A.250πcm2
B.200πcm2
C.150πcm2
D.100πcm2
二.填空题
11.圆柱的底面周长为2π,高为3,则圆柱侧面展开图的面积是
.
12.已知圆锥的侧面积展开图面积是30π,母线长为10,则圆锥的底面圆半径等于
.
13.现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为
.
14.如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是
元(结果保留π).
15.一个高为15cm的圆柱形笔筒,底面圆的半径为5cm,那么它的侧面积为
cm2(结果保留π).
16.农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房(如图所示),则需塑料布y(m2)与半径R(m)的函数关系式是(不考虑塑料埋在土里的部分)
.
17.若圆锥的底面半径为3cm,母线长为4cm,则圆锥的侧面积为
cm2.(结果保留π)
18.现有一个边长为4cm的正方形,绕它的一边旋转一周,得到的几何体体积是
cm3.(结果用含π的式子表示)
19.有一底面半径为6cm,高为8cm的圆柱体易拉罐,其表面积为
cm2(结果保留π).
20.若一个圆锥的侧面展开图是一个半径为3cm,圆心角为120°的扇形,则该圆锥的侧面面积为
cm2(结果保留π).
三.解答题
21.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
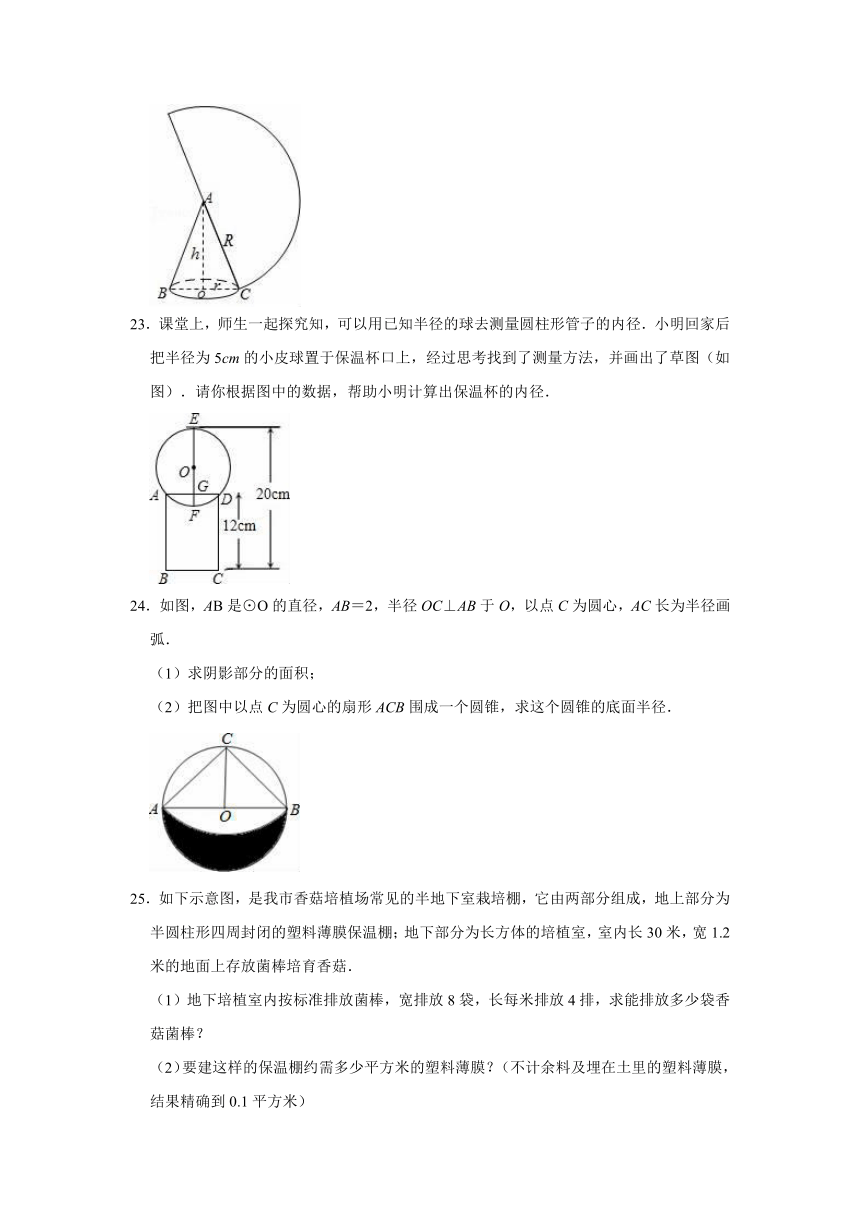
22.如图,一个圆锥的高为cm,侧面展开图是半圆,求:
(1)圆锥的底面半径r与母线R之比;
(2)圆锥的全面积.
23.课堂上,师生一起探究知,可以用已知半径的球去测量圆柱形管子的内径.小明回家后把半径为5cm的小皮球置于保温杯口上,经过思考找到了测量方法,并画出了草图(如图).请你根据图中的数据,帮助小明计算出保温杯的内径.
24.如图,AB是⊙O的直径,AB=2,半径OC⊥AB于O,以点C为圆心,AC长为半径画弧.
(1)求阴影部分的面积;
(2)把图中以点C为圆心的扇形ACB围成一个圆锥,求这个圆锥的底面半径.
25.如下示意图,是我市香菇培植场常见的半地下室栽培棚,它由两部分组成,地上部分为半圆柱形四周封闭的塑料薄膜保温棚;地下部分为长方体的培植室,室内长30米,宽1.2米的地面上存放菌棒培育香菇.
(1)地下培植室内按标准排放菌棒,宽排放8袋,长每米排放4排,求能排放多少袋香菇菌棒?
(2)要建这样的保温棚约需多少平方米的塑料薄膜?(不计余料及埋在土里的塑料薄膜,结果精确到0.1平方米)
26.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?(结果保留π)
参考答案与试题解析
一.选择题
1.解:设半径为xcm,
则:π××100=π×1.52×450﹣π×x2×450,
解得:x=0.5,
则内径=0.5×2=1cm
故选:C.
2.解:圆柱的侧面面积=π×4×2×6=48π.
故选:D.
3.解:圆锥底面周长=2×8π=16π,
∴扇形的圆心角α的度数=圆锥底面周长×180÷15π=192°.
故选:C.
4.解:底面周长是:2×3π=6π,
则圆锥的侧面积是:×6π×5=15πcm2.
故选:B.
5.解:设这个圆锥的底面半径为r,
根据题意得2πr=,
解得r=3.6,
即这个圆锥的底面半径是3.6.
故选:A.
6.解:两个底面的面积=π××2,侧面积=d×πd,所以是1:2,故选C.
7.解:边长为4的正方形绕一条边旋转一周,所得几何体是圆柱体,根据圆柱的侧面积公式可得π×4×2×4=32π,故选C.
8.解:∵线段CE由线段BC旋转而成,BC=2,
∴BE=BC=2.
∵AB=1,∠BAE=90°,
∴∠AEB=30°.
∵AD∥BC,
∴∠EBC=∠AEB=30°,
∴S阴影==,
设围成的圆锥的底面半径为r,则2πr=,
解得:r=.
故选:A.
9.解:底面周长是:2×6π=12π,
则圆锥的侧面积是:×12π×10=60π.
故选:B.
10.解:设底面半径为r,由题意知:πr2=25π,
解得:r=5cm,
则圆柱的侧面面积=2×π×5×10=100πcm2,
圆柱的全面积=25π×2+100π=150πcm2.
故选:C.
二.填空题
11.解:其侧面积为2π×3=6π.
12.解:设底面半径为R,则底面周长=2Rπ,圆锥的侧面展开图的面积=×2Rπ×10=30π,
∴R=3.
故答案为3.
13.解:20π=,解得:n=90°,
∵扇形纸片的圆心角是108°,
∴剪去的扇形纸片的圆心角为108°﹣90°=18°.
剪去的扇形纸片的圆心角为18°.
故答案为:18°.
14.解:根据题意得:圆锥侧面积=π×3×6=18π(平方米),
则购买油毡所需要的费用=10×18π=180π(元).
故答案为:180π.
15.解:它的侧面积为2π×5×15=150πcm2.
16.解:y=πR×30+πR2=30πR+πR2.
17.解:底面圆的半径为3,则底面周长=6π,侧面面积=×6π×4=12πcm2.
故答案为:12π.
18.解:根据圆柱体的计算公式:π×42×4=64πcm3.
故答案为64π.
19.解:π×6×2×8+π×36×2=168πcm2.
20.解:该圆锥的侧面面积==3π(cm2).
故答案为3π.
三.解答题
21.解:如图,由题意得:
2πr=,而r=2,
∴AB=6,
∴由勾股定理得:
AO2=AB2﹣OB2,而AB=6,OB=2,
∴AO=4.
即该圆锥的高为4.
22.解:(1)由题意可知
∴,R=2r(3分)r:R=r:2r=1:2;
(2)在Rt△AOC中,
∵R2=r2+h2
∴(5分),
4r2=r2+27r2=9,
r=±3
∵r>0
∴r=3,R=6(6分)
∴S侧=πRr=18π(cm2)(cm2)
∴S全=S侧+S底=18π+9π=27π(cm2).
23.解:连OD.
∵EG=20﹣12=8,
∴OG=8﹣5=3,
∴GD=4,
∴AD=2GD=8cm.
答:保温杯的内径为8cm.
24.解:(1)S阴=S△ABC+S半圆﹣S扇形CAB,
=AB?CO+﹣π
=1+﹣
=1
(2)设圆锥的半径为r,
∵S扇形ACB=πrl
∴=πr×
解得:r=
答:圆锥的半径为.
25.解:(1)宽排放8袋,长每米排放4排,共30米,所以培植室内能放8×4×30=960袋香菇菌棒;
(2)塑料棚的全面积为18π+0.36π=18.36π≈57.7.
∴要建这样的香菇保温棚需塑料薄膜57.7平方米.
26.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
圆柱与圆锥》单元测试卷
一.选择题
1.德鑫轧钢厂要把一种底面直径6厘米,长1米的圆柱形钢锭,轧制成长4.5米,外径3厘米的无缝钢管,如果不计加工过程中的损耗,则这种无缝钢管的内径是( )
A.0.25厘米
B.2厘米
C.1厘米
D.0.5厘米
2.已知圆柱的底面半径为4,高为6,则这个圆柱的侧面积为( )
A.24
B.24π
C.48
D.48π
3.如图,圆锥底面半径为8,母线长15,则这个圆锥侧面展开图的扇形的圆心角∠α为( )
A.120°
B.150°
C.192°
D.2100
4.已知圆锥的母线长为5cm,底面半径为3cm,则此圆锥的侧面积为( )
A.12πcm2
B.15πcm2
C.20πcm2
D.30πcm2
5.如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )
A.3.6
B.1.8
C.3
D.6
6.有一圆柱形储油罐,其底面直径与高相等.现要在储油罐的表面均匀涂上一层油漆(不计损耗),则两个底面所需油漆量与侧面所需油漆量之比是( )
A.1:1
B.2:1
C.1:2
D.1:4
7.边长为4的正方形绕一条边旋转一周,所得几何体的侧面积等于( )
A.16
B.16π
C.32π
D.64π
8.如图,矩形ABCD的边长AB=1,BC=2.把BC绕B逆时针旋转,使C恰好落在AD上的点E处,线段BC扫过部分为扇形BCE.若扇形BCE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A.
B.
C.
D.
9.如图,圆锥的底面半径为6,母线长为10,则圆锥的侧面积是( )
A.36π
B.60π
C.96π
D.100π
10.一个圆柱的高为10cm,底面积为25πcm2,这个圆柱的表面积为( )
A.250πcm2
B.200πcm2
C.150πcm2
D.100πcm2
二.填空题
11.圆柱的底面周长为2π,高为3,则圆柱侧面展开图的面积是
.
12.已知圆锥的侧面积展开图面积是30π,母线长为10,则圆锥的底面圆半径等于
.
13.现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为
.
14.如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是
元(结果保留π).
15.一个高为15cm的圆柱形笔筒,底面圆的半径为5cm,那么它的侧面积为
cm2(结果保留π).
16.农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房(如图所示),则需塑料布y(m2)与半径R(m)的函数关系式是(不考虑塑料埋在土里的部分)
.
17.若圆锥的底面半径为3cm,母线长为4cm,则圆锥的侧面积为
cm2.(结果保留π)
18.现有一个边长为4cm的正方形,绕它的一边旋转一周,得到的几何体体积是
cm3.(结果用含π的式子表示)
19.有一底面半径为6cm,高为8cm的圆柱体易拉罐,其表面积为
cm2(结果保留π).
20.若一个圆锥的侧面展开图是一个半径为3cm,圆心角为120°的扇形,则该圆锥的侧面面积为
cm2(结果保留π).
三.解答题
21.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
22.如图,一个圆锥的高为cm,侧面展开图是半圆,求:
(1)圆锥的底面半径r与母线R之比;
(2)圆锥的全面积.
23.课堂上,师生一起探究知,可以用已知半径的球去测量圆柱形管子的内径.小明回家后把半径为5cm的小皮球置于保温杯口上,经过思考找到了测量方法,并画出了草图(如图).请你根据图中的数据,帮助小明计算出保温杯的内径.
24.如图,AB是⊙O的直径,AB=2,半径OC⊥AB于O,以点C为圆心,AC长为半径画弧.
(1)求阴影部分的面积;
(2)把图中以点C为圆心的扇形ACB围成一个圆锥,求这个圆锥的底面半径.
25.如下示意图,是我市香菇培植场常见的半地下室栽培棚,它由两部分组成,地上部分为半圆柱形四周封闭的塑料薄膜保温棚;地下部分为长方体的培植室,室内长30米,宽1.2米的地面上存放菌棒培育香菇.
(1)地下培植室内按标准排放菌棒,宽排放8袋,长每米排放4排,求能排放多少袋香菇菌棒?
(2)要建这样的保温棚约需多少平方米的塑料薄膜?(不计余料及埋在土里的塑料薄膜,结果精确到0.1平方米)
26.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?(结果保留π)
参考答案与试题解析
一.选择题
1.解:设半径为xcm,
则:π××100=π×1.52×450﹣π×x2×450,
解得:x=0.5,
则内径=0.5×2=1cm
故选:C.
2.解:圆柱的侧面面积=π×4×2×6=48π.
故选:D.
3.解:圆锥底面周长=2×8π=16π,
∴扇形的圆心角α的度数=圆锥底面周长×180÷15π=192°.
故选:C.
4.解:底面周长是:2×3π=6π,
则圆锥的侧面积是:×6π×5=15πcm2.
故选:B.
5.解:设这个圆锥的底面半径为r,
根据题意得2πr=,
解得r=3.6,
即这个圆锥的底面半径是3.6.
故选:A.
6.解:两个底面的面积=π××2,侧面积=d×πd,所以是1:2,故选C.
7.解:边长为4的正方形绕一条边旋转一周,所得几何体是圆柱体,根据圆柱的侧面积公式可得π×4×2×4=32π,故选C.
8.解:∵线段CE由线段BC旋转而成,BC=2,
∴BE=BC=2.
∵AB=1,∠BAE=90°,
∴∠AEB=30°.
∵AD∥BC,
∴∠EBC=∠AEB=30°,
∴S阴影==,
设围成的圆锥的底面半径为r,则2πr=,
解得:r=.
故选:A.
9.解:底面周长是:2×6π=12π,
则圆锥的侧面积是:×12π×10=60π.
故选:B.
10.解:设底面半径为r,由题意知:πr2=25π,
解得:r=5cm,
则圆柱的侧面面积=2×π×5×10=100πcm2,
圆柱的全面积=25π×2+100π=150πcm2.
故选:C.
二.填空题
11.解:其侧面积为2π×3=6π.
12.解:设底面半径为R,则底面周长=2Rπ,圆锥的侧面展开图的面积=×2Rπ×10=30π,
∴R=3.
故答案为3.
13.解:20π=,解得:n=90°,
∵扇形纸片的圆心角是108°,
∴剪去的扇形纸片的圆心角为108°﹣90°=18°.
剪去的扇形纸片的圆心角为18°.
故答案为:18°.
14.解:根据题意得:圆锥侧面积=π×3×6=18π(平方米),
则购买油毡所需要的费用=10×18π=180π(元).
故答案为:180π.
15.解:它的侧面积为2π×5×15=150πcm2.
16.解:y=πR×30+πR2=30πR+πR2.
17.解:底面圆的半径为3,则底面周长=6π,侧面面积=×6π×4=12πcm2.
故答案为:12π.
18.解:根据圆柱体的计算公式:π×42×4=64πcm3.
故答案为64π.
19.解:π×6×2×8+π×36×2=168πcm2.
20.解:该圆锥的侧面面积==3π(cm2).
故答案为3π.
三.解答题
21.解:如图,由题意得:
2πr=,而r=2,
∴AB=6,
∴由勾股定理得:
AO2=AB2﹣OB2,而AB=6,OB=2,
∴AO=4.
即该圆锥的高为4.
22.解:(1)由题意可知
∴,R=2r(3分)r:R=r:2r=1:2;
(2)在Rt△AOC中,
∵R2=r2+h2
∴(5分),
4r2=r2+27r2=9,
r=±3
∵r>0
∴r=3,R=6(6分)
∴S侧=πRr=18π(cm2)(cm2)
∴S全=S侧+S底=18π+9π=27π(cm2).
23.解:连OD.
∵EG=20﹣12=8,
∴OG=8﹣5=3,
∴GD=4,
∴AD=2GD=8cm.
答:保温杯的内径为8cm.
24.解:(1)S阴=S△ABC+S半圆﹣S扇形CAB,
=AB?CO+﹣π
=1+﹣
=1
(2)设圆锥的半径为r,
∵S扇形ACB=πrl
∴=πr×
解得:r=
答:圆锥的半径为.
25.解:(1)宽排放8袋,长每米排放4排,共30米,所以培植室内能放8×4×30=960袋香菇菌棒;
(2)塑料棚的全面积为18π+0.36π=18.36π≈57.7.
∴要建这样的香菇保温棚需塑料薄膜57.7平方米.
26.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
