2021-2022学年人教版数学七年级上册4.1.2 点、线、面、体 课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册4.1.2 点、线、面、体 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
第四章
几何图形
4.1
几何图形
4.1.2
点、线、面、体
图片引入
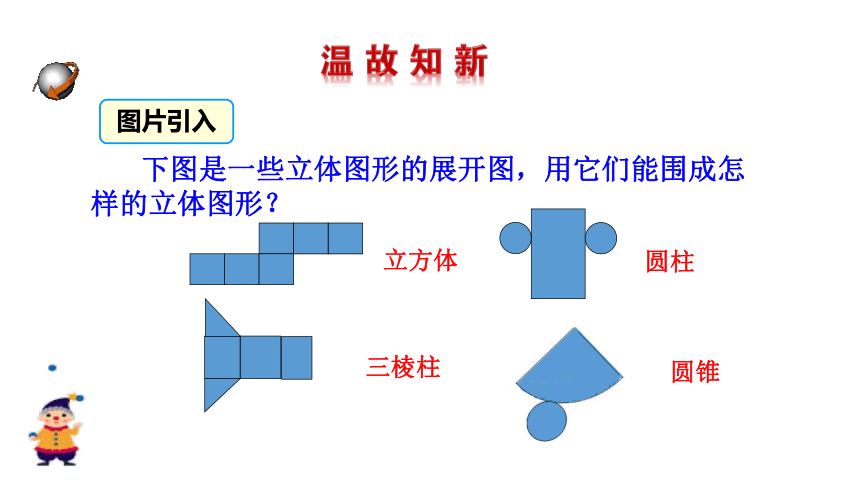
下图是一些立体图形的展开图,用它们能围成怎样的立体图形?
立方体
圆柱
三棱柱
圆锥
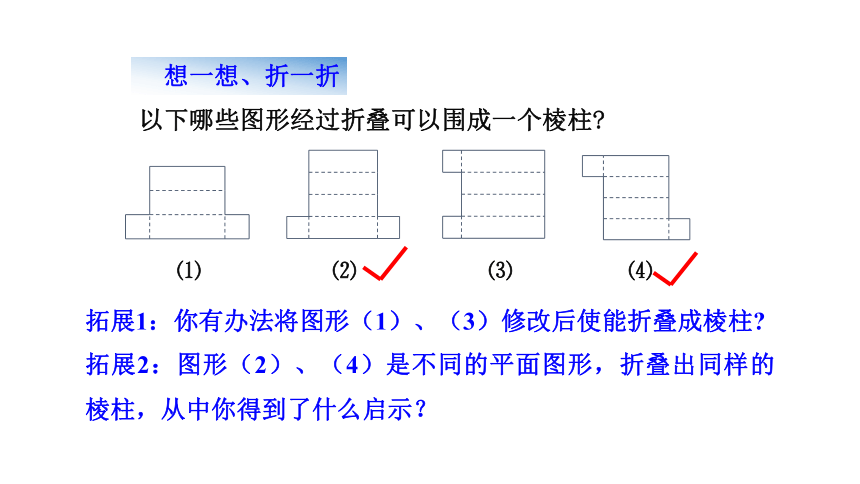
以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
拓展1:你有办法将图形(1)、(3)修改后使能折叠成棱柱?
拓展2:图形(2)、(4)是不同的平面图形,折叠出同样的棱柱,从中你得到了什么启示?
想一想、折一折
5
6
4
3
2
F
E
A
B
C
1
祝
你
前
程
似
锦
D
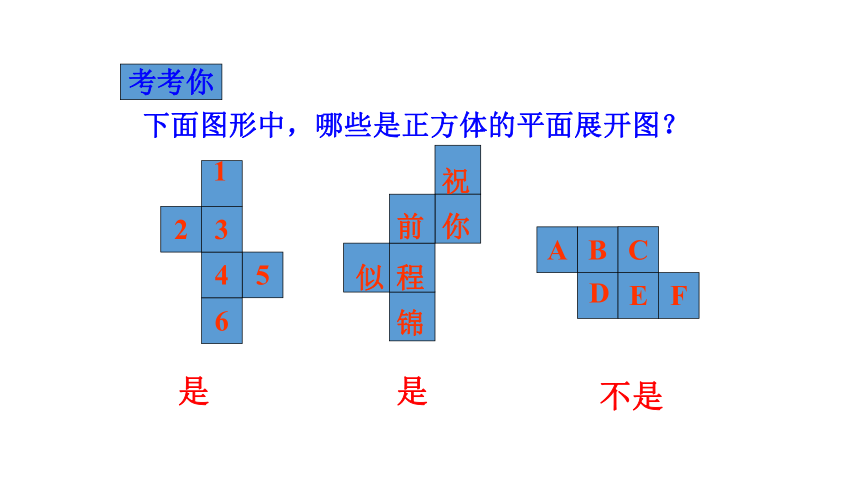
下面图形中,哪些是正方体的平面展开图?
考考你
是
是
不是
1.能结合几何模型或身边环境,指出体、面、线、点,并能区分平面和曲面、直线和曲线.
2.能从运动、集合的角度描述点、线、面、体的关系,并能恰当地举例来说明它们的关系.
3.初步体会“具体→抽象→具体”的认知方法.
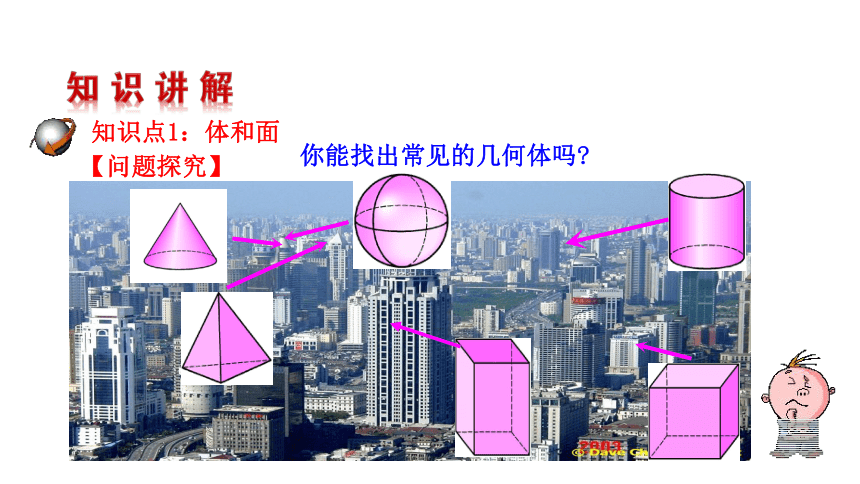
知识点1:体和面
【问题探究】
你能找出常见的几何体吗?
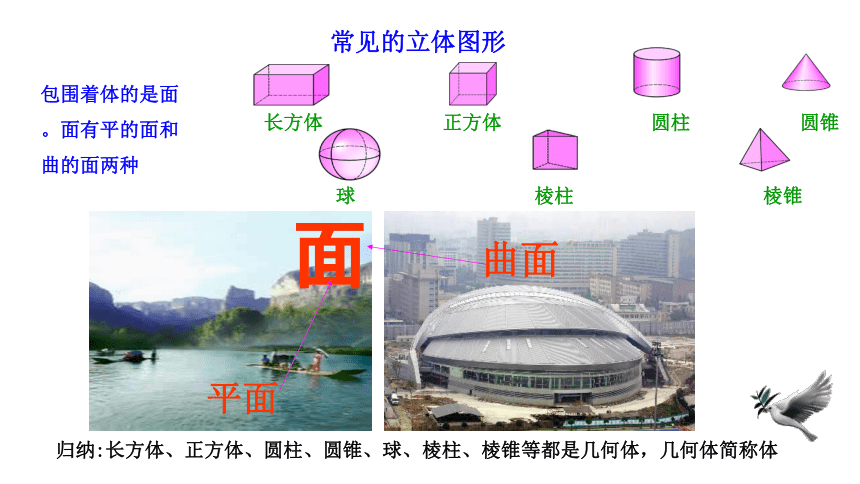
归纳:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体简称体
常见的立体图形
包围着体的是面。面有平的面和曲的面两种
长方体
正方体
圆柱
圆锥
球
棱柱
棱锥
面
平面
曲面
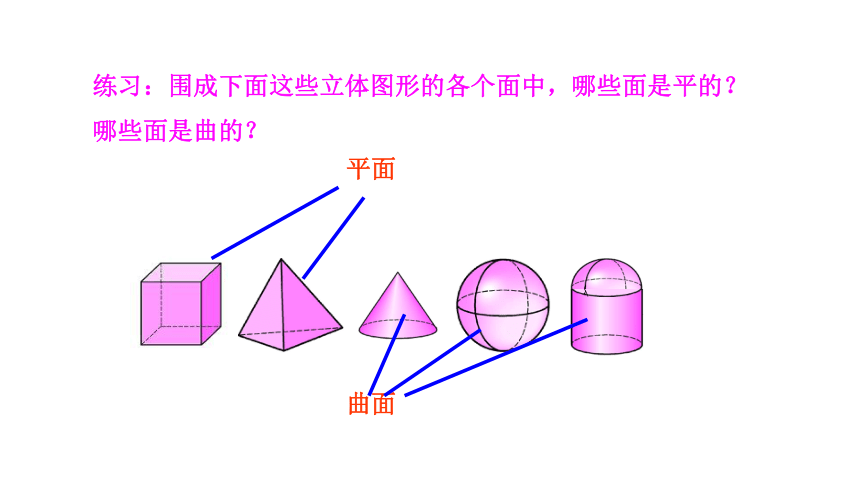
练习:围成下面这些立体图形的各个面中,哪些面是平的?哪些面是曲的?
平面
曲面
知识点2:线和点
【问题探究】
想一想,举出生活中符合线、点形象的例子.
线的形象
线:直线和曲线
点的形象
点
点是构成图形的基本元素
面与面相交的地方形成线
体会:
知识点3:点、线、面、体的关系
【问题探究1】
物体的运动会留下运动轨迹,这些运动轨迹往往也能抽象成几何图形.如果把笔尖看成一个点,这个点在纸上运动时,形成的图形是什么?动手试一试.
归纳结论:
点动成线.
点动成线.
?
例
点动成线
线动成面.
【问题探究2】
汽车的雨刷在挡风玻璃上画出一个扇面,从几何的角度观察这种现象,你可以得出什么结论?
线动成面.
概括结论:
例
线动成面
面动成体.
【问题探究3】
既然“点动成线,线动成面”,那么请同学们想一想:当面运动时又会形成什么图形?如何验证你的猜想?
概括结论:
面动成体.
例
三角形绕一边旋转成圆锥体
长方形绕一边旋转成圆柱体
如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,把有对应关系的平面图形与立体图形连接起来.
【跟踪训练】
连一连
归纳总结
归纳总结
点动成——
线动成——
面动成——
线
面
体
体是由面组成
面与面相交成线
线与线相交成点
判定几何体点、线、面的个数
【举一反三】
下图是一个长方体的模型,它有几个面?面和面相交的地方形成了几条线?线和线相交成几个点?
6个面
12条线
8个点
·
·
·
·
·
·
·
·
【思考交流】
旋转形成几何体的体积
在长方形ABCD中,AB=2,BC=3,把该图形沿着一边所在直线旋转一周,求所围成的几何体的体积.
解:分两种情况:
①当绕AB旋转时,则V=πBC2×AB=18π;
②当绕BC旋转时,则V=πAB2×BC=12π.
答:所围成的几何体的体积为18π或12π.
分析:矩形绕一边旋转后得到圆柱,根据圆柱的体积公式,分两种情况讨论可得出答案.
点、线、面的规律探究
【迁移应用】
如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有_____个面,______条棱,______个顶点;
(2)六棱柱有_____个面,______条棱,______个顶点;
(3)由此猜想n棱柱有_____个面,______条棱,_______个顶点.
(4)你发现棱柱的面数、棱数与顶点数之间存在怎样的数量关系?
分析:结合三棱柱、四棱柱、五棱柱和六棱柱的特点,可知n棱柱面、棱和顶点的个数.
解:四棱柱有6个面,12条棱,8个顶点;
六棱柱有8个面,18条棱,12个顶点;
由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
答:因为(n+2)+2n-3n=2,
所以发现棱柱的面数﹢顶点数﹣棱数﹦2.
1、多姿多彩的图形是由点、线、面、体组成。点是构成图形的基本元素。
2、点无大小,线有直线和曲线,面有平的面和曲的面。
3、点动成线,线动成面,面动成体。
4、体由面围成,面与面相交成线,线与线相交成点。
5、……
●你学到了什么?
B
1.电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于( )
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
2.在一个棱柱中,一共有八个面,则这个棱柱棱的条数有( )
A.18条
B.15条
C.12条
D.21条
A
3.下列立体图形中,面数相同的是( )
①正方体;②圆柱;③四棱柱;④圆锥.
A.①②
B.①③
C.②③
D.③④
D
B
4.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A.
B.
C.
D.
解:(1)18﹣2=16,答:这是十六棱柱.
(2)侧棱长为64÷16=4(cm),
S侧=4×3×16=192(cm2).
答:侧面积是192cm2.
5.一个棱柱有18个面,且所有的侧棱长的和为64cm,底面边长都是3cm.
(1)这是几棱柱?
(2)求此棱柱的侧面积.
第四章
几何图形
4.1
几何图形
4.1.2
点、线、面、体
图片引入
下图是一些立体图形的展开图,用它们能围成怎样的立体图形?
立方体
圆柱
三棱柱
圆锥
以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
拓展1:你有办法将图形(1)、(3)修改后使能折叠成棱柱?
拓展2:图形(2)、(4)是不同的平面图形,折叠出同样的棱柱,从中你得到了什么启示?
想一想、折一折
5
6
4
3
2
F
E
A
B
C
1
祝
你
前
程
似
锦
D
下面图形中,哪些是正方体的平面展开图?
考考你
是
是
不是
1.能结合几何模型或身边环境,指出体、面、线、点,并能区分平面和曲面、直线和曲线.
2.能从运动、集合的角度描述点、线、面、体的关系,并能恰当地举例来说明它们的关系.
3.初步体会“具体→抽象→具体”的认知方法.
知识点1:体和面
【问题探究】
你能找出常见的几何体吗?
归纳:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体简称体
常见的立体图形
包围着体的是面。面有平的面和曲的面两种
长方体
正方体
圆柱
圆锥
球
棱柱
棱锥
面
平面
曲面
练习:围成下面这些立体图形的各个面中,哪些面是平的?哪些面是曲的?
平面
曲面
知识点2:线和点
【问题探究】
想一想,举出生活中符合线、点形象的例子.
线的形象
线:直线和曲线
点的形象
点
点是构成图形的基本元素
面与面相交的地方形成线
体会:
知识点3:点、线、面、体的关系
【问题探究1】
物体的运动会留下运动轨迹,这些运动轨迹往往也能抽象成几何图形.如果把笔尖看成一个点,这个点在纸上运动时,形成的图形是什么?动手试一试.
归纳结论:
点动成线.
点动成线.
?
例
点动成线
线动成面.
【问题探究2】
汽车的雨刷在挡风玻璃上画出一个扇面,从几何的角度观察这种现象,你可以得出什么结论?
线动成面.
概括结论:
例
线动成面
面动成体.
【问题探究3】
既然“点动成线,线动成面”,那么请同学们想一想:当面运动时又会形成什么图形?如何验证你的猜想?
概括结论:
面动成体.
例
三角形绕一边旋转成圆锥体
长方形绕一边旋转成圆柱体
如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,把有对应关系的平面图形与立体图形连接起来.
【跟踪训练】
连一连
归纳总结
归纳总结
点动成——
线动成——
面动成——
线
面
体
体是由面组成
面与面相交成线
线与线相交成点
判定几何体点、线、面的个数
【举一反三】
下图是一个长方体的模型,它有几个面?面和面相交的地方形成了几条线?线和线相交成几个点?
6个面
12条线
8个点
·
·
·
·
·
·
·
·
【思考交流】
旋转形成几何体的体积
在长方形ABCD中,AB=2,BC=3,把该图形沿着一边所在直线旋转一周,求所围成的几何体的体积.
解:分两种情况:
①当绕AB旋转时,则V=πBC2×AB=18π;
②当绕BC旋转时,则V=πAB2×BC=12π.
答:所围成的几何体的体积为18π或12π.
分析:矩形绕一边旋转后得到圆柱,根据圆柱的体积公式,分两种情况讨论可得出答案.
点、线、面的规律探究
【迁移应用】
如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有_____个面,______条棱,______个顶点;
(2)六棱柱有_____个面,______条棱,______个顶点;
(3)由此猜想n棱柱有_____个面,______条棱,_______个顶点.
(4)你发现棱柱的面数、棱数与顶点数之间存在怎样的数量关系?
分析:结合三棱柱、四棱柱、五棱柱和六棱柱的特点,可知n棱柱面、棱和顶点的个数.
解:四棱柱有6个面,12条棱,8个顶点;
六棱柱有8个面,18条棱,12个顶点;
由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
答:因为(n+2)+2n-3n=2,
所以发现棱柱的面数﹢顶点数﹣棱数﹦2.
1、多姿多彩的图形是由点、线、面、体组成。点是构成图形的基本元素。
2、点无大小,线有直线和曲线,面有平的面和曲的面。
3、点动成线,线动成面,面动成体。
4、体由面围成,面与面相交成线,线与线相交成点。
5、……
●你学到了什么?
B
1.电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于( )
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
2.在一个棱柱中,一共有八个面,则这个棱柱棱的条数有( )
A.18条
B.15条
C.12条
D.21条
A
3.下列立体图形中,面数相同的是( )
①正方体;②圆柱;③四棱柱;④圆锥.
A.①②
B.①③
C.②③
D.③④
D
B
4.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A.
B.
C.
D.
解:(1)18﹣2=16,答:这是十六棱柱.
(2)侧棱长为64÷16=4(cm),
S侧=4×3×16=192(cm2).
答:侧面积是192cm2.
5.一个棱柱有18个面,且所有的侧棱长的和为64cm,底面边长都是3cm.
(1)这是几棱柱?
(2)求此棱柱的侧面积.
