2021-2022学年人教版数学七年级上册4.3.2 角的比较与运算 课件(共29张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册4.3.2 角的比较与运算 课件(共29张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览



文档简介
(共29张PPT)
第四章
几何图形初步
4.3
角
4.3.2
角的比较与运算
B
A
C
E
D
F
图片导入
A
B
C
D
AB>CD
A
B
C
D
AB=CD
A
A
B
C
D
AB<CD
类比线段大小的比较,你认为该如何比较两个角的大小?
1.运用类比的方法,学会比较两个角的大小,会分析图中角的和差关系.
2.通过动手操作,学会借助三角板拼出不同度数的角,认识角的平分线.
3.会进行简单的角的运算.
知识点1:角的大小比较
【问题探究】
如何比较下列两个角的大小?
A
O
B
A′
O′
B′
请每个学习小组的同学每人任意画出两个角,比较这两个角的大小,并讨论你们的比较方法.
类比探究
C
D
E
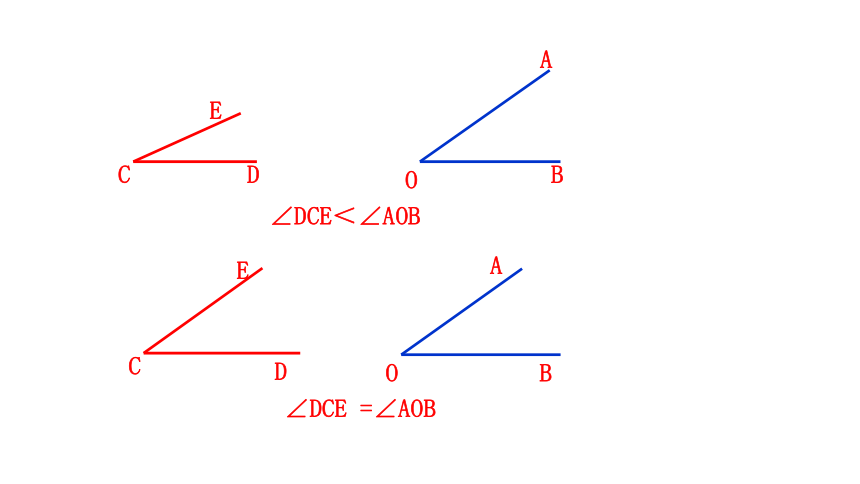
1.将两个角的顶点及一边重合
2.两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
叠合法
A
B
O
∠DCE>∠AOB
O
A
B
D
C
E
A
O
B
C
D
E
∠DCE<∠AOB
∠DCE
=∠AOB
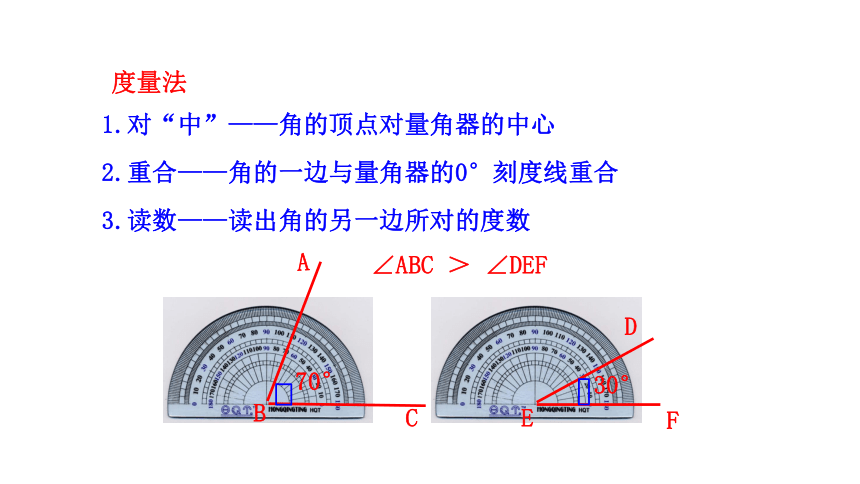
度量法
1.对“中”——角的顶点对量角器的中心
3.读数——读出角的另一边所对的度数
2.重合——角的一边与量角器的0°刻度线重合
B
C
A
F
E
D
70°
∠ABC
>
∠DEF
30°
常用的比较两个角的大小的方法有两种:
叠合法
度量法
归纳总结
两个角的大小关系有三种,记作:
(1)
∠ABC>∠DEF
(2)∠ABC<∠DEF
A
D
(E)
(F)
C
B
D
(E)
(F)
A
B
C
A
B
C
(3)∠ABC
=
∠DEF
(E)
(D)
(F)
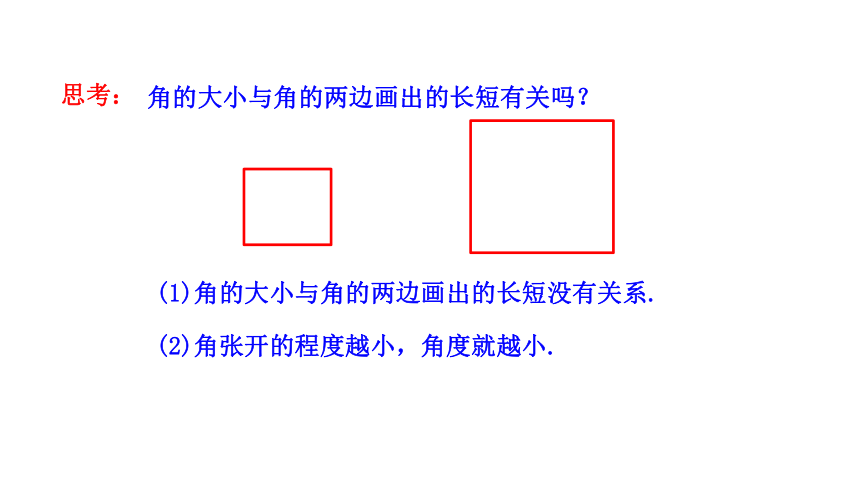
思考:
角的大小与角的两边画出的长短有关吗?
(1)角的大小与角的两边画出的长短没有关系.
(2)角张开的程度越小,角度就越小.
你知道放大镜不能“放大”角的度数的原因吗?
(1)图中共有几个角?分别是什么?
(2)这些角的角度有什么大小和等量关系?
解:共有3个角,分别是∠AOC、
∠AOB
、
∠BOC.
解:∠BOC
<
∠AOB
<
∠AOC
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
∠BOC=∠AOC-∠AOB.
类比探究
角的和差
填空:
(1)∠AOB=∠AOC+∠
(2)∠
=∠COD-∠AOC
(3)∠AOE=∠COE-∠
=∠AOD-∠
=∠COD-∠
-∠
BOC
AOC
DOE
AOD
AOC
DOE
C
B
A
D
E
o
练一练:
知识点2:角的平分线
类比探究
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
AOB
BOC
AOC
A
O
C
B
α
α
角的三等分线
O
A
B
D
C
射线OD,OC是∠AOB的三等分线
如何画一个角的平分线?你能想到什么方法?
1.度量法
2.对折法
动手操作
……
【跟踪训练】
填空:
(1)如图,∠AOB
=∠BOC
=∠COD,
OB
是_______的平分线,
________=
∠AOC,
________=
∠BOD,
∠BOC
=
_________
=
_______
=
________
∠AOC
∠BOC
∠BOC
∠AOC
∠BOD
∠AOD
B
C
D
O
A
A
B
C
D
E
(2)
因为AD是∠BAC的平分线,
所以∠_____=
∠______
因为∠ABC
=
2∠ABE,
所以_______平分∠______
(
角平分线的定义
).
BAD
CAD
BE
ABC
(
角平分线的定义
).
合作探究
都是15°的正整数倍
每个角都可以用其他角的和或差表示。
利用三角尺可以画出哪些度数的角?
75°
15°
从这些角度中,你能发现什么样的规律?
15°、30°、45°、60°、75°、90°、
105°、120°、135°、150°、165°、180°.
【跟踪训练】
1
2
1
2
1.
估计图中∠1与∠2的大小关系,并用适当的方法检验.
例
1
如图,O是直线上一点,∠AOC=53°17′,
求∠BOC的度数。
解:由题意可知,∠AOB是平角,∠AOB=∠AOC+∠BOC.
所以∠BOC=∠AOB-∠AOC=180°-53°17′=126°43′.
【例题讲解】
想一想
分析:AB是直线,∠AOB是平角,∠BOC与∠AOC的和是∠AOB.
【跟踪训练】
填空:如图(1)若∠AOC=32
°,
∠BOC=43°,则∠AOB=________.
(2)若已知
∠AOB
=
68
°,
∠BOC=40°,则∠AOC=________.
你真棒
想一想,议一议
C
B
O
A
32°
43°
75
°
28
°
角的比较与运算推理
【举一反三】
图中∠1=
∠2,
试判断∠BAD和∠EAC的大小,
并说明理由.
解:∠BAD=∠EAC.
理由:因为∠1=∠2,
又因为∠BAD=∠2+∠DAC,
∠EAC=∠1+∠DAC,
所以∠BAD=∠EAC.
【思考交流】
角的平分线及其应用
如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠EOB的度数.
分析:设∠DOE=2x,根据题意得到∠BOE=3x,∠AOC=∠COD=80°-2x,再根据平角为180°,得到2(80°-2x)+5x=180°,解得x=20°,即可得到∠BOE的度数.
解:设∠DOE=2x,因为∠DOE:∠BOD=2:5,所以∠BOE=3x.
又因为OC是∠AOD的平分线,∠COE=80°,
所以∠AOC=∠COD=80°-2x,所以2(80°-2x)+5x=180°.
解得x=20°,所以∠BOE=3x=3×20°=60°.
注意:应用角平分线解题时常用到数形结合的思想,借助图形寻找角之间的和、差、倍、分关系是解题的关键,往往需要借助方程列出等量关系求解.
角的和差运算中的分类讨论思想
【迁移应用】
已知∠AOB=40°,∠BOC=20°,求∠AOC的度数.
分析:本题需分情况讨论,一种情况是射线OC在∠AOB的内部,一种情况是射线OC在∠AOB的外部.
解:当射线OC在∠AOB的内部时,如图1,∠AOC=∠AOB-∠BOC=20°;
当射线OC在∠AOB的外部时,如图2,∠AOC=∠AOB+∠BOC=60°.
1.角的大小比较
2.角平分线定义
3.角的运算
1.若∠1=50°5′,∠2=50.5°,则∠1与∠2的大小关系是( )
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法确定
C
2.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,
则∠AOD的度数为( )
A.150°
B.145°
C.140°
D.135°
D
A
3.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
A.65°
B.50°
C.40°
D.25°
B
解:根据翻折可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
因为∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
所以∠ABE+∠DBC=90°,又∠CBD=66°,所以∠ABE=24°.
4.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠CBD=66°,则∠ABE为( )
A.20°
B.24°
C.40°
D.50°
5.如图,已知直线AB,CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠BOD的度数是_______.
解:因为OC平分∠DOB,
所以∠DOC=∠BOC=22°36′.
因为∠AOC=∠AOB+∠BOC=90°,
所以∠AOB=∠AOC﹣∠BOC=90°﹣22°36′=67°24′.
A
D
B
E
C
O
70°
6.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=22°36′,求∠BOA度数.
第四章
几何图形初步
4.3
角
4.3.2
角的比较与运算
B
A
C
E
D
F
图片导入
A
B
C
D
AB>CD
A
B
C
D
AB=CD
A
A
B
C
D
AB<CD
类比线段大小的比较,你认为该如何比较两个角的大小?
1.运用类比的方法,学会比较两个角的大小,会分析图中角的和差关系.
2.通过动手操作,学会借助三角板拼出不同度数的角,认识角的平分线.
3.会进行简单的角的运算.
知识点1:角的大小比较
【问题探究】
如何比较下列两个角的大小?
A
O
B
A′
O′
B′
请每个学习小组的同学每人任意画出两个角,比较这两个角的大小,并讨论你们的比较方法.
类比探究
C
D
E
1.将两个角的顶点及一边重合
2.两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
叠合法
A
B
O
∠DCE>∠AOB
O
A
B
D
C
E
A
O
B
C
D
E
∠DCE<∠AOB
∠DCE
=∠AOB
度量法
1.对“中”——角的顶点对量角器的中心
3.读数——读出角的另一边所对的度数
2.重合——角的一边与量角器的0°刻度线重合
B
C
A
F
E
D
70°
∠ABC
>
∠DEF
30°
常用的比较两个角的大小的方法有两种:
叠合法
度量法
归纳总结
两个角的大小关系有三种,记作:
(1)
∠ABC>∠DEF
(2)∠ABC<∠DEF
A
D
(E)
(F)
C
B
D
(E)
(F)
A
B
C
A
B
C
(3)∠ABC
=
∠DEF
(E)
(D)
(F)
思考:
角的大小与角的两边画出的长短有关吗?
(1)角的大小与角的两边画出的长短没有关系.
(2)角张开的程度越小,角度就越小.
你知道放大镜不能“放大”角的度数的原因吗?
(1)图中共有几个角?分别是什么?
(2)这些角的角度有什么大小和等量关系?
解:共有3个角,分别是∠AOC、
∠AOB
、
∠BOC.
解:∠BOC
<
∠AOB
<
∠AOC
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
∠BOC=∠AOC-∠AOB.
类比探究
角的和差
填空:
(1)∠AOB=∠AOC+∠
(2)∠
=∠COD-∠AOC
(3)∠AOE=∠COE-∠
=∠AOD-∠
=∠COD-∠
-∠
BOC
AOC
DOE
AOD
AOC
DOE
C
B
A
D
E
o
练一练:
知识点2:角的平分线
类比探究
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
AOB
BOC
AOC
A
O
C
B
α
α
角的三等分线
O
A
B
D
C
射线OD,OC是∠AOB的三等分线
如何画一个角的平分线?你能想到什么方法?
1.度量法
2.对折法
动手操作
……
【跟踪训练】
填空:
(1)如图,∠AOB
=∠BOC
=∠COD,
OB
是_______的平分线,
________=
∠AOC,
________=
∠BOD,
∠BOC
=
_________
=
_______
=
________
∠AOC
∠BOC
∠BOC
∠AOC
∠BOD
∠AOD
B
C
D
O
A
A
B
C
D
E
(2)
因为AD是∠BAC的平分线,
所以∠_____=
∠______
因为∠ABC
=
2∠ABE,
所以_______平分∠______
(
角平分线的定义
).
BAD
CAD
BE
ABC
(
角平分线的定义
).
合作探究
都是15°的正整数倍
每个角都可以用其他角的和或差表示。
利用三角尺可以画出哪些度数的角?
75°
15°
从这些角度中,你能发现什么样的规律?
15°、30°、45°、60°、75°、90°、
105°、120°、135°、150°、165°、180°.
【跟踪训练】
1
2
1
2
1.
估计图中∠1与∠2的大小关系,并用适当的方法检验.
例
1
如图,O是直线上一点,∠AOC=53°17′,
求∠BOC的度数。
解:由题意可知,∠AOB是平角,∠AOB=∠AOC+∠BOC.
所以∠BOC=∠AOB-∠AOC=180°-53°17′=126°43′.
【例题讲解】
想一想
分析:AB是直线,∠AOB是平角,∠BOC与∠AOC的和是∠AOB.
【跟踪训练】
填空:如图(1)若∠AOC=32
°,
∠BOC=43°,则∠AOB=________.
(2)若已知
∠AOB
=
68
°,
∠BOC=40°,则∠AOC=________.
你真棒
想一想,议一议
C
B
O
A
32°
43°
75
°
28
°
角的比较与运算推理
【举一反三】
图中∠1=
∠2,
试判断∠BAD和∠EAC的大小,
并说明理由.
解:∠BAD=∠EAC.
理由:因为∠1=∠2,
又因为∠BAD=∠2+∠DAC,
∠EAC=∠1+∠DAC,
所以∠BAD=∠EAC.
【思考交流】
角的平分线及其应用
如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠EOB的度数.
分析:设∠DOE=2x,根据题意得到∠BOE=3x,∠AOC=∠COD=80°-2x,再根据平角为180°,得到2(80°-2x)+5x=180°,解得x=20°,即可得到∠BOE的度数.
解:设∠DOE=2x,因为∠DOE:∠BOD=2:5,所以∠BOE=3x.
又因为OC是∠AOD的平分线,∠COE=80°,
所以∠AOC=∠COD=80°-2x,所以2(80°-2x)+5x=180°.
解得x=20°,所以∠BOE=3x=3×20°=60°.
注意:应用角平分线解题时常用到数形结合的思想,借助图形寻找角之间的和、差、倍、分关系是解题的关键,往往需要借助方程列出等量关系求解.
角的和差运算中的分类讨论思想
【迁移应用】
已知∠AOB=40°,∠BOC=20°,求∠AOC的度数.
分析:本题需分情况讨论,一种情况是射线OC在∠AOB的内部,一种情况是射线OC在∠AOB的外部.
解:当射线OC在∠AOB的内部时,如图1,∠AOC=∠AOB-∠BOC=20°;
当射线OC在∠AOB的外部时,如图2,∠AOC=∠AOB+∠BOC=60°.
1.角的大小比较
2.角平分线定义
3.角的运算
1.若∠1=50°5′,∠2=50.5°,则∠1与∠2的大小关系是( )
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法确定
C
2.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,
则∠AOD的度数为( )
A.150°
B.145°
C.140°
D.135°
D
A
3.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
A.65°
B.50°
C.40°
D.25°
B
解:根据翻折可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
因为∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
所以∠ABE+∠DBC=90°,又∠CBD=66°,所以∠ABE=24°.
4.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠CBD=66°,则∠ABE为( )
A.20°
B.24°
C.40°
D.50°
5.如图,已知直线AB,CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠BOD的度数是_______.
解:因为OC平分∠DOB,
所以∠DOC=∠BOC=22°36′.
因为∠AOC=∠AOB+∠BOC=90°,
所以∠AOB=∠AOC﹣∠BOC=90°﹣22°36′=67°24′.
A
D
B
E
C
O
70°
6.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=22°36′,求∠BOA度数.
