2021-2022学年人教版 八年级数学上册12.3 角平分线的性质 同步课时训练(word解析版)
文档属性
| 名称 | 2021-2022学年人教版 八年级数学上册12.3 角平分线的性质 同步课时训练(word解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 437.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览



文档简介
人教版
八年级数学上册
12.3
角平分线的性质
同步课时训练
一、选择题
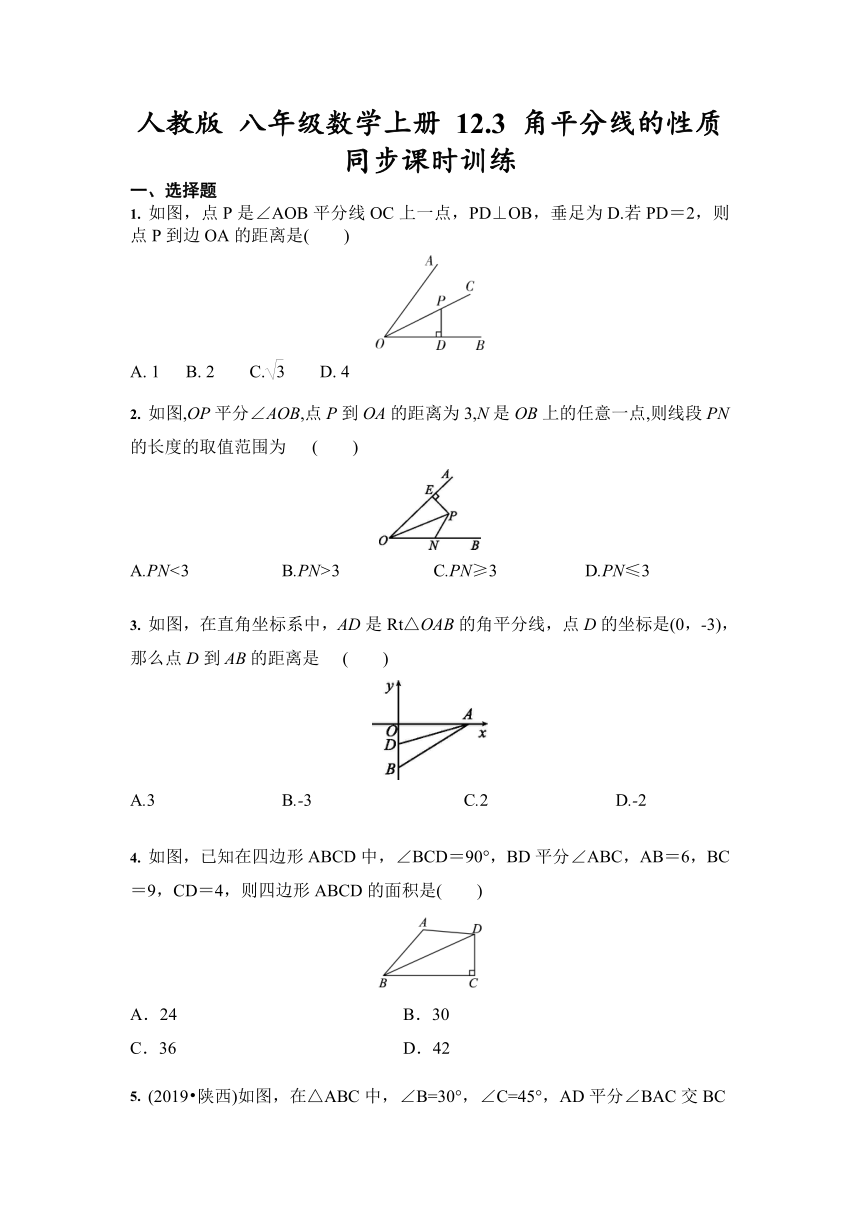
1.
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D.若PD=2,则点P到边OA的距离是( )
A.
1
B.
2
C.
D.
4
2.
如图,OP平分∠AOB,点P到OA的距离为3,N是OB上的任意一点,则线段PN的长度的取值范围为
( )
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
3.
如图,在直角坐标系中,AD是Rt△OAB的角平分线,点D的坐标是(0,-3),那么点D到AB的距离是
( )
A.3
B.-3
C.2
D.-2
4.
如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24
B.30
C.36
D.42
5.
(2019?陕西)如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为
A.2+
B.
C.
D.3
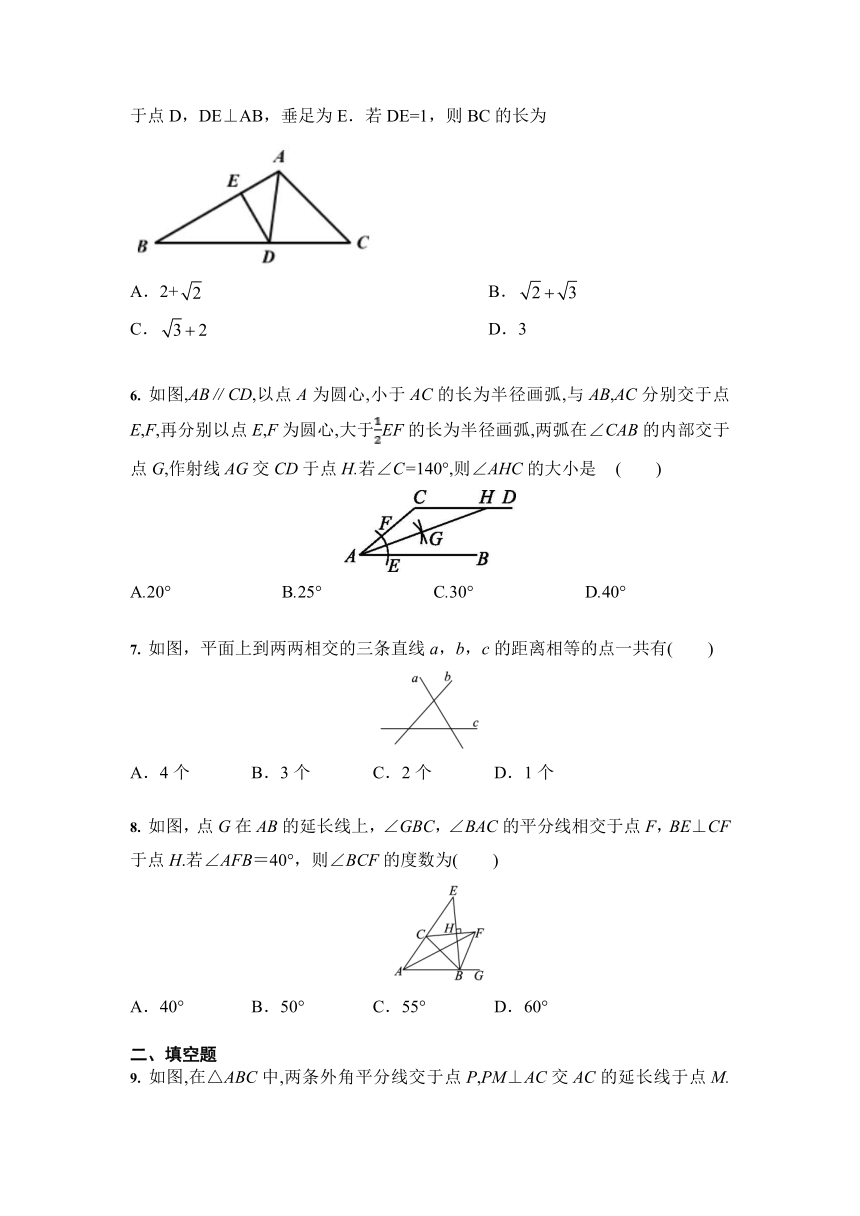
6.
如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,与AB,AC分别交于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠CAB的内部交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是
( )
A.20°
B.25°
C.30°
D.40°
7.
如图,平面上到两两相交的三条直线a,b,c的距离相等的点一共有( )
A.4个
B.3个
C.2个
D.1个
8.
如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF于点H.若∠AFB=40°,则∠BCF的度数为( )
A.40°
B.50°
C.55°
D.60°
二、填空题
9.
如图,在△ABC中,两条外角平分线交于点P,PM⊥AC交AC的延长线于点M.若PM=6
cm,则点P到AB的距离为 .?
10.
△ABC的周长为8,面积为10,若其内部一点O到三边的距离相等,则点O到AB的距离为________.
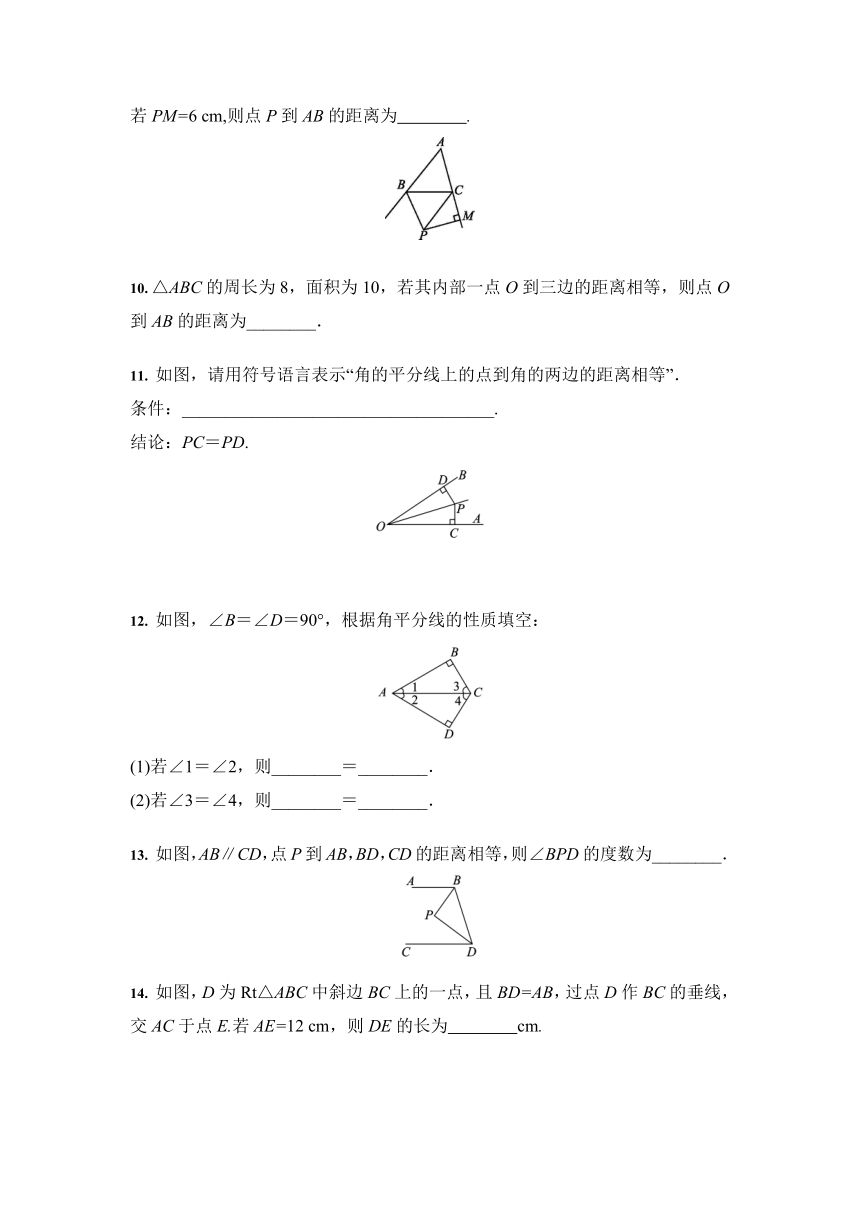
11.
如图,请用符号语言表示“角的平分线上的点到角的两边的距离相等”.
条件:____________________________________.
结论:PC=PD.
12.
如图,∠B=∠D=90°,根据角平分线的性质填空:
(1)若∠1=∠2,则________=________.
(2)若∠3=∠4,则________=________.
13.
如图,AB∥CD,点P到AB,BD,CD的距离相等,则∠BPD的度数为________.
14.
如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过点D作BC的垂线,交AC于点E.若AE=12
cm,则DE的长为 cm.?
15.
如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC= .?
16.
如图,P是△ABC外的一点,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,连接PB,PC.若PD=PE=PF,∠BAC=64°,则∠BPC的度数为________.
三、解答题
17.
如图,在∠AOB的两边OA,OB上分别取点D,M和点E,N,使OM=ON,OD=OE,DN和EM相交于点C.
求证:点C在∠AOB的平分线上.
18.
如图,在△ABC中,∠B=90°,两直角边AB=7,BC=24,斜边AC=25,P是角平分线AP,CP的交点,PE⊥AB,PF⊥BC,PD⊥AC,垂足分别为E,F,D,求PD的长.
19.
如图,点B,C分别在∠A的两边上,D是∠A内一点,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=AC,DE=DF.求证:BD=CD.
20.
如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M,N.求证:PM=PN.
人教版
八年级数学上册
12.3
角平分线的性质
同步课时训练-答案
一、选择题
1.
【答案】B 【解析】如解图,过点P作PG⊥OA于点G,根据角平分线上的点到角的两边距离相等可得,PG=PD=2.
2.
【答案】C [解析]
作PM⊥OB于点M.∵OP平分∠AOB,PE⊥OA,PM⊥OB,∴PM=PE=3.∴PN≥3.
3.
【答案】A [解析]
如图,过点D作DE⊥AB于点E.
∵点D的坐标是(0,-3),
∴OD=3.
∵AD是△OAB的角平分线,
∴ED=OD=3,
即点D到AB的距离是3.
4.
【答案】B [解析]
过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4.
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
5.
【答案】A
【解析】如图,过点D作DF⊥AC于F,
∵AD为∠BAC的平分线,且DE⊥AB于E,DF⊥AC于F,∴DF=DE=1,
在Rt△BED中,∠B=30°,∴BD=2DE=2,
在Rt△CDF中,∠C=45°,∴△CDF为等腰直角三角形,
∴CF=DF=1,∴CD==,
∴BC=BD+CD=,故选A.
6.
【答案】A [解析]
由题意可得AH平分∠CAB.
∵AB∥CD,
∴∠C+∠CAB=180°,∠HAB=∠AHC.
∵∠ACD=140°,∴∠CAB=40°.
∵AH平分∠CAB,∴∠HAB=20°.
∴∠AHC=20°.
7.
【答案】A [解析]
如图,到三条直线a,b,c的距离相等的点一共有4个.
8.
【答案】B [解析]
如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.
∵AF平分∠BAC,FZ⊥AE,FW⊥AB,
∴FZ=FW.同理FW=FY.
∴FZ=FY.
又∵FZ⊥AE,FY⊥CB,
∴∠FCZ=∠FCY.
由∠AFB=40°,易得∠ACB=80°.
∴∠ZCY=100°.∴∠BCF=50°.
二、填空题
9.
【答案】6
cm [解析]
如图,过点P作PN⊥BC于点N,PQ⊥AB交AB的延长线于点Q.∵BP,CP是两条外角的平分线,PM⊥AC,∴PN=PM,PQ=PN.∴PQ=PM.
∵PM=6
cm,∴PQ=6
cm,即点P到AB的距离为6
cm.
10.
【答案】2.5 [解析]
设点O到AB,BC,AC的距离均为h,∴S△ABC=×8·h=10,解得h=2.5,即点O到AB的距离为2.5.
11.
【答案】∠AOP=∠BOP,PC⊥OA于点C,PD⊥OB于点D
12.
【答案】(1)BC CD (2)AB AD
13.
【答案】90° [解析]
∵点P到AB,BD,CD的距离相等,∴BP,DP分别平分∠ABD,∠BDC.
∵AB∥CD,∴∠ABD+∠BDC=180°.
∴∠PBD+∠PDB=90°.故∠BPD=90°.
14.
【答案】12 [解析]
如图,连接BE.∵D为Rt△ABC中斜边BC上的一点,过点D作BC的垂线,交AC于点E,∴∠A=∠BDE=90°.
在Rt△DBE和Rt△ABE中,
∴Rt△DBE≌Rt△ABE(HL).∴DE=AE.∵AE=12
cm,∴DE=12
cm.
15.
【答案】7 [解析]
过点P作PF⊥BC于点F,PG⊥AB于点G,连接AP.∵△ABC的两条外角平分线BP,CP相交于点P,∴PF=PG=PE=2.∵S△BPC=2,∴BC·2=2,解得BC=2.∵△ABC的周长为11,
∴AC+AB=11-2=9.
∴S△ABC=S△ACP+S△ABP-S△BPC=AC·PE+AB·PG-S△BPC=×9×2-2=7.
16.
【答案】32° [解析]
∵PD=PE=PF,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,
∴CP平分∠ACF,BP平分∠ABC.
∴∠PCF=∠ACF,∠PBF=∠ABC.
∴∠BPC=∠PCF-∠PBF=(∠ACF-∠ABC)=∠BAC=32°.
三、解答题
17.
【答案】
证明:如图,过点C作CG⊥OA于点G,CF⊥OB于点F.
在△MOE和△NOD中,
∴△MOE≌△NOD(SAS).
∴S△MOE=S△NOD.
∴S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,
即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.
∵OM=ON,OD=OE,
∴DM=EN.∴CG=CF.
又∵CG⊥OA,CF⊥OB,
∴点C在∠AOB的平分线上.
18.
【答案】
解:连接BP.
∵P是角平分线AP,CP的交点,PE⊥AB,PF⊥BC,PD⊥AC,
∴PE=PD=PF.
设PE=PD=PF=x.
∵S△ABC=AB·BC=84,
S△ABC=AB·x+AC·x+BC·x=(AB+AC+BC)·x=×56x=28x,
∴28x=84,解得x=3.故PD的长为3.
19.
【答案】
证明:如图,连接AD.
∵DE⊥AB,DF⊥AC,DE=DF,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).∴BD=CD.
20.
【答案】
证明:∵BD是∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS).
∴∠ADB=∠CDB.
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
八年级数学上册
12.3
角平分线的性质
同步课时训练
一、选择题
1.
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D.若PD=2,则点P到边OA的距离是( )
A.
1
B.
2
C.
D.
4
2.
如图,OP平分∠AOB,点P到OA的距离为3,N是OB上的任意一点,则线段PN的长度的取值范围为
( )
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
3.
如图,在直角坐标系中,AD是Rt△OAB的角平分线,点D的坐标是(0,-3),那么点D到AB的距离是
( )
A.3
B.-3
C.2
D.-2
4.
如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24
B.30
C.36
D.42
5.
(2019?陕西)如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为
A.2+
B.
C.
D.3
6.
如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,与AB,AC分别交于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠CAB的内部交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是
( )
A.20°
B.25°
C.30°
D.40°
7.
如图,平面上到两两相交的三条直线a,b,c的距离相等的点一共有( )
A.4个
B.3个
C.2个
D.1个
8.
如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF于点H.若∠AFB=40°,则∠BCF的度数为( )
A.40°
B.50°
C.55°
D.60°
二、填空题
9.
如图,在△ABC中,两条外角平分线交于点P,PM⊥AC交AC的延长线于点M.若PM=6
cm,则点P到AB的距离为 .?
10.
△ABC的周长为8,面积为10,若其内部一点O到三边的距离相等,则点O到AB的距离为________.
11.
如图,请用符号语言表示“角的平分线上的点到角的两边的距离相等”.
条件:____________________________________.
结论:PC=PD.
12.
如图,∠B=∠D=90°,根据角平分线的性质填空:
(1)若∠1=∠2,则________=________.
(2)若∠3=∠4,则________=________.
13.
如图,AB∥CD,点P到AB,BD,CD的距离相等,则∠BPD的度数为________.
14.
如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过点D作BC的垂线,交AC于点E.若AE=12
cm,则DE的长为 cm.?
15.
如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC= .?
16.
如图,P是△ABC外的一点,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,连接PB,PC.若PD=PE=PF,∠BAC=64°,则∠BPC的度数为________.
三、解答题
17.
如图,在∠AOB的两边OA,OB上分别取点D,M和点E,N,使OM=ON,OD=OE,DN和EM相交于点C.
求证:点C在∠AOB的平分线上.
18.
如图,在△ABC中,∠B=90°,两直角边AB=7,BC=24,斜边AC=25,P是角平分线AP,CP的交点,PE⊥AB,PF⊥BC,PD⊥AC,垂足分别为E,F,D,求PD的长.
19.
如图,点B,C分别在∠A的两边上,D是∠A内一点,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=AC,DE=DF.求证:BD=CD.
20.
如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M,N.求证:PM=PN.
人教版
八年级数学上册
12.3
角平分线的性质
同步课时训练-答案
一、选择题
1.
【答案】B 【解析】如解图,过点P作PG⊥OA于点G,根据角平分线上的点到角的两边距离相等可得,PG=PD=2.
2.
【答案】C [解析]
作PM⊥OB于点M.∵OP平分∠AOB,PE⊥OA,PM⊥OB,∴PM=PE=3.∴PN≥3.
3.
【答案】A [解析]
如图,过点D作DE⊥AB于点E.
∵点D的坐标是(0,-3),
∴OD=3.
∵AD是△OAB的角平分线,
∴ED=OD=3,
即点D到AB的距离是3.
4.
【答案】B [解析]
过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4.
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
5.
【答案】A
【解析】如图,过点D作DF⊥AC于F,
∵AD为∠BAC的平分线,且DE⊥AB于E,DF⊥AC于F,∴DF=DE=1,
在Rt△BED中,∠B=30°,∴BD=2DE=2,
在Rt△CDF中,∠C=45°,∴△CDF为等腰直角三角形,
∴CF=DF=1,∴CD==,
∴BC=BD+CD=,故选A.
6.
【答案】A [解析]
由题意可得AH平分∠CAB.
∵AB∥CD,
∴∠C+∠CAB=180°,∠HAB=∠AHC.
∵∠ACD=140°,∴∠CAB=40°.
∵AH平分∠CAB,∴∠HAB=20°.
∴∠AHC=20°.
7.
【答案】A [解析]
如图,到三条直线a,b,c的距离相等的点一共有4个.
8.
【答案】B [解析]
如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.
∵AF平分∠BAC,FZ⊥AE,FW⊥AB,
∴FZ=FW.同理FW=FY.
∴FZ=FY.
又∵FZ⊥AE,FY⊥CB,
∴∠FCZ=∠FCY.
由∠AFB=40°,易得∠ACB=80°.
∴∠ZCY=100°.∴∠BCF=50°.
二、填空题
9.
【答案】6
cm [解析]
如图,过点P作PN⊥BC于点N,PQ⊥AB交AB的延长线于点Q.∵BP,CP是两条外角的平分线,PM⊥AC,∴PN=PM,PQ=PN.∴PQ=PM.
∵PM=6
cm,∴PQ=6
cm,即点P到AB的距离为6
cm.
10.
【答案】2.5 [解析]
设点O到AB,BC,AC的距离均为h,∴S△ABC=×8·h=10,解得h=2.5,即点O到AB的距离为2.5.
11.
【答案】∠AOP=∠BOP,PC⊥OA于点C,PD⊥OB于点D
12.
【答案】(1)BC CD (2)AB AD
13.
【答案】90° [解析]
∵点P到AB,BD,CD的距离相等,∴BP,DP分别平分∠ABD,∠BDC.
∵AB∥CD,∴∠ABD+∠BDC=180°.
∴∠PBD+∠PDB=90°.故∠BPD=90°.
14.
【答案】12 [解析]
如图,连接BE.∵D为Rt△ABC中斜边BC上的一点,过点D作BC的垂线,交AC于点E,∴∠A=∠BDE=90°.
在Rt△DBE和Rt△ABE中,
∴Rt△DBE≌Rt△ABE(HL).∴DE=AE.∵AE=12
cm,∴DE=12
cm.
15.
【答案】7 [解析]
过点P作PF⊥BC于点F,PG⊥AB于点G,连接AP.∵△ABC的两条外角平分线BP,CP相交于点P,∴PF=PG=PE=2.∵S△BPC=2,∴BC·2=2,解得BC=2.∵△ABC的周长为11,
∴AC+AB=11-2=9.
∴S△ABC=S△ACP+S△ABP-S△BPC=AC·PE+AB·PG-S△BPC=×9×2-2=7.
16.
【答案】32° [解析]
∵PD=PE=PF,PD⊥AB交BA的延长线于点D,PE⊥AC于点E,PF⊥BC交BC的延长线于点F,
∴CP平分∠ACF,BP平分∠ABC.
∴∠PCF=∠ACF,∠PBF=∠ABC.
∴∠BPC=∠PCF-∠PBF=(∠ACF-∠ABC)=∠BAC=32°.
三、解答题
17.
【答案】
证明:如图,过点C作CG⊥OA于点G,CF⊥OB于点F.
在△MOE和△NOD中,
∴△MOE≌△NOD(SAS).
∴S△MOE=S△NOD.
∴S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,
即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.
∵OM=ON,OD=OE,
∴DM=EN.∴CG=CF.
又∵CG⊥OA,CF⊥OB,
∴点C在∠AOB的平分线上.
18.
【答案】
解:连接BP.
∵P是角平分线AP,CP的交点,PE⊥AB,PF⊥BC,PD⊥AC,
∴PE=PD=PF.
设PE=PD=PF=x.
∵S△ABC=AB·BC=84,
S△ABC=AB·x+AC·x+BC·x=(AB+AC+BC)·x=×56x=28x,
∴28x=84,解得x=3.故PD的长为3.
19.
【答案】
证明:如图,连接AD.
∵DE⊥AB,DF⊥AC,DE=DF,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).∴BD=CD.
20.
【答案】
证明:∵BD是∠ABC的平分线,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
∴△ABD≌△CBD(SAS).
∴∠ADB=∠CDB.
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
