1.2空间向量基本定理课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共16张PPT)
文档属性
| 名称 | 1.2空间向量基本定理课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1.2
空间向量基本定理
(第一课时)
第一章
空间向量与立体几何
2.平面向量的正交分解
复习回顾
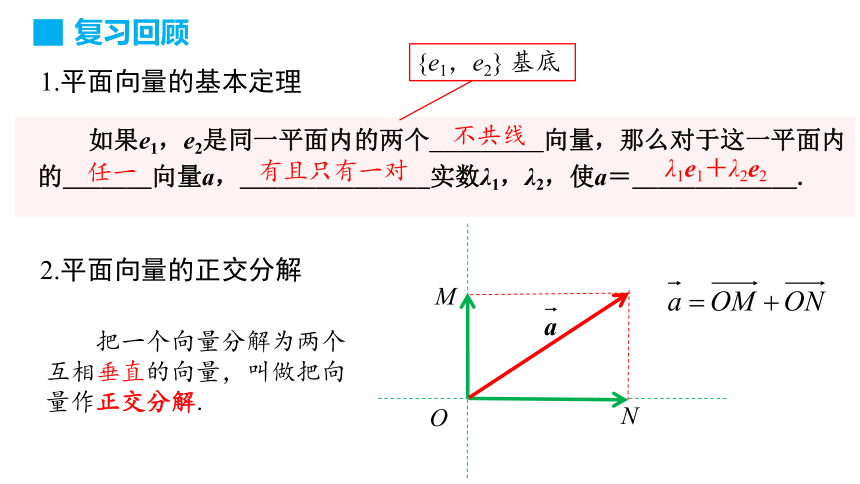
如果e1,e2是同一平面内的两个_________向量,那么对于这一平面内的_______向量a,_______________实数λ1,λ2,使a=_____________.
1.平面向量的基本定理
不共线
任一
有且只有一对
λ1e1+λ2e2
{e1,e2}
基底
M
N
O
把一个向量分解为两个互相垂直的向量,叫做把向量作正交分解.
猜想
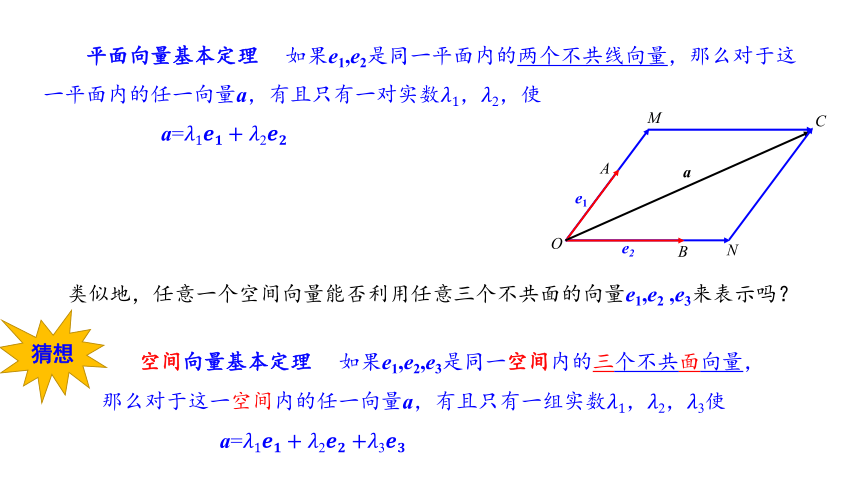
平面向量基本定理
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数2,使
a=2
类似地,任意一个空间向量能否利用任意三个不共面的向量e1,e2
,e3来表示吗?
a
e1
e2
O
A
M
C
B
N
空间向量基本定理
如果e1,e2,e3是同一空间内的三个不共面向量,那么对于这一空间内的任一向量a,有且只有一组实数23使
a=2
3
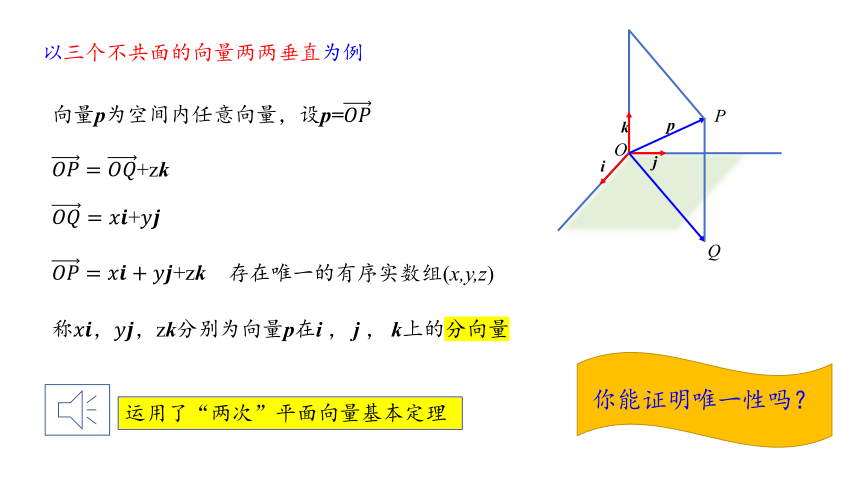
以三个不共面的向量两两垂直为例
i
k
j
p
P
Q
O
向量p为空间内任意向量,设p=
+zk
+
+zk
存在唯一的有序实数组(x,y,z)
zk分别为向量p在i
j
k上的分向量
你能证明唯一性吗?
运用了“两次”平面向量基本定理
+zk
+z1k
反证法
假设存在x1,y1,z1使得+z1k也成立
+z1k-zk
整理+z1-zk
不妨不相等
所以+k
,k
共面,与已知矛盾.
证明:
矛盾在哪里?
共面
探究1
在空间中,如果用任意三个不共面的向量a,
b,
c代替两两垂直的向量i,
j,
k,你能得出类似的结论吗?
定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得
p
=xa+yb+zc.
请你自己给出空间向量基本定理的证明.
a
c
b
p
P
P
′
O
A′
B′
C′
证明:
如图,设,b,c不共面,
过O点作,
A
C
B
过P作直线PP平行于直线OC,交平面OAB于点P
过P
作直线PA平行于直线OB,
作直线PB平行于直线OA,
作直线PC平行于直线OP
存在三个实数x,y,z满足,
+
阅读教材,回答下列问题
(1)什么是基底?什么是基向量?
(2)一个基底包含几个基向量?三个项链要构成一个基底需要满足什么条件?
(3)什么是单位正交基底?正交分解的定义是什么?
(4)为什么要对空间向量作正交分解?
注意
空间中任意三个不共面的向量都可以作为空间的一个基底;
因为向量0与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,隐含着它们都不为0;
一个基底是指一个向量组,而一个基向量是指基底中的某一个向量,二者是相关联的不同概念.
例题1
已知向量{a,b,c}是空间的一个基底.求证:向量a+b,a-b,c能构成空间的一个基底.
例题讲解
例题讲解
例2
如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且MN=
ON,AP=
,用向量
,
.
O
A
B
M
C
P
N
结合图形特征,利用三角形法则,平行四边形法则,数乘运算解决问题.
巩固练习
P12课后练习1,2,3
1.2
空间向量基本定理
(第二课时)
第一章
空间向量与立体几何
空间向量基本定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得
p
=xa+yb+zc.
{a,b,c}叫做一个基底
复习回顾
例题讲解
例3
如图,在平行六面体ABCD-A1B1C1D1中,AB=4,
AD=4,AA1=5,∠DAB=60°,
∠BAA1=60°,
∠DAA1=60°,M,N分别为D1C1的中点.
求证:
MN⊥AC1.
A1
A
B
C
D
D1
C1
B1
M
N
线线垂直
例4
如图,正方体ABCD-A'B'C'D'的棱长为,E,
F,G分别为C'的中点.
(1)求证:EF//AC;
(2)求CE与AG所成角的余弦值.
A
A
B
C
D
D
C
B
E
F
G
线线平行
异面直线夹角
巩固练习
P14课后练习1,2,3
1.2
空间向量基本定理
(第一课时)
第一章
空间向量与立体几何
2.平面向量的正交分解
复习回顾
如果e1,e2是同一平面内的两个_________向量,那么对于这一平面内的_______向量a,_______________实数λ1,λ2,使a=_____________.
1.平面向量的基本定理
不共线
任一
有且只有一对
λ1e1+λ2e2
{e1,e2}
基底
M
N
O
把一个向量分解为两个互相垂直的向量,叫做把向量作正交分解.
猜想
平面向量基本定理
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数2,使
a=2
类似地,任意一个空间向量能否利用任意三个不共面的向量e1,e2
,e3来表示吗?
a
e1
e2
O
A
M
C
B
N
空间向量基本定理
如果e1,e2,e3是同一空间内的三个不共面向量,那么对于这一空间内的任一向量a,有且只有一组实数23使
a=2
3
以三个不共面的向量两两垂直为例
i
k
j
p
P
Q
O
向量p为空间内任意向量,设p=
+zk
+
+zk
存在唯一的有序实数组(x,y,z)
zk分别为向量p在i
j
k上的分向量
你能证明唯一性吗?
运用了“两次”平面向量基本定理
+zk
+z1k
反证法
假设存在x1,y1,z1使得+z1k也成立
+z1k-zk
整理+z1-zk
不妨不相等
所以+k
,k
共面,与已知矛盾.
证明:
矛盾在哪里?
共面
探究1
在空间中,如果用任意三个不共面的向量a,
b,
c代替两两垂直的向量i,
j,
k,你能得出类似的结论吗?
定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得
p
=xa+yb+zc.
请你自己给出空间向量基本定理的证明.
a
c
b
p
P
P
′
O
A′
B′
C′
证明:
如图,设,b,c不共面,
过O点作,
A
C
B
过P作直线PP平行于直线OC,交平面OAB于点P
过P
作直线PA平行于直线OB,
作直线PB平行于直线OA,
作直线PC平行于直线OP
存在三个实数x,y,z满足,
+
阅读教材,回答下列问题
(1)什么是基底?什么是基向量?
(2)一个基底包含几个基向量?三个项链要构成一个基底需要满足什么条件?
(3)什么是单位正交基底?正交分解的定义是什么?
(4)为什么要对空间向量作正交分解?
注意
空间中任意三个不共面的向量都可以作为空间的一个基底;
因为向量0与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,隐含着它们都不为0;
一个基底是指一个向量组,而一个基向量是指基底中的某一个向量,二者是相关联的不同概念.
例题1
已知向量{a,b,c}是空间的一个基底.求证:向量a+b,a-b,c能构成空间的一个基底.
例题讲解
例题讲解
例2
如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且MN=
ON,AP=
,用向量
,
.
O
A
B
M
C
P
N
结合图形特征,利用三角形法则,平行四边形法则,数乘运算解决问题.
巩固练习
P12课后练习1,2,3
1.2
空间向量基本定理
(第二课时)
第一章
空间向量与立体几何
空间向量基本定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得
p
=xa+yb+zc.
{a,b,c}叫做一个基底
复习回顾
例题讲解
例3
如图,在平行六面体ABCD-A1B1C1D1中,AB=4,
AD=4,AA1=5,∠DAB=60°,
∠BAA1=60°,
∠DAA1=60°,M,N分别为D1C1的中点.
求证:
MN⊥AC1.
A1
A
B
C
D
D1
C1
B1
M
N
线线垂直
例4
如图,正方体ABCD-A'B'C'D'的棱长为,E,
F,G分别为C'的中点.
(1)求证:EF//AC;
(2)求CE与AG所成角的余弦值.
A
A
B
C
D
D
C
B
E
F
G
线线平行
异面直线夹角
巩固练习
P14课后练习1,2,3
