安徽省蚌埠市2022届高三上学期第一次教学质量检查文科数学试题(Word版含答案)
文档属性
| 名称 | 安徽省蚌埠市2022届高三上学期第一次教学质量检查文科数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 379.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 12:37:30 | ||
图片预览



文档简介
蚌埠市2022届高三年级第一次教学质量检査考试
数学(文史类)
本试卷满分150分,考试时间120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,则(
)
A.
B.
C.
D.
2.已知i为虚数单位,复数z满足zi=-2+i,则=(
)
A.1+2i
B.-1+2i
C.1-2i
D.-1-2i
3.若a>0且a≠1,则“MN>0”是“"的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.我国在2020年开展了第七次全国人口普査,并于2021年5月11日公布了结果.自新中国成立以来,我国共进行了七次全国人口普査,下图为我国历次全国人口普査人口性别构成及总人口性别比(以女性为100,男性对女性的比例)统计图,则下列说法错误的是
A.近三次全国人口普查总人口性别比呈递减趋势
B.我国历次全国人口普查总人口数呈逐次递增
C.第五次全国人口普查时,我国总人口数已经突破12亿
D.第七次人口普查时,我国总人口性别比最高
5.已知x,y满足约束条件,则的最大值为(
)
A.-21
B.3
C.6
D.9
6.为得到函数的图象,只需将函数的图象(
)
A.向右平移个单位
B.向右平移个单位
C.向左平移个单位
D.向左平移个单位
7.若a>0,b>0,,则2a+b的最小值为(
)
A.6
B.
C.
D.
8.勒洛三角形是一种特殊三角形,指分别以正三角形的三个顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形.勒洛三角形的特点是:在任何方向上都有相同的宽度,即能在距离等于其圆弧半径(等于正三角形的边长)的两条平行线间自由转动,并且始终保持与两直线都接触.机械加工业上利用这个性质,把钻头的横截面做成勒洛三角形的形状,就能在零件上钻出正方形的孔来.如在勒洛三角形ABC内随机选取一点,则该点位于正三角形ABC内的概率为(
)
A.
B.
C.
D.
9.若定义域为R的奇函数f(x)满足f(1-x)=f(1+x),且f(3)=2,则f(2021)=(
)
A.2
B.1
C.0
D.-2
10.正四面体P-ABC中,点M是BC的中点,则异面直线PM与AB所成角的余弦值为(
)
A.
B.
C.
D.
11.已知椭圆的右顶点为A,坐标原点为0,若椭圆上存在一点P使得△OAP是等腰直角三角形,则该椭圆的离心率为(
)
A.
B.
C.
D.
12.设若关于x的方程有6个实数解,则实数a的取值范围是(
)
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量a=(2,-1),b=(t,2),若a∥b,则t=
.
14.以双曲线C:的一个焦点为圆心,以5为半径的圆,截该双曲线的一条渐近线所得的弦长为
.
15.已知为锐角,
,则
.
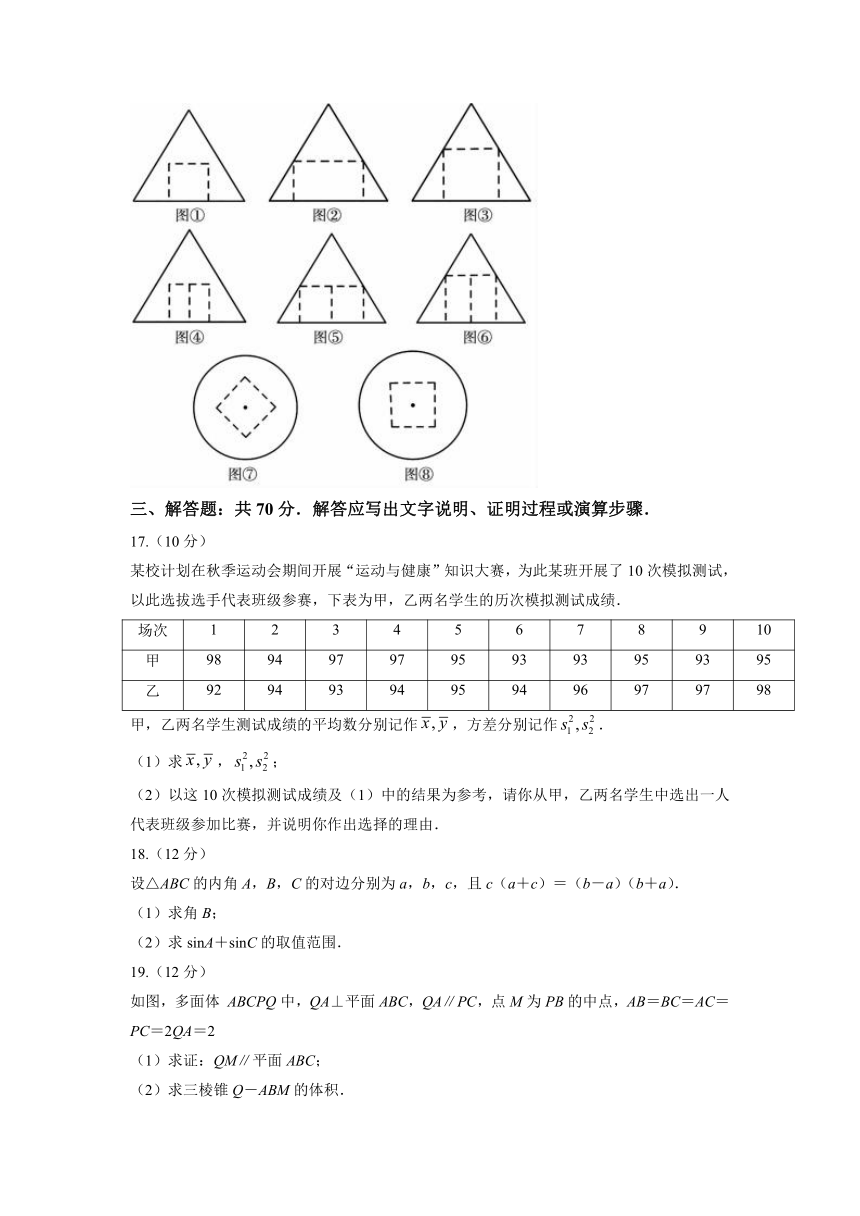
16.某零件的结构是在一个圆锥中挖去了一个正方体,且正方体的一个面与圆锥底面重合,该面所对的面的四个顶点在圆锥侧面内.在图①②③④⑤⑥⑦⑧中选两个分别作为该零件的主视图和俯视图,则所选主视图和俯视图的编号依次可能为
(写出符合要求的一组答案即可).
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
某校计划在秋季运动会期间开展“运动与健康”知识大赛,为此某班开展了10次模拟测试,以此选拔选手代表班级参赛,下表为甲,乙两名学生的历次模拟测试成绩.
场次
1
2
3
4
5
6
7
8
9
10
甲
98
94
97
97
95
93
93
95
93
95
乙
92
94
93
94
95
94
96
97
97
98
甲,乙两名学生测试成绩的平均数分别记作,方差分别记作.
(1)求,;
(2)以这10次模拟测试成绩及(1)中的结果为参考,请你从甲,乙两名学生中选出一人代表班级参加比赛,并说明你作出选择的理由.
18.(12分)
设△ABC的内角A,B,C的对边分别为a,b,c,且c(a+c)=(b-a)(b+a).
(1)求角B;
(2)求sinA+sinC的取值范围.
19.(12分)
如图,多面体
ABCPQ中,QA⊥平面ABC,QA∥PC,点M为PB的中点,AB=BC=AC=PC=2QA=2
(1)求证:QM∥平面ABC;
(2)求三棱锥Q-ABM的体积.
20.(12分)
已知数列的前n项和为,满足.
(1)求数列的通项公式;
(2)记,数列的前n项和为,求证:为定值.
21.(12分)
已知函数.
(1)求函数y=f(x)g(x)的极值;
(2)求证:.
22.(12分)
已知抛物线C:的焦点为F,点O为坐标原点,直线l过点T(4,0)与抛物线C相交于A,B两点(点A位于第一象限).
(1)求证:OA⊥OB;
(2)如图,连接AF,BF并延长分别交抛物线C于点,设直线AB的斜率为,直线,的斜率为,则是否为定值?若是,求出定值;若不是,说明理由.
蚌埠市2022届高三年级第一次教学质量检査考试
数学(文史类)参考答案及评分标准
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
D
C
D
B
A
D
B
C
A
二、填空题:
13.-4
14.8
15.
16.⑤⑦(或①⑧)
三、解答题:
17.(10分)
解:(1),
,………………2分
,
………………6分
(2)答案一:
由(1)可知,,甲,乙两人平均分相同,但甲发挥更稳定,所以可以派甲同学代表班级参赛.…………10分
答案二:
由(1)可知,
,甲,乙两人平均分相同,两人成绩的方差差距不大,但从10次测试成绩的增减趋势可以发现,甲的成绩总体呈下降趋势,乙的成绩总体呈上升趋势,说明乙的状态越来越好,所以可以派乙同学代表班级参赛.………………10分
18.(12分)
解:(1)由题意可得,,
,………………3分
由余弦定理得,即.………………6分
(2)由(1)可知,,
,……………………9分
又,所以,
即的取值范围是.………………12分
19.(12分)
解:(1)取BC中点H,连接MH,AH,由点M为PB的中点,
则MH∥PC且MH=PC,又QA∥PC且QA=PC,
所以,即四边形QAHM为平行四边形,………………3分
从而QM∥AH,而AH平面ABC,QM平面ABC,
所以QM∥平面ABC.……………………6分
(2)由(1)知,MH∥QA,QA平面QAB,MH平面QAB,
所以MH∥平面QAB,则点M到平面QAB的距离与点H到平面QAB的距离相等,即………………9分
由条件知,QA为三棱锥Q-ABH的高,
所以三棱锥Q-ABM的体积.………………12分
20.(12分)
解:(1)当n=1时,
,解得.
当n≥2时,,从而,
化简得,……………………3分
所以数列是首项为2,公比为2的等比数列,
则,即.………………5分
(2),
所以,
从而,
两式相减,得
,………………9分
即,所以,
而,
所以为定值.………………12分
21.(12分)
解:(1)记,定义域为,
则,………………2分
令,解得x=1,
列表如下:
x
(0,1)
1
-
-
0
+
F(x)
单调递减
单调递减
极小值
单调递增
结合表格可知函数y=f(x)g(x)极小值为F(1)=e,无极大值.………………5分
(2).
构造函数,定义域为,
………………8分
当x>0时,;当x<0时,
,
所以G(x)在上单调递减,在上单调递增,………………10分
当时,.
即.………………12分
22.(12分)
解:(1)设直线l方程为,
联立直线l与抛物线C的方程,
消去x,得,
故,又,………………3分
所以,
即.………………5分
(2)设,由焦点F(1,0),
设直线的方程为x=ny+1,
联立直线与抛物线C的方程,
消去x,得,
所以,则
,………………8分
同理可得,,
所以
,
又,所以,即为定值.……………………12分
(以上答案仅供参考,其它解法请参考以上评分标准酌情赋分)
数学(文史类)
本试卷满分150分,考试时间120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,则(
)
A.
B.
C.
D.
2.已知i为虚数单位,复数z满足zi=-2+i,则=(
)
A.1+2i
B.-1+2i
C.1-2i
D.-1-2i
3.若a>0且a≠1,则“MN>0”是“"的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.我国在2020年开展了第七次全国人口普査,并于2021年5月11日公布了结果.自新中国成立以来,我国共进行了七次全国人口普査,下图为我国历次全国人口普査人口性别构成及总人口性别比(以女性为100,男性对女性的比例)统计图,则下列说法错误的是
A.近三次全国人口普查总人口性别比呈递减趋势
B.我国历次全国人口普查总人口数呈逐次递增
C.第五次全国人口普查时,我国总人口数已经突破12亿
D.第七次人口普查时,我国总人口性别比最高
5.已知x,y满足约束条件,则的最大值为(
)
A.-21
B.3
C.6
D.9
6.为得到函数的图象,只需将函数的图象(
)
A.向右平移个单位
B.向右平移个单位
C.向左平移个单位
D.向左平移个单位
7.若a>0,b>0,,则2a+b的最小值为(
)
A.6
B.
C.
D.
8.勒洛三角形是一种特殊三角形,指分别以正三角形的三个顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形.勒洛三角形的特点是:在任何方向上都有相同的宽度,即能在距离等于其圆弧半径(等于正三角形的边长)的两条平行线间自由转动,并且始终保持与两直线都接触.机械加工业上利用这个性质,把钻头的横截面做成勒洛三角形的形状,就能在零件上钻出正方形的孔来.如在勒洛三角形ABC内随机选取一点,则该点位于正三角形ABC内的概率为(
)
A.
B.
C.
D.
9.若定义域为R的奇函数f(x)满足f(1-x)=f(1+x),且f(3)=2,则f(2021)=(
)
A.2
B.1
C.0
D.-2
10.正四面体P-ABC中,点M是BC的中点,则异面直线PM与AB所成角的余弦值为(
)
A.
B.
C.
D.
11.已知椭圆的右顶点为A,坐标原点为0,若椭圆上存在一点P使得△OAP是等腰直角三角形,则该椭圆的离心率为(
)
A.
B.
C.
D.
12.设若关于x的方程有6个实数解,则实数a的取值范围是(
)
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量a=(2,-1),b=(t,2),若a∥b,则t=
.
14.以双曲线C:的一个焦点为圆心,以5为半径的圆,截该双曲线的一条渐近线所得的弦长为
.
15.已知为锐角,
,则
.
16.某零件的结构是在一个圆锥中挖去了一个正方体,且正方体的一个面与圆锥底面重合,该面所对的面的四个顶点在圆锥侧面内.在图①②③④⑤⑥⑦⑧中选两个分别作为该零件的主视图和俯视图,则所选主视图和俯视图的编号依次可能为
(写出符合要求的一组答案即可).
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
某校计划在秋季运动会期间开展“运动与健康”知识大赛,为此某班开展了10次模拟测试,以此选拔选手代表班级参赛,下表为甲,乙两名学生的历次模拟测试成绩.
场次
1
2
3
4
5
6
7
8
9
10
甲
98
94
97
97
95
93
93
95
93
95
乙
92
94
93
94
95
94
96
97
97
98
甲,乙两名学生测试成绩的平均数分别记作,方差分别记作.
(1)求,;
(2)以这10次模拟测试成绩及(1)中的结果为参考,请你从甲,乙两名学生中选出一人代表班级参加比赛,并说明你作出选择的理由.
18.(12分)
设△ABC的内角A,B,C的对边分别为a,b,c,且c(a+c)=(b-a)(b+a).
(1)求角B;
(2)求sinA+sinC的取值范围.
19.(12分)
如图,多面体
ABCPQ中,QA⊥平面ABC,QA∥PC,点M为PB的中点,AB=BC=AC=PC=2QA=2
(1)求证:QM∥平面ABC;
(2)求三棱锥Q-ABM的体积.
20.(12分)
已知数列的前n项和为,满足.
(1)求数列的通项公式;
(2)记,数列的前n项和为,求证:为定值.
21.(12分)
已知函数.
(1)求函数y=f(x)g(x)的极值;
(2)求证:.
22.(12分)
已知抛物线C:的焦点为F,点O为坐标原点,直线l过点T(4,0)与抛物线C相交于A,B两点(点A位于第一象限).
(1)求证:OA⊥OB;
(2)如图,连接AF,BF并延长分别交抛物线C于点,设直线AB的斜率为,直线,的斜率为,则是否为定值?若是,求出定值;若不是,说明理由.
蚌埠市2022届高三年级第一次教学质量检査考试
数学(文史类)参考答案及评分标准
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
D
C
D
B
A
D
B
C
A
二、填空题:
13.-4
14.8
15.
16.⑤⑦(或①⑧)
三、解答题:
17.(10分)
解:(1),
,………………2分
,
………………6分
(2)答案一:
由(1)可知,,甲,乙两人平均分相同,但甲发挥更稳定,所以可以派甲同学代表班级参赛.…………10分
答案二:
由(1)可知,
,甲,乙两人平均分相同,两人成绩的方差差距不大,但从10次测试成绩的增减趋势可以发现,甲的成绩总体呈下降趋势,乙的成绩总体呈上升趋势,说明乙的状态越来越好,所以可以派乙同学代表班级参赛.………………10分
18.(12分)
解:(1)由题意可得,,
,………………3分
由余弦定理得,即.………………6分
(2)由(1)可知,,
,……………………9分
又,所以,
即的取值范围是.………………12分
19.(12分)
解:(1)取BC中点H,连接MH,AH,由点M为PB的中点,
则MH∥PC且MH=PC,又QA∥PC且QA=PC,
所以,即四边形QAHM为平行四边形,………………3分
从而QM∥AH,而AH平面ABC,QM平面ABC,
所以QM∥平面ABC.……………………6分
(2)由(1)知,MH∥QA,QA平面QAB,MH平面QAB,
所以MH∥平面QAB,则点M到平面QAB的距离与点H到平面QAB的距离相等,即………………9分
由条件知,QA为三棱锥Q-ABH的高,
所以三棱锥Q-ABM的体积.………………12分
20.(12分)
解:(1)当n=1时,
,解得.
当n≥2时,,从而,
化简得,……………………3分
所以数列是首项为2,公比为2的等比数列,
则,即.………………5分
(2),
所以,
从而,
两式相减,得
,………………9分
即,所以,
而,
所以为定值.………………12分
21.(12分)
解:(1)记,定义域为,
则,………………2分
令,解得x=1,
列表如下:
x
(0,1)
1
-
-
0
+
F(x)
单调递减
单调递减
极小值
单调递增
结合表格可知函数y=f(x)g(x)极小值为F(1)=e,无极大值.………………5分
(2).
构造函数,定义域为,
………………8分
当x>0时,;当x<0时,
,
所以G(x)在上单调递减,在上单调递增,………………10分
当时,.
即.………………12分
22.(12分)
解:(1)设直线l方程为,
联立直线l与抛物线C的方程,
消去x,得,
故,又,………………3分
所以,
即.………………5分
(2)设,由焦点F(1,0),
设直线的方程为x=ny+1,
联立直线与抛物线C的方程,
消去x,得,
所以,则
,………………8分
同理可得,,
所以
,
又,所以,即为定值.……………………12分
(以上答案仅供参考,其它解法请参考以上评分标准酌情赋分)
同课章节目录
