2021-2022学年人教版八年级数学上册12.1全等三角形课件(37张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.1全等三角形课件(37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 557.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览






文档简介
(共37张PPT)
12.1
全等三角形
八年级上册
学习目标
1、了解全等三角形的概念、会表示全等三角形,知道全等三角形的对应边、对应角。
2、知道全等三角形的性质。
3、会找全等三角形的对应边、对应角,利用全等三角形性质解简单题。
学习重难点
重点
难点
全等三角形的概念及其基本性质。
能找准全等三角形的对应关系。
1.什么叫全等三角形?
2.你会找全等三角形的对应边、对应角吗?
3.全等三角形有什么性质?
思考
(1)
(2)
(3)
思考
每组的两个图形有什么特点?
观察:
重合
全等形
能够完全重合的两个图形叫做
议一议
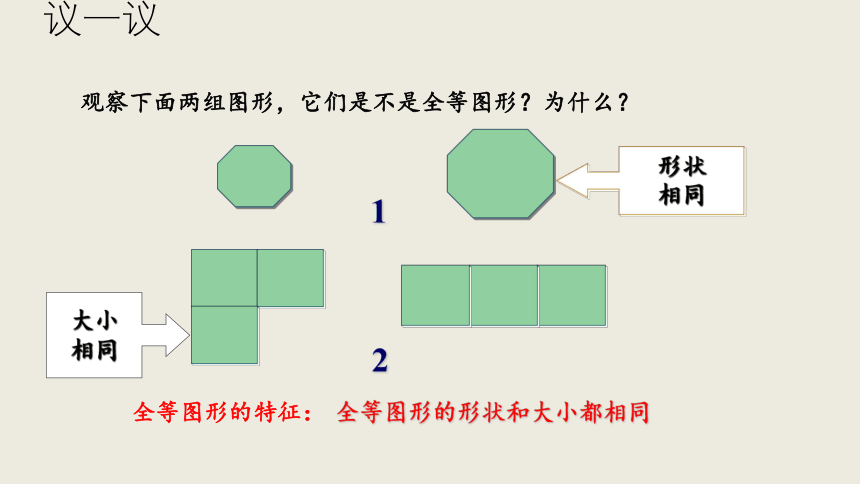
形状
相同
大小
相同
全等图形的特征:
全等图形的形状和大小都相同
观察下面两组图形,它们是不是全等图形?为什么?
1
2
议一议
全等形的分类
分类
同一张底片洗出的照片是能够完全重合的
全等形包括规则图形和不规则图形全等
议一议
A
B
C
E
D
F
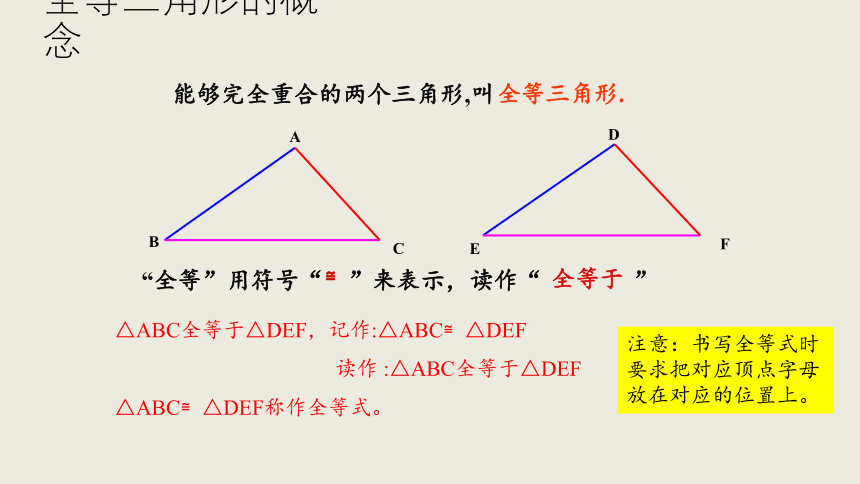
能够完全重合的两个三角形,叫
全等三角形.
注意:书写全等式时要求把对应顶点字母放在对应的位置上。
“全等”用符号“
”来表示,读作“
”
≌
全等于
△ABC全等于△DEF,记作:△ABC≌△DEF
读作
:△ABC全等于△DEF
△ABC≌△DEF称作全等式。
全等三角形的概念
A
B
C
E
F
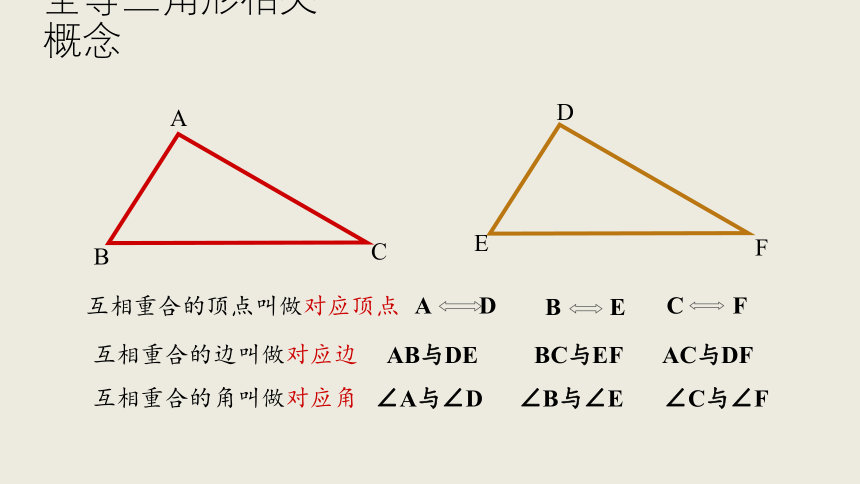
互相重合的边叫做对应边
互相重合的顶点叫做对应顶点
互相重合的角叫做对应角
A
D
B
E
C
F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
D
全等三角形相关概念
(全等三角形的对应角相等)
A
B
C
D
E
F
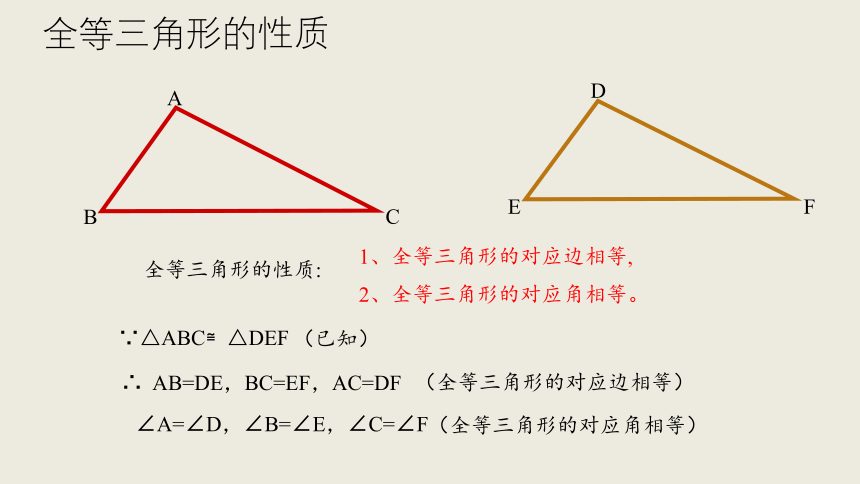
1、全等三角形的对应边相等,
2、全等三角形的对应角相等。
(已知)
(全等三角形的对应边相等)
全等三角形的性质:
∵△ABC≌△DEF
∴
AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的性质
A
B
C
D
E
F
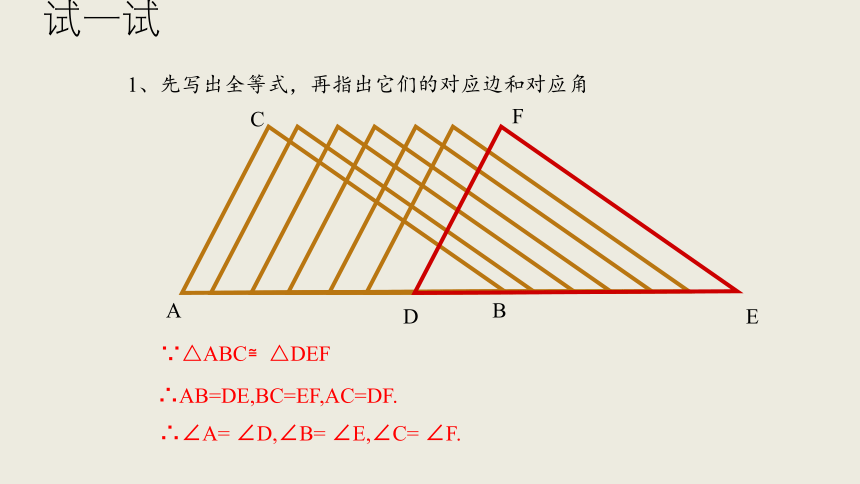
1、先写出全等式,再指出它们的对应边和对应角
∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF.
∴∠A=
∠D,∠B=
∠E,∠C=
∠F.
试一试
B
2、先写出全等式,再指出它们的对应边和对应角
∵△ABC≌△ABD
规律一:有公共边的,公共边是对应边
A
C
D
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD∠C=∠D.
试一试
3、先写出全等式,再指出它们的对应边和对应角
A
C
O
D
B
规律二:有对顶角的,对顶角是对应角
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC=∠BOD.
试一试
A
B
C
D
E
4、先写出全等式,再指出它们的对应边和对应角
∵△ABC≌△ADE
∴AB=AD,AC=AE,BC=DE
∴∠A=∠A,∠B=∠D,∠ACB=∠AED.
规律三:有公共角的,公共角是对应角
试一试
5、先写出全等式,再指出它们的对应边和对应角
∴AB=FD,AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB=
∠FED.
∵△ABC≌△FDE
规律四:一对最大的角是对应角一对最小的角是对应角
A
D
E
B
C
A
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
试一试
找一找:请指出下列全等三角形的对应边和对应角
1、△
ABE≌△ACF
对应角是:
∠A和∠A、∠ABE和∠ACF、
∠AEB和∠AFC;
对应边是:AB和AC、AE和AF、BE和CF。
2、△BCE
≌△CBF
对应角是:∠BCE和∠CBF、∠BEC和∠CFB、∠CBE和∠BCF。
对应边是:CB和BC、CE和BF、CF和BE。
对应角是:
∠BOF和∠COE、∠BFO
和∠CEO、∠
FOB和∠EOC。
对应边是:OF和OE、OB和OC、BF和CE。
说一说
3、△FBO
≌△ECO
1、若ΔDEF≌ΔABC,
∠A=70°,∠B=50°,那么∠F的度数等于(
)
A.50°
B.60°
C.50°
D.以上都不对
B
2、如图,若ΔOAD≌ΔOBC,
且OA=3cm,BD=4cm,BC=6cm,则△OAD周长是
cm.
16
针对训练
3:如图,若ΔABC≌ΔAEF,
AB=AE,∠B=∠E,则下列结论:①AC=AF,
②∠FAB=∠EAB,
③EF=BC,④
∠FAC=∠EAB,其中正确结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
C
针对训练
4:如图,已知ΔABC≌ΔFED,
BC=ED,
求证:AB∥EF
证明:
∵ΔABC≌ΔFED,
BC=ED
∴BC与ED是对应边
∴∠
=∠
,
(
)
∴
AB∥EF
A
F
全等三角形的对应角相等
针对训练
5、如图,已知ΔAEF是ΔABC绕A点顺时针旋转55°得到的,求∠BAE,∠CAF和∠BME的度数.
解:因为AE和AF分别是AB和AC旋转后的位置,
所以∠BAE=∠CAF=
55°;
又因为ΔAEF≌ΔABC,
所以∠B=∠E,
因为∠ANB和∠ENM是对顶角,
所以∠BME=∠BAE=
55°;
针对训练
1、若△ABC与△EDF全等,A和E,B和D分别是对应点,则下列结论错误的是(
)
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF
2、若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为(
)
A.5
B.8
C.7
D.5或8
A
C
课堂练习
3.如图,在直角△OAB中,∠AOB=30°,将△AOB绕点O逆时针方向旋转100°得到△A1OB1,则∠A1OB的度数为_______.
70°
课堂练习
4、如图,△OCA≌△OBD,点C和点B,点A与点D是对应点,则下列结论错误的是(
)
A.∠COA=∠BOD
B.∠A=∠D
C.CA=BD
D.OB=OA
D
C
B
O
A
D
课堂练习
1.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论不一定成立的是( )
A.△ABC≌△DEF
B.∠DEF=90°
C.AC=DF
D.EC=CF
D
应用拓展
2.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为( )
A.12
B.13
C.14
D.15
A
应用拓展
3.如图,Rt△ABE≌Rt△ECD,点B,E,C在同一直线上,则以下结论:①AE=ED;②AE⊥ED;③BC=AB+CD;④AB∥DC.
其中成立的是( )
A.①
B.①③
C.①③④
D.①②③④
D
应用拓展
4.如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
C
应用拓展
5.如图,点A,B,C在一条直线上,△ABD≌△EBC,AB=2
cm,BC=5
cm.
(1)求DE的长.
解:∵△ABD≌△EBC,
∴BD=BC=5
cm,BE=AB=2
cm.
∴DE=BD-BE=3
cm.
应用拓展
(2)
DB与AC垂直吗?为什么?
解:DB与AC垂直.理由如下:
∵△ABD≌△EBC,∴∠ABD=∠EBC.
又∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°.
∴∠EBC=90°,即DB与AC垂直.
应用拓展
6.如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
应用拓展
解:∵△ABC≌△DBE,
∴∠ABC=∠DBE.
∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE.
∴∠CBE=
(∠ABE-∠DBC)=
×(160°-30°)=65°.
(2)若AD=DC=3
cm,BC=4.5
cm,求△DCP与△BPE的周长之和.
解:∵△ABC≌△DBE,
∴BE=BC=4.5
cm,DE=AC=AD+DC=6
cm.
∴△DCP与△BPE的周长之和为
DC+DP+PC+BP+PE+BE
=(DP+PE)+(BP+PC)+DC+BE
=DE+BC+DC+BE
=6+4.5+3+4.5
=18(cm).
应用拓展
7.如图,把两个大小完全相同的长方形堆成“L”形.
(1)指出图中的全等四边形和全等三角形;(2)判断△AFC的形状.
解:(1)四边形ABCD≌四边形AEFG,△AFG≌△FAE≌△ACD≌△CAB.
应用拓展
(2)∵△FAE≌△ACD,∴AF=AC,∠FAE=∠ACD.
∵四边形ABCD是长方形,∴∠ADC=90°,
∴∠ACD+∠CAD=90°.
∴∠FAE+∠CAD=90°,即∠FAC=90°.
∴△AFC是等腰直角三角形.
8.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证BD=DE+CE.
证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE.
∵AE=AD+DE,
∴BD=DE+CE.
应用拓展
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
应用拓展
解:当△ABD满足∠ADB=90°时,BD∥CE.
理由:∵△BAD≌△ACE,∴∠ADB=∠CEA=90°.
易知∠ADB=∠BDE=90°,
∴∠CEA=∠BDE=90°.
∴BD∥CE.
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
寻找对应元素的规律
总结
再
见
12.1
全等三角形
八年级上册
学习目标
1、了解全等三角形的概念、会表示全等三角形,知道全等三角形的对应边、对应角。
2、知道全等三角形的性质。
3、会找全等三角形的对应边、对应角,利用全等三角形性质解简单题。
学习重难点
重点
难点
全等三角形的概念及其基本性质。
能找准全等三角形的对应关系。
1.什么叫全等三角形?
2.你会找全等三角形的对应边、对应角吗?
3.全等三角形有什么性质?
思考
(1)
(2)
(3)
思考
每组的两个图形有什么特点?
观察:
重合
全等形
能够完全重合的两个图形叫做
议一议
形状
相同
大小
相同
全等图形的特征:
全等图形的形状和大小都相同
观察下面两组图形,它们是不是全等图形?为什么?
1
2
议一议
全等形的分类
分类
同一张底片洗出的照片是能够完全重合的
全等形包括规则图形和不规则图形全等
议一议
A
B
C
E
D
F
能够完全重合的两个三角形,叫
全等三角形.
注意:书写全等式时要求把对应顶点字母放在对应的位置上。
“全等”用符号“
”来表示,读作“
”
≌
全等于
△ABC全等于△DEF,记作:△ABC≌△DEF
读作
:△ABC全等于△DEF
△ABC≌△DEF称作全等式。
全等三角形的概念
A
B
C
E
F
互相重合的边叫做对应边
互相重合的顶点叫做对应顶点
互相重合的角叫做对应角
A
D
B
E
C
F
AB与DE
BC与EF
AC与DF
∠A与∠D
∠B与∠E
∠C与∠F
D
全等三角形相关概念
(全等三角形的对应角相等)
A
B
C
D
E
F
1、全等三角形的对应边相等,
2、全等三角形的对应角相等。
(已知)
(全等三角形的对应边相等)
全等三角形的性质:
∵△ABC≌△DEF
∴
AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的性质
A
B
C
D
E
F
1、先写出全等式,再指出它们的对应边和对应角
∵△ABC≌△DEF
∴AB=DE,BC=EF,AC=DF.
∴∠A=
∠D,∠B=
∠E,∠C=
∠F.
试一试
B
2、先写出全等式,再指出它们的对应边和对应角
∵△ABC≌△ABD
规律一:有公共边的,公共边是对应边
A
C
D
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD∠C=∠D.
试一试
3、先写出全等式,再指出它们的对应边和对应角
A
C
O
D
B
规律二:有对顶角的,对顶角是对应角
∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC=∠BOD.
试一试
A
B
C
D
E
4、先写出全等式,再指出它们的对应边和对应角
∵△ABC≌△ADE
∴AB=AD,AC=AE,BC=DE
∴∠A=∠A,∠B=∠D,∠ACB=∠AED.
规律三:有公共角的,公共角是对应角
试一试
5、先写出全等式,再指出它们的对应边和对应角
∴AB=FD,AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB=
∠FED.
∵△ABC≌△FDE
规律四:一对最大的角是对应角一对最小的角是对应角
A
D
E
B
C
A
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
试一试
找一找:请指出下列全等三角形的对应边和对应角
1、△
ABE≌△ACF
对应角是:
∠A和∠A、∠ABE和∠ACF、
∠AEB和∠AFC;
对应边是:AB和AC、AE和AF、BE和CF。
2、△BCE
≌△CBF
对应角是:∠BCE和∠CBF、∠BEC和∠CFB、∠CBE和∠BCF。
对应边是:CB和BC、CE和BF、CF和BE。
对应角是:
∠BOF和∠COE、∠BFO
和∠CEO、∠
FOB和∠EOC。
对应边是:OF和OE、OB和OC、BF和CE。
说一说
3、△FBO
≌△ECO
1、若ΔDEF≌ΔABC,
∠A=70°,∠B=50°,那么∠F的度数等于(
)
A.50°
B.60°
C.50°
D.以上都不对
B
2、如图,若ΔOAD≌ΔOBC,
且OA=3cm,BD=4cm,BC=6cm,则△OAD周长是
cm.
16
针对训练
3:如图,若ΔABC≌ΔAEF,
AB=AE,∠B=∠E,则下列结论:①AC=AF,
②∠FAB=∠EAB,
③EF=BC,④
∠FAC=∠EAB,其中正确结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
C
针对训练
4:如图,已知ΔABC≌ΔFED,
BC=ED,
求证:AB∥EF
证明:
∵ΔABC≌ΔFED,
BC=ED
∴BC与ED是对应边
∴∠
=∠
,
(
)
∴
AB∥EF
A
F
全等三角形的对应角相等
针对训练
5、如图,已知ΔAEF是ΔABC绕A点顺时针旋转55°得到的,求∠BAE,∠CAF和∠BME的度数.
解:因为AE和AF分别是AB和AC旋转后的位置,
所以∠BAE=∠CAF=
55°;
又因为ΔAEF≌ΔABC,
所以∠B=∠E,
因为∠ANB和∠ENM是对顶角,
所以∠BME=∠BAE=
55°;
针对训练
1、若△ABC与△EDF全等,A和E,B和D分别是对应点,则下列结论错误的是(
)
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF
2、若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为(
)
A.5
B.8
C.7
D.5或8
A
C
课堂练习
3.如图,在直角△OAB中,∠AOB=30°,将△AOB绕点O逆时针方向旋转100°得到△A1OB1,则∠A1OB的度数为_______.
70°
课堂练习
4、如图,△OCA≌△OBD,点C和点B,点A与点D是对应点,则下列结论错误的是(
)
A.∠COA=∠BOD
B.∠A=∠D
C.CA=BD
D.OB=OA
D
C
B
O
A
D
课堂练习
1.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论不一定成立的是( )
A.△ABC≌△DEF
B.∠DEF=90°
C.AC=DF
D.EC=CF
D
应用拓展
2.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为( )
A.12
B.13
C.14
D.15
A
应用拓展
3.如图,Rt△ABE≌Rt△ECD,点B,E,C在同一直线上,则以下结论:①AE=ED;②AE⊥ED;③BC=AB+CD;④AB∥DC.
其中成立的是( )
A.①
B.①③
C.①③④
D.①②③④
D
应用拓展
4.如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
C
应用拓展
5.如图,点A,B,C在一条直线上,△ABD≌△EBC,AB=2
cm,BC=5
cm.
(1)求DE的长.
解:∵△ABD≌△EBC,
∴BD=BC=5
cm,BE=AB=2
cm.
∴DE=BD-BE=3
cm.
应用拓展
(2)
DB与AC垂直吗?为什么?
解:DB与AC垂直.理由如下:
∵△ABD≌△EBC,∴∠ABD=∠EBC.
又∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°.
∴∠EBC=90°,即DB与AC垂直.
应用拓展
6.如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
应用拓展
解:∵△ABC≌△DBE,
∴∠ABC=∠DBE.
∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE.
∴∠CBE=
(∠ABE-∠DBC)=
×(160°-30°)=65°.
(2)若AD=DC=3
cm,BC=4.5
cm,求△DCP与△BPE的周长之和.
解:∵△ABC≌△DBE,
∴BE=BC=4.5
cm,DE=AC=AD+DC=6
cm.
∴△DCP与△BPE的周长之和为
DC+DP+PC+BP+PE+BE
=(DP+PE)+(BP+PC)+DC+BE
=DE+BC+DC+BE
=6+4.5+3+4.5
=18(cm).
应用拓展
7.如图,把两个大小完全相同的长方形堆成“L”形.
(1)指出图中的全等四边形和全等三角形;(2)判断△AFC的形状.
解:(1)四边形ABCD≌四边形AEFG,△AFG≌△FAE≌△ACD≌△CAB.
应用拓展
(2)∵△FAE≌△ACD,∴AF=AC,∠FAE=∠ACD.
∵四边形ABCD是长方形,∴∠ADC=90°,
∴∠ACD+∠CAD=90°.
∴∠FAE+∠CAD=90°,即∠FAC=90°.
∴△AFC是等腰直角三角形.
8.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证BD=DE+CE.
证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE.
∵AE=AD+DE,
∴BD=DE+CE.
应用拓展
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
应用拓展
解:当△ABD满足∠ADB=90°时,BD∥CE.
理由:∵△BAD≌△ACE,∴∠ADB=∠CEA=90°.
易知∠ADB=∠BDE=90°,
∴∠CEA=∠BDE=90°.
∴BD∥CE.
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
寻找对应元素的规律
总结
再
见
