2021年浙江省普通高中学业水平合格性考试数学仿真模拟卷(2)(PDF版无答案)
文档属性
| 名称 | 2021年浙江省普通高中学业水平合格性考试数学仿真模拟卷(2)(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 265.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 07:29:58 | ||
图片预览

文档简介
2021年浙江省普通高中学业水平合格性考试数学仿真模拟卷
选择题(本大题共18小题,每小题3分,共54分。每小题列出的四个选项中只
个是符合题目要求的,不选,多选,错选均不给分。)
知集
2.函数f(x)=√x+3+
定义域
算3
4.经过坐标原
坐标为
般
体的体积为
E视图
侧视图
您视图
8
16元
在
定义运算
:a
2a+b,则满足x
(x-2)<0的解集为
第1页
设实数x,y满足约束条件3x+-6>0,则y的最大值是(
y
点P(
线2x
线的方程
角A
C所对的边分别是a、b、c,若b
ABC的形状
A.等腰三角
B.等边三角形
C.锐角三角形
钝角三角形
知直线
不同的平面a
命题正确的是
角a终边上有
必要不充分条件
充分不必要条
C.充要条仁
D.既不充分也不必要条
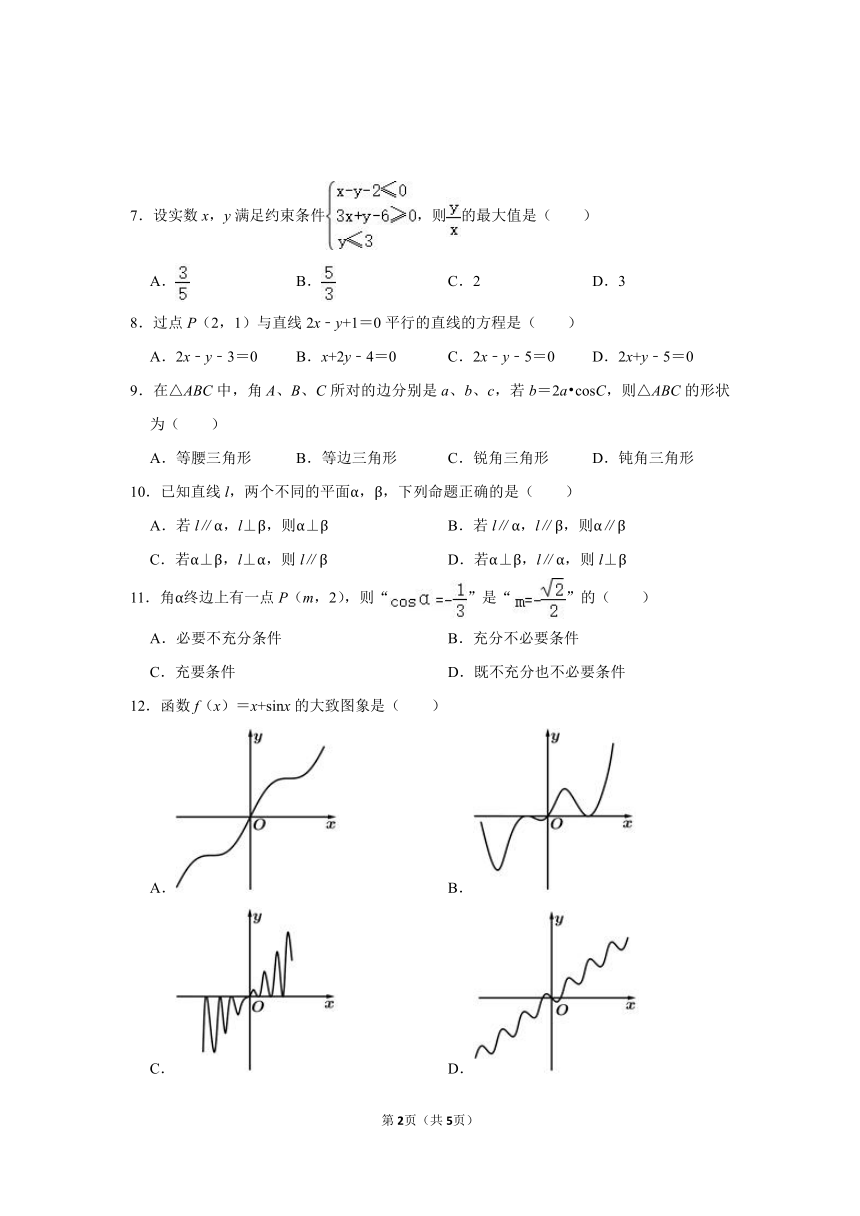
函数f
致图象是()
O
第2页
知等差数列{a
项和为S,若—°11
11
4.如图
ABCD的对角线AC
N分别为A
且异面直线AC
所成的角为
D
知a,b是单位向量,且a+b=(1,-1),若向量c=a-b,则a与c的夹角为
2
知函数f(
函数,满足∫
f(-x),且当
),则函数y=f(x)-x3的零点个数是()
圆的方程为x+y。=1(a>b>0),F1、F2为椭
右焦
为椭圆上在第
为△PF1F
该椭圆
的离心率为
长为2的正方体ABCD-A1B1C1D
E在棱AA
AE=3A1E,点G是棱
点,点F
入BB1(0角的余
时,经过
点的截
积为(
A.26
√17
7√6
填空题(本大题共4小题,每空3分,共15分。)
设S为等比数列{a
20.已知向量a=(2,t),b=(-1,2),且a∥b,则
知梯形
CD=4,3A=2EC,若双曲线以A、B为焦
双曲线
为
y=(1g2x)2+(t-2)10g2xt+1,若
取值范围
解答题(本大题共3小题,共31分.)
知函数f(x)=cos(x)-2
求f(0)的值
求函数f(x)的最
期
(Ⅲ)求函数f(x)的最大
到最大
集
知抛物线C:y2
(p>0)的焦点为F,点A(4,m)在抛物线
l△OAF
的面积为1。2(O为坐标原点
(1)求抛物线C的方程
线
抛物线C交于M,N两点,若OM⊥ON,求直线l的方程
函数f(
最小值m的值
(2)在
知
数
不等式19
成立,求实数t的取值范
g(x)=x(f(x)-|x|-2)
时
等式
成
实数t的最大值及
的值
选择题(本大题共18小题,每小题3分,共54分。每小题列出的四个选项中只
个是符合题目要求的,不选,多选,错选均不给分。)
知集
2.函数f(x)=√x+3+
定义域
算3
4.经过坐标原
坐标为
般
体的体积为
E视图
侧视图
您视图
8
16元
在
定义运算
:a
2a+b,则满足x
(x-2)<0的解集为
第1页
设实数x,y满足约束条件3x+-6>0,则y的最大值是(
y
点P(
线2x
线的方程
角A
C所对的边分别是a、b、c,若b
ABC的形状
A.等腰三角
B.等边三角形
C.锐角三角形
钝角三角形
知直线
不同的平面a
命题正确的是
角a终边上有
必要不充分条件
充分不必要条
C.充要条仁
D.既不充分也不必要条
函数f
致图象是()
O
第2页
知等差数列{a
项和为S,若—°11
11
4.如图
ABCD的对角线AC
N分别为A
且异面直线AC
所成的角为
D
知a,b是单位向量,且a+b=(1,-1),若向量c=a-b,则a与c的夹角为
2
知函数f(
函数,满足∫
f(-x),且当
),则函数y=f(x)-x3的零点个数是()
圆的方程为x+y。=1(a>b>0),F1、F2为椭
右焦
为椭圆上在第
为△PF1F
该椭圆
的离心率为
长为2的正方体ABCD-A1B1C1D
E在棱AA
AE=3A1E,点G是棱
点,点F
入BB1(0
时,经过
点的截
积为(
A.26
√17
7√6
填空题(本大题共4小题,每空3分,共15分。)
设S为等比数列{a
20.已知向量a=(2,t),b=(-1,2),且a∥b,则
知梯形
CD=4,3A=2EC,若双曲线以A、B为焦
双曲线
为
y=(1g2x)2+(t-2)10g2xt+1,若
取值范围
解答题(本大题共3小题,共31分.)
知函数f(x)=cos(x)-2
求f(0)的值
求函数f(x)的最
期
(Ⅲ)求函数f(x)的最大
到最大
集
知抛物线C:y2
(p>0)的焦点为F,点A(4,m)在抛物线
l△OAF
的面积为1。2(O为坐标原点
(1)求抛物线C的方程
线
抛物线C交于M,N两点,若OM⊥ON,求直线l的方程
函数f(
最小值m的值
(2)在
知
数
不等式19
成立,求实数t的取值范
g(x)=x(f(x)-|x|-2)
时
等式
成
实数t的最大值及
的值
同课章节目录
