高中数学人教A版(2019)选择性必修第一册第一章1.2空间向量基本定理(1)-课件(共41张PPT))
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第一章1.2空间向量基本定理(1)-课件(共41张PPT)) |  | |
| 格式 | zip | ||
| 文件大小 | 478.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 09:45:23 | ||
图片预览





文档简介
(共41张PPT)
空间向量基本定理(1)
如果
e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
若
e1,e2不共线,我们把{e1,e2}叫做表示这一平面内所有向量的一个基底.
平面向量基本定理
问题1
空间中的任意向量能不能通过有限个向量的线性运算来表示呢?
追问2
两个不共线的向量还够用吗?
如果两个向量
a,b
不共线,那么向量
p
与向量
a,b
共面的充要条件是存在唯一的有序实数对
(x,y),使
p=xa+yb.
至少需要三个向量.
追问1
为了表示空间中的任意向量,我们至少需要几个向量?
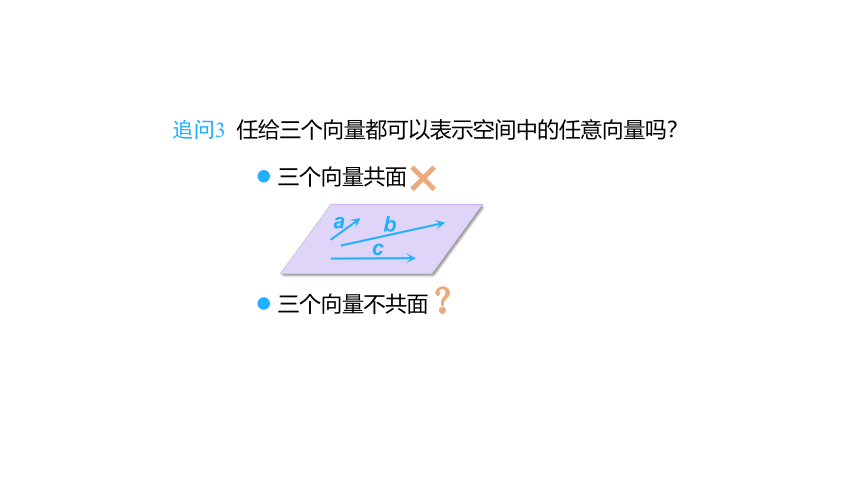
三个向量共面
三个向量不共面
a
b
c
追问3
任给三个向量都可以表示空间中的任意向量吗?
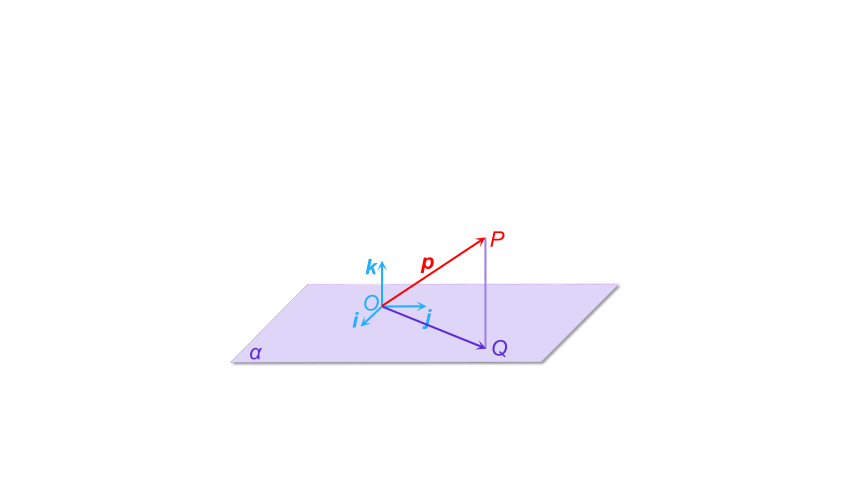
?
p
i
j
k
P
Q
O
α
xi
p
i
j
k
P
Q
O
yj
zk
α
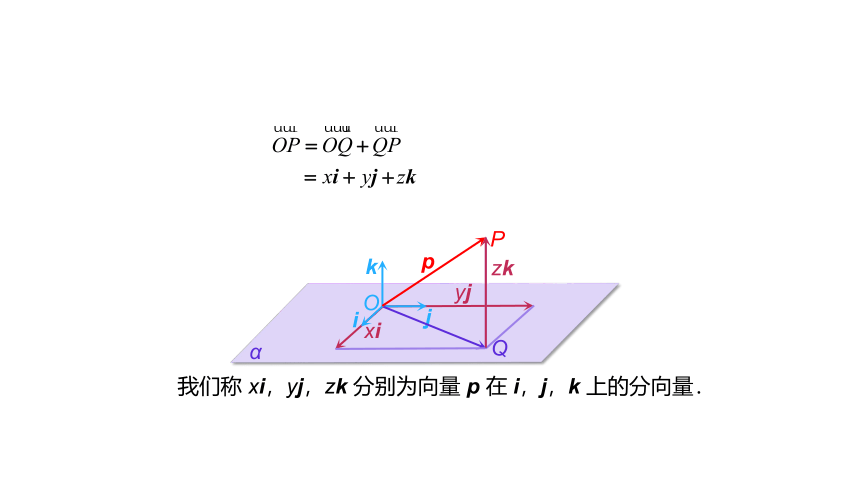
我们称
xi,yj,zk
分别为向量
p
在
i,j,k
上的分向量.
xi
p
i
j
k
P
Q
O
yj
zk
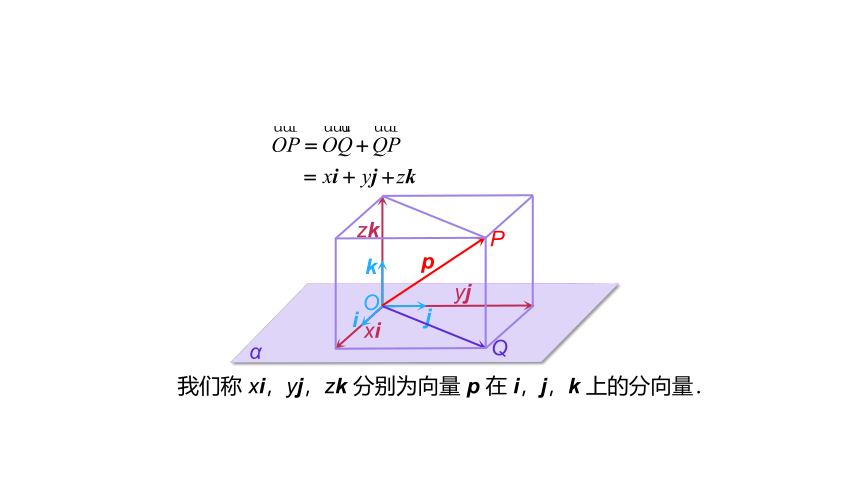
我们称
xi,yj,zk
分别为向量
p
在
i,j,k
上的分向量.
α
追问4
如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗
?
a
b
c
p
a
b
c
O
P
α
p
a
c
b
B
C
A
Q
Q
α
a
b
c
O
P
p
a
c
b
B
C
A
O
Q
P
p
a
c
b
B
C
A
α
a
b
c
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
问题2
你能类比平面向量基本定理的表述,写出空间向量基本定理吗?
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
那么,所有空间向量组成的集合就是
{
p
|
p=xa+yb+zc,x,y,z∈R}.
空间向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
我们把{a,b,c}叫做空间的一个基底(base),a,b,c
都叫做基向量(base
vectors).
问题3
空间的基底有多少个,需要满足什么条件?
答:任意三个不共面的向量都能构成空间的一个基底.
空间的基底有无穷多个.
{a,b,c}是空间的一个基底,当且仅当
a,b,c不共面.
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用{i,j,k}表示.
i
j
k
O
a
i
j
k
P
Q
O
由空间向量基本定理可知,对空间中的任意向量
a,均可以分解为三个向量
xi,yj,zk,使
a=xi+yj+zk.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{e1,e2}
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{a,b,c}
{e1,e2}
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{a,b,c}
{e1,e2}
二维
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{a,b,c}
{e1,e2}
二维
三维
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
{a,b,c}
{e1,e2}
二维
三维
一维
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
{a,b,c}
{e1,e2}
二维
三维
一维
{a}
空间向量基本定理
平面向量基本定理
向量共线充要条件
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
向量
a
(
a
≠
0)与向量
b共线的充要条件是:存在唯一一个实数
λ,使
b=λa.
{a,b,c}
{e1,e2}
二维
三维
一维
{a}
给我一个支点,我可以撬起地球.
——阿基米德
给我一个基底,
我还你一个空间!
1.
如图,已知平行六面体OABC-O′A′B′C′,点G是侧面BB′C′C的中心,且
(1)
{a,b,c}是否构成空间的一个基底?
(2)
如果{a,b,c}构成空间的一个基底,
那么用它表示下列向量:
课后作业
2.已知四面体
OABC,M,N
分别是边
OA,BC的中点,且
,用a,b,c表示向量
空间向量基本定理(1)
如果
e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
若
e1,e2不共线,我们把{e1,e2}叫做表示这一平面内所有向量的一个基底.
平面向量基本定理
问题1
空间中的任意向量能不能通过有限个向量的线性运算来表示呢?
追问2
两个不共线的向量还够用吗?
如果两个向量
a,b
不共线,那么向量
p
与向量
a,b
共面的充要条件是存在唯一的有序实数对
(x,y),使
p=xa+yb.
至少需要三个向量.
追问1
为了表示空间中的任意向量,我们至少需要几个向量?
三个向量共面
三个向量不共面
a
b
c
追问3
任给三个向量都可以表示空间中的任意向量吗?
?
p
i
j
k
P
Q
O
α
xi
p
i
j
k
P
Q
O
yj
zk
α
我们称
xi,yj,zk
分别为向量
p
在
i,j,k
上的分向量.
xi
p
i
j
k
P
Q
O
yj
zk
我们称
xi,yj,zk
分别为向量
p
在
i,j,k
上的分向量.
α
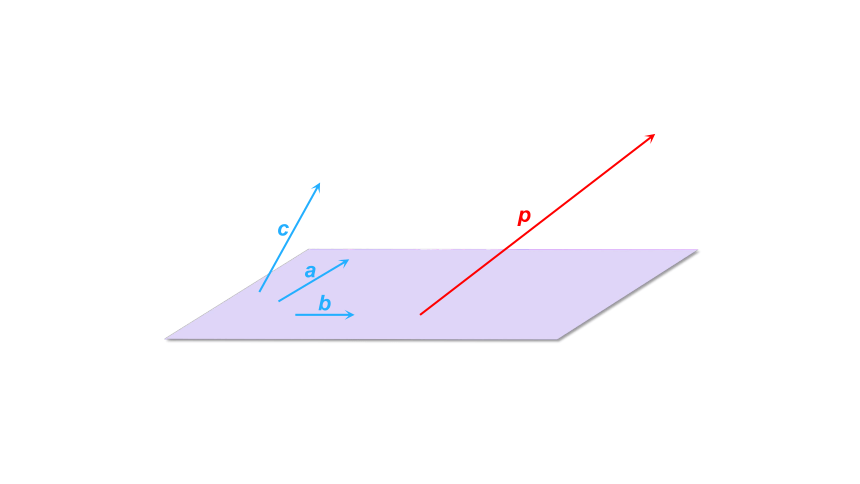
追问4
如果给定的三个不共面的向量不是两两垂直的,能用它们的线性运算表示任意一个空间向量吗
?
a
b
c
p
a
b
c
O
P
α
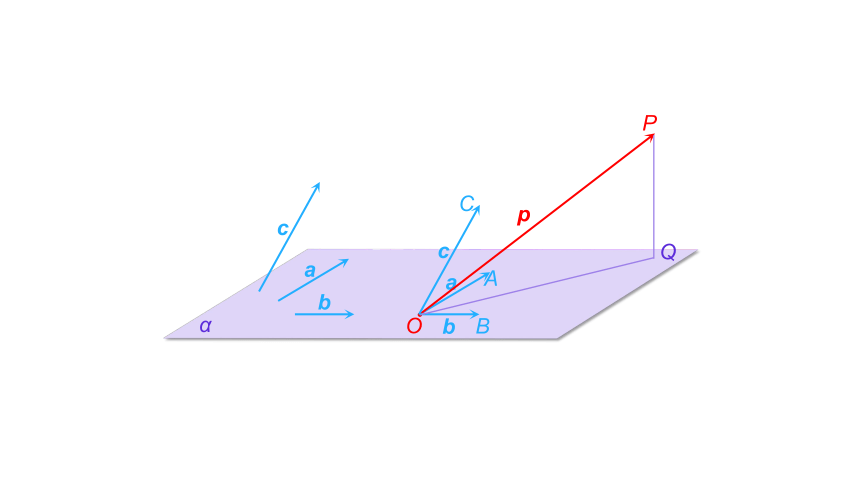
p
a
c
b
B
C
A
Q
Q
α
a
b
c
O
P
p
a
c
b
B
C
A
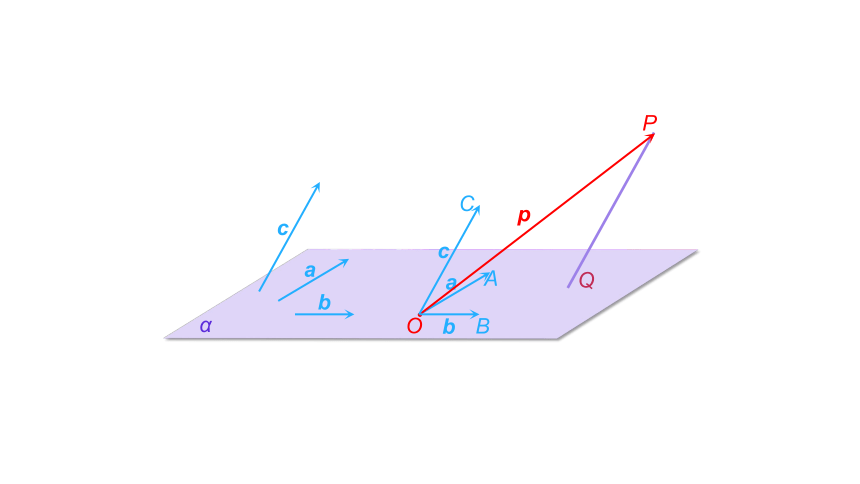
O
Q
P
p
a
c
b
B
C
A
α
a
b
c
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
xa
O
Q
P
p
a
c
b
yb
zc
B
C
A
α
a
b
c
问题2
你能类比平面向量基本定理的表述,写出空间向量基本定理吗?
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
空间向量基本定理
平面向量基本定理
如果
e1,e2
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
a,有且只有一对实数
λ1,λ2,使
a=λ1e1+λ2e2.
那么,所有空间向量组成的集合就是
{
p
|
p=xa+yb+zc,x,y,z∈R}.
空间向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
我们把{a,b,c}叫做空间的一个基底(base),a,b,c
都叫做基向量(base
vectors).
问题3
空间的基底有多少个,需要满足什么条件?
答:任意三个不共面的向量都能构成空间的一个基底.
空间的基底有无穷多个.
{a,b,c}是空间的一个基底,当且仅当
a,b,c不共面.
特别地,如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用{i,j,k}表示.
i
j
k
O
a
i
j
k
P
Q
O
由空间向量基本定理可知,对空间中的任意向量
a,均可以分解为三个向量
xi,yj,zk,使
a=xi+yj+zk.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{e1,e2}
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{a,b,c}
{e1,e2}
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{a,b,c}
{e1,e2}
二维
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
问题4
平面向量基本定理与空间向量基本定理的联系与区别是什么?
{a,b,c}
{e1,e2}
二维
三维
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
{a,b,c}
{e1,e2}
二维
三维
一维
空间向量基本定理
平面向量基本定理
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
{a,b,c}
{e1,e2}
二维
三维
一维
{a}
空间向量基本定理
平面向量基本定理
向量共线充要条件
如果三个向量
a,b,c
不共面,那么对任意一个空间向量
p,存在唯一的有序实数组
(x,y,z),使得
p=xa+yb+zc.
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使
a=λ1e1+λ2e2.
向量
a
(
a
≠
0)与向量
b共线的充要条件是:存在唯一一个实数
λ,使
b=λa.
{a,b,c}
{e1,e2}
二维
三维
一维
{a}
给我一个支点,我可以撬起地球.
——阿基米德
给我一个基底,
我还你一个空间!
1.
如图,已知平行六面体OABC-O′A′B′C′,点G是侧面BB′C′C的中心,且
(1)
{a,b,c}是否构成空间的一个基底?
(2)
如果{a,b,c}构成空间的一个基底,
那么用它表示下列向量:
课后作业
2.已知四面体
OABC,M,N
分别是边
OA,BC的中点,且
,用a,b,c表示向量
