探索三角形全等(3)

(共22张PPT)
学习目标：
1、在掌握三角形全等的“边边边”“角边角”“角角边”的条件，继续探索、经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程.
2、能探索出三角形全等的“边角边”的条件.
3、能够进行有条理的思考进行简单的推理.
学习重点：理解两边和它们的夹角对应相等的两个三角形全等的条件。
学习难点：有条理的思考和进行推理：应用“SAS”去判断三角形全等
回顾与思考
到目前为止，我们已学过哪些方法判定两三角形全等？
答：边边边（SSS）角边角（ASA）角角边（AAS）
根据探索三角形全等的条件，至少需要三个条件，除了上述三种情况外，还有哪种情况？
答：两边一角相等
那么有几种可能的情况呢？
答：两边及夹角或两边及其一边的对角
一）自主探索并解决下列问题：
1、如果已知一个三角形的两边及一角，那么有几种可能的情况呢？
.
2、如果“两边及一角”条件中的角是两边的夹角，比如三角形两边分别为3cm，5cm，它们所夹的角为60°，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？动手试一试.
有两种情况：两边及其中一边对的角（SSA）和
两边与其夹角（SAS）
全等
自主合作（做一做）
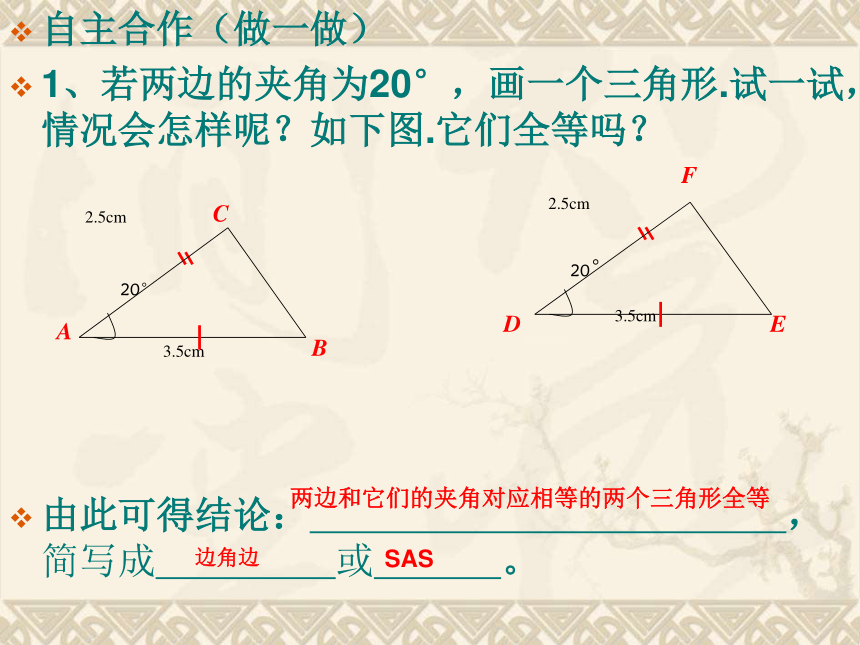
1、若两边的夹角为20°，画一个三角形.试一试，情况会怎样呢？如下图.它们全等吗？
由此可得结论： ，简写成 或 。
3.5cm
2.5cm
20°
A
B
C
3.5cm
2.5cm
20°
E
F
D
两边和它们的夹角对应相等的两个三角形全等
边角边
SAS
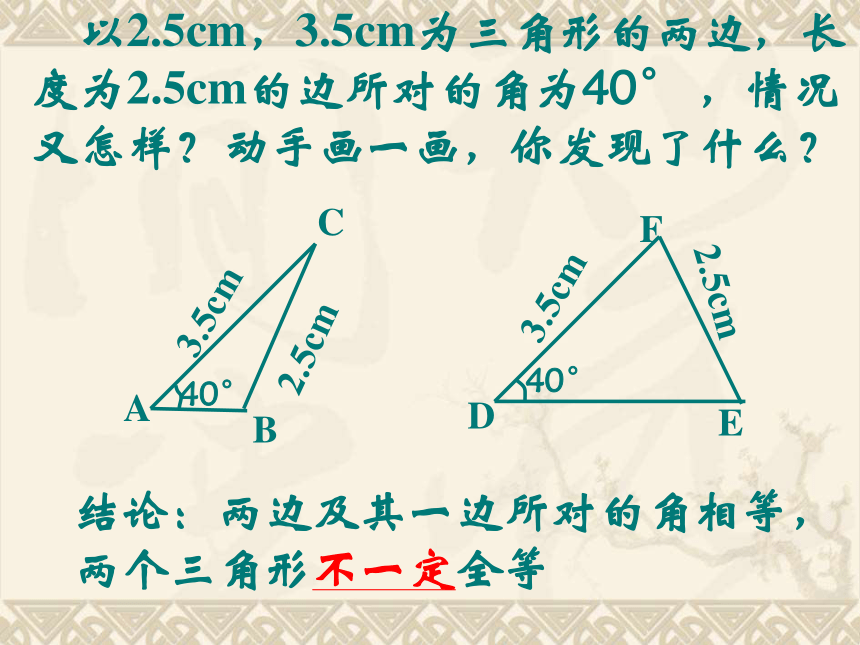
以2.5cm，3.5cm为三角形的两边，长度为2.5cm的边所对的角为40° ，情况又怎样？动手画一画，你发现了什么？
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论：两边及其一边所对的角相等，两个三角形不一定全等
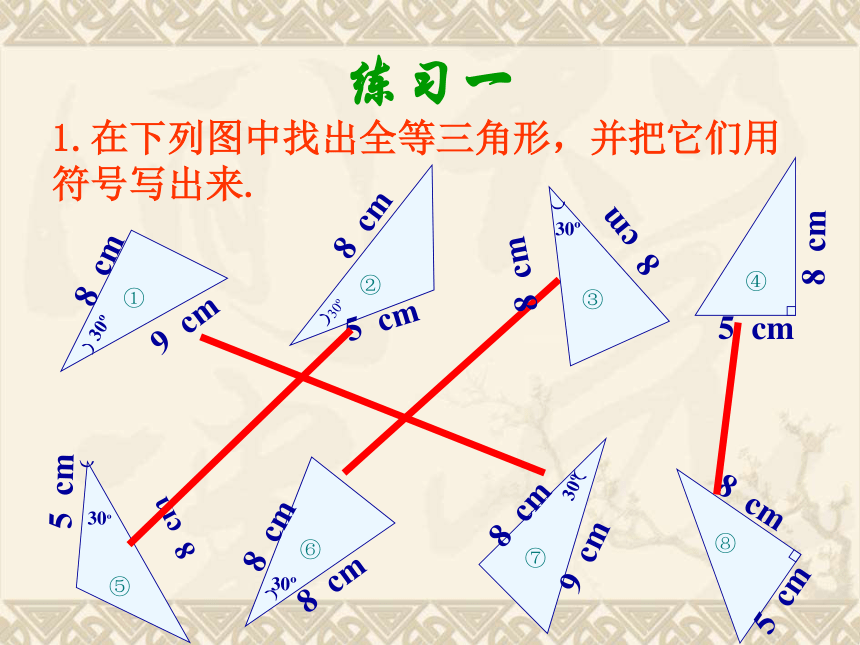
1.在下列图中找出全等三角形，并把它们用
符号写出来.
①

30
8 cm
9 cm
⑥

30
8 cm
8 cm
Ⅳ
④
8 cm
5 cm
②
30

8 cm
5 cm
⑤
30
8 cm

5 cm
⑧
8 cm
5 cm

30
8 cm
9 cm
⑦
Ⅲ

30
8 cm
8 cm
③
练习一
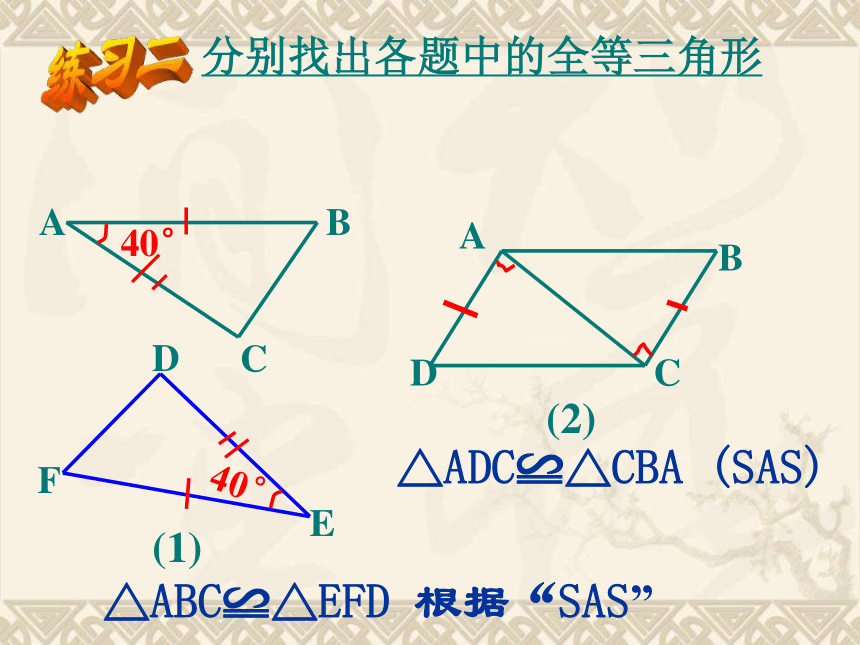
分别找出各题中的全等三角形
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD 根据“SAS”
△ADC≌△CBA (SAS)
自主尝试：完成下面的推理：
如图，已知AD∥BC，AD=BC.试说明：
（1）AB=DC，（2）AB∥DC.
证明：∵AD∥BC（ ）
∴___ ______( )
∴△ADB≌△CBD（ ）
∴AB=DC（ ）
∠ABD=_________（ ）
∴AB∥CD（ ）
∠1=∠2
已知
两直线平行内错角相等
BC
∠1
∠2
BD
BD
SAS
全等三角形对应边相等
∠CDB
全等三角形对应角相等
内错角相等两直线平行
B
C
D
E
A
例1 如图，已知AB＝AC，AD＝AE。∠B与∠C相等吗？为什么？
C
E
A
B
A
D
解：∠B＝∠C 理由如下： 在△ABD和△ACE中
∴△ABD≌△ACE（SAS）
∴∠B＝∠C（全等三角形
对应角相等）
因此 ∠B＝∠C
F
E
D
C
B
A
例2 如图，∠B＝∠E，AB＝EF，BD＝EC，那么△ABC与　△FED全等吗？为什么？
解：△ABC≌△FED
理由如下 ∵BD=EC
∴BD－CD＝EC－CD 即BC＝ED 　　
在△ABC与△FED中
∴△ABC≌△FED（SAS）
因此△ABC≌△FED
　



í
ì


（已知）
＝
（已知）
＝
（已知）
＝
ED
BC
C
B
EF
AB
AC∥FD吗？为什么？
小明做了一个如图所示的风筝，其中∠EDH=∠FDH, ED=FD ，将上述条件标注在图中，小明不用测量就能知道EH=FH吗？与同桌进行交流。
E
F
D
H
小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。
AC=DC
∠ACB=∠DCE
BC=EC
△ACB≌△DCE(SAS)
AB=DE
E
C
B
A
D
如图线段AB是一个池塘的长度，
现在想测量这个池塘的长度，在
水上测量不方便，你有什么好的
方法较方便地把池塘的长度测量
出来吗？想想看。
2、在△ABC中，AB=AC，AD是∠BAC的角平分线.那么BD＝CD吗？
1
2
A
B
C
D
3、如图：已知AB＝AC，∠B＝∠C，
△ABD与△ACE全等吗？为什么？
B
C
D
E
A
4、如图，E，F在BC上，BE=CF，AB=CD，AB∥CD.
试说明：（1）⊿ABF≌ ⊿DCE； （2）AF∥DE
A
B
C
D
E
F
5、如图，若AB=AD，BC=DE， ∠B=∠ADE.
试说明：（1）AC=AE，（2）∠EDC =∠EAF.
1.若AB=AC，则添加什么条件可得△ABD≌ △ACD
△ABD≌ △ACD
AD=AD
AB=AC
A
B
D
C
∠BAD= ∠CAD
S
A
S
练习二
2.已知如图，点D 在AB上，点E在AC上，BE与CD交于点O，
△ABE≌ △ACD
S
A
S
AB=AC
∠A= ∠ A
AD=AE
要证△ABE≌ △ACD需添加什么条件
B
E
A
A
C
D
O
2.已知如图，点D 在AB上，点E在AC上，BE与CD交于点O，
S
A
S
OB=OC
∠BOD= ∠ COE
OD=OE
要证△BOD≌ △COE需添加什么条件
B
E
A
A
C
D
O
△BOD≌ △COE
谈谈你本节课的收获是什么？