2020-2021学年黑龙江省哈尔滨市松北区七年级(下)期末数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市松北区七年级(下)期末数学试卷(word解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 409.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 00:00:00 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市松北区七年级(下)期末数学试卷(五四学制)
一、选择题(每小题3分,共计30分)
1.(3分)下列方程中,是二元一次方程的是( )
A.2x+=8
B.﹣x2+2y=7
C.﹣x+2=9
D.7x﹣2y=13
2.(3分)如果x>y,则下列变形中正确的是( )
A.﹣xy
B.y
C.3x>5y
D.x﹣3>y﹣3
3.(3分)下列长度的三条线段中,能组成三角形的是( )
A.2cm,5cm,7cm
B.0.1cm,0.1cm,0.1cm
C.8cm,8cm,17cm
D.7cm,40cm,8cm
4.(3分)把不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
5.(3分)下列四个图形中,线段BE是△ABC的高的图形是( )
A.
B.
C.
D.
6.(3分)一个凸n边形,其每个内角都是140°,则n的值为( )
A.6
B.7
C.8
D.9
7.(3分)如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠使点A落在BC边上的点A′处,折痕为CD,则∠A′DC=( )
A.10°
B.30°
C.65°
D.85°
8.(3分)若不等式(k﹣2)x>k﹣2的解集是x<1,则k满足( )
A.k<0
B.k>2
C.k<2
D.k<﹣2
9.(3分)足球比赛的得分规则如下:胜一场得3分,平一场得1分,负一场得0分.某足球队一共进行了14场比赛,其中负了5场,共得19分.设该球队胜了x场,平了y场,依题意可列方程组( )
A.
B.
C.
D.
10.(3分)有下列说法:
(1)外角和为360°的多边形一定是三角形;
(2)有两条边分别相等的两个三角形是全等三角形;
(3)角的平分线上的点到角的两边的距离相等;
(4)如果∠A=∠B+∠C,那么△ABC是直角三角形.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共计30分)
11.(3分)已知4x﹣2y=3,用含x的代数式表示y,则y=
.
12.(3分)x的3倍与7的和大于9,用不等式可表示为
.
13.(3分)甲、乙两台机床生产一种零件,10天中两台机床每天生产次品的平均数都是2,方差是S甲2=0.76,S乙2=1.65,两台机床出次品的波动较小的是
机床.(填“甲”或“乙”)
14.(3分)若是关于x、y的方程kx﹣2y=2的一个解,则k=
.
15.(3分)某公司招聘员工,公司对应聘人员进行三项测试:语言、设计和综合知识.公司将把三项测试得分按2:3:4的比确定每人的最后成绩,已知小王三项测试得分依次为90分、81分和72分,则他的最后成绩为
分.
16.(3分)一个等腰三角形的两边长分别为3和7,这个三角形的周长是
.
17.(3分)如图,∠ABD=15°,∠ACD=30°,∠A=45°,则∠BDC的度数为
°.
18.(3分)某次知识竞赛共有20题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少答对
道.
19.(3分)已知AH为△ABC的高,若∠B=40°,∠ACH=65°,则∠BAC的度数为
°.
20.(3分)如图,在△ABC中,点D为AC边的中点,过点C作CF∥AB,过点D作直线EF交AB于点E,交直线CF于点F,若BE=9,CF=6,△ABC的面积为50,则△CDF的面积为
.
三、解答题(21-25每题各8分,26,27题各10分)
21.(8分)解下列方程组及不等式组:
(1);
(2).
22.(8分)如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC的边BC上的高AD;
(2)画出△ABC的边AC上的中线BE;
(3)直接写出△ABE的面积为
.
23.(8分)为了调查学生每天零花钱情况,对我校七年级某班50名同学每天零花钱情况进行了统计,并绘制成下面的统计图:
(1)这50名同学零花钱的众数为
;中位数为
;
(2)求这50名同学零花钱的平均数;
(3)该校共有学生3000人,请你根据该班的零花钱情况,估计这所中学学生每天的零花钱总数是多少元?
24.(8分)如图,在△ABC中,AB=AC,BE⊥AC于点E,CF⊥AB于点F,且BE与CF相交于点O.
(1)求证:BF=CE;
(2)不添加辅助线,直接写出图中所有的全等三角形.
25.(8分)学校为丰富学生的业余生活,为学生购买排球和篮球.若买10个排球和8个篮球需1600元;若买15个排球和20个篮球需3200元.
(1)每个排球和篮球的售价分别多少元?
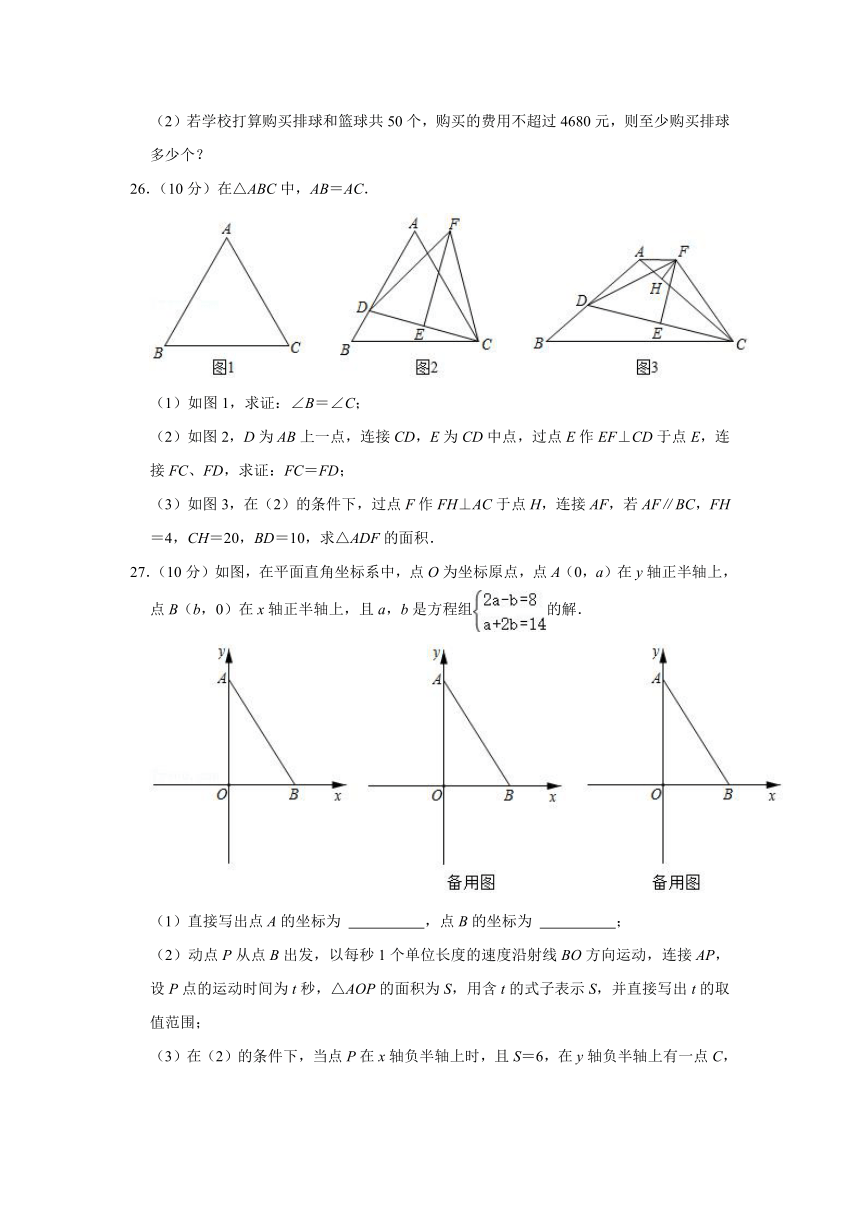
(2)若学校打算购买排球和篮球共50个,购买的费用不超过4680元,则至少购买排球多少个?
26.(10分)在△ABC中,AB=AC.
(1)如图1,求证:∠B=∠C;
(2)如图2,D为AB上一点,连接CD,E为CD中点,过点E作EF⊥CD于点E,连接FC、FD,求证:FC=FD;
(3)如图3,在(2)的条件下,过点F作FH⊥AC于点H,连接AF,若AF∥BC,FH=4,CH=20,BD=10,求△ADF的面积.
27.(10分)如图,在平面直角坐标系中,点O为坐标原点,点A(0,a)在y轴正半轴上,点B(b,0)在x轴正半轴上,且a,b是方程组的解.
(1)直接写出点A的坐标为
,点B的坐标为
;
(2)动点P从点B出发,以每秒1个单位长度的速度沿射线BO方向运动,连接AP,设P点的运动时间为t秒,△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)在(2)的条件下,当点P在x轴负半轴上时,且S=6,在y轴负半轴上有一点C,过点B作x轴垂线,与射线PC交于点D,若∠CPO+2∠APO=180°,PD=,连接AD,交OB于点E,求点E的坐标.
2020-2021学年黑龙江省哈尔滨市松北区七年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.(3分)下列方程中,是二元一次方程的是( )
A.2x+=8
B.﹣x2+2y=7
C.﹣x+2=9
D.7x﹣2y=13
【分析】根据二元一次方程的定义即可求出答案.
【解答】解:A、该方程不是整式方程,故不符合题意.
B、该方程中含有两个未知数,但未知数的最高次数是2,不是二元一次方程,故不符合题意.
C、该方程是一元一次方程,故不符合题意.
D、该方程属于二元一次方程,故不符合题意.
故选:D.
2.(3分)如果x>y,则下列变形中正确的是( )
A.﹣xy
B.y
C.3x>5y
D.x﹣3>y﹣3
【分析】根据不等式的性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变.不等式两边乘(或除以)同一个负数,不等号的方向改变.
【解答】解:A、两边都乘以﹣,故A错误;
B、两边都乘以,故B错误;
C、左边乘3,右边乘5,故C错误;
D、两边都减3,故D正确;
故选:D.
3.(3分)下列长度的三条线段中,能组成三角形的是( )
A.2cm,5cm,7cm
B.0.1cm,0.1cm,0.1cm
C.8cm,8cm,17cm
D.7cm,40cm,8cm
【分析】看哪个选项中两条较小的边的和大于最大的边即可.
【解答】解:A、2+5=7,不能构成三角形;
B、0.1+0.1>0.1,能构成三角形;
C、8+8<17,不能构成三角形;
D、7+8<40,不能构成三角形.
故选:B.
4.(3分)把不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
【分析】分别把两条不等式解出来,然后判断哪个选项表示的正确.
【解答】解:由(1)得:x≥﹣1,
由(2)得:x<2,
所以﹣1≤x<2.
故选:C.
5.(3分)下列四个图形中,线段BE是△ABC的高的图形是( )
A.
B.
C.
D.
【分析】根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解答】解:线段BE是△ABC的高的图是选项A.
故选:A.
6.(3分)一个凸n边形,其每个内角都是140°,则n的值为( )
A.6
B.7
C.8
D.9
【分析】根据多边形每个内角与其相邻的内角互补,则正n边形的每个外角的度数=180°﹣140°=40°,然后根据多边形的外角和为360°即可得到n的值.
【解答】解:∵正n边形的每个内角都是140°,
∴正n边形的每个外角的度数=180°﹣140°=40°,
∴n==9.
故选:D.
7.(3分)如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠使点A落在BC边上的点A′处,折痕为CD,则∠A′DC=( )
A.10°
B.30°
C.65°
D.85°
【分析】根据翻折变换的性质可得∠A′DC=∠ADC,CD是角平分线,然后根据三角形的内角和列式计算即可得解.
【解答】解:∵折叠后点A落在边CB上A′处,∠ACB=90°
∴折痕CD是角平分线,
∴∠A′CD=∠ACD=45°
又∵∠A=50°,
∴∠A′DC=∠ADC=180°﹣∠A﹣∠ACD=180°﹣50°﹣45°=85°.
故选:D.
8.(3分)若不等式(k﹣2)x>k﹣2的解集是x<1,则k满足( )
A.k<0
B.k>2
C.k<2
D.k<﹣2
【分析】先根据不等式的基本性质及此不等式的解集判断出k﹣4的符号,再求出k的取值范围即可.
【解答】解:∵不等式(k﹣2)x>k﹣2的解集是x<1,,
∴k﹣2<0,
∴k<2,
故选:C.
9.(3分)足球比赛的得分规则如下:胜一场得3分,平一场得1分,负一场得0分.某足球队一共进行了14场比赛,其中负了5场,共得19分.设该球队胜了x场,平了y场,依题意可列方程组( )
A.
B.
C.
D.
【分析】设该球队胜了x场,平了y场,根据进行14场比赛,其中负了5场,共得19分,列方程组.
【解答】解:设该球队胜了x场,平了y场,
由题意得.
故选:A.
10.(3分)有下列说法:
(1)外角和为360°的多边形一定是三角形;
(2)有两条边分别相等的两个三角形是全等三角形;
(3)角的平分线上的点到角的两边的距离相等;
(4)如果∠A=∠B+∠C,那么△ABC是直角三角形.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
【分析】根据多边形的外角和定理,全等三角形的判定定理,邻补角定义,角平分线性质,直角三角形的定义分别判断即可.
【解答】解:∵多边形的外角和都等于360°,∴说法(1)错误;
∵全等三角形的判定定理是SAS,ASA,AAS,SSS,有两条边分别相等的两个三角形不符合全等的条件,即两个三角形不全等,∴说法(2)错误;
∵角的平分线上的点到角的两边的距离相等,∴说法(3)正确;
∵三角形的内角和为180°,即∠A+∠B+∠C=180°,∵∠A=∠B+∠C,∴2∠A=180°,∠A=90°,∴△ABC为直角三角形,∴说法(4)正确;
故选:B.
二、填空题(每小题3分,共计30分)
11.(3分)已知4x﹣2y=3,用含x的代数式表示y,则y= 2x﹣1.5 .
【分析】把x看作已知数求出y即可.
【解答】解:4x﹣2y=3,
2y=4x﹣3,
解得:y=2x﹣1.5,
故答案为:2x﹣1.5.
12.(3分)x的3倍与7的和大于9,用不等式可表示为
3x+7>9 .
【分析】关系式为:x的3倍+7>9,把相关数值代入即可.
【解答】解:根据题意,可列不等式为:3x+7>9,
故答案为:3x+7>9.
13.(3分)甲、乙两台机床生产一种零件,10天中两台机床每天生产次品的平均数都是2,方差是S甲2=0.76,S乙2=1.65,两台机床出次品的波动较小的是
甲 机床.(填“甲”或“乙”)
【分析】根据方差的定义,方差越小数据越稳定,即可得出答案.
【解答】解:∵S甲2=0.76,S乙2=1.65,
∴S甲2<S乙2,
∴两台机床出次品的波动较小的是甲机床,
故答案为:甲.
14.(3分)若是关于x、y的方程kx﹣2y=2的一个解,则k= 6 .
【分析】把方程的解代入方程,得到关于k的方程,解方程即可.
【解答】解:把方程的解代入方程得:
2k﹣10=2,
∴k=6,
故答案为:6.
15.(3分)某公司招聘员工,公司对应聘人员进行三项测试:语言、设计和综合知识.公司将把三项测试得分按2:3:4的比确定每人的最后成绩,已知小王三项测试得分依次为90分、81分和72分,则他的最后成绩为
79 分.
【分析】根据加权平均数的计算方法进行计算即可.
【解答】解:90×+81×+72×=79(分),
故答案为:79.
16.(3分)一个等腰三角形的两边长分别为3和7,这个三角形的周长是 17 .
【分析】求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为3和7,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)若3为腰长,7为底边长,
由于3+3<7,则三角形不存在;
(2)若7为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为7+7+3=17.
故答案为:17.
17.(3分)如图,∠ABD=15°,∠ACD=30°,∠A=45°,则∠BDC的度数为
90 °.
【分析】延长BD交AC于点E,两次利用三角形外角的性质可得∠BDC=∠A+∠ABD+∠ACD,进而可求解.
【解答】解:延长BD交AC于点E,
∵∠CEB=∠A+∠ABD,∠BDC=∠CEB+∠ACD,
∴∠BDC=∠A+∠ABD+∠ACD,
∵∠ABD=15°,∠ACD=30°,∠A=45°,
∴∠BDC=45°+30°+15°=90°,
故答案为90.
18.(3分)某次知识竞赛共有20题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少答对 13 道.
【分析】根据小明得分要超过90分,就可以得到不等关系:小明的得分≤90分,设应答对x道,则根据不等关系就可以列出不等式求解.
【解答】解:设应答对x道,则10x﹣5(20﹣x)>90
解得x>12
∴x=13
19.(3分)已知AH为△ABC的高,若∠B=40°,∠ACH=65°,则∠BAC的度数为
25或75 °.
【分析】当∠C是钝角三角形时,由三角形的外角性质即可求出∠BAC的度数,当∠C是锐角时,由三角形内角和定理即可求出∠BAC的度数.
【解答】解:如图,当△ABC是钝角三角形时,
∵∠B=40°,∠ACH=65°,∠ACH=∠BAC+∠B,
∴∠BAC=∠ACH﹣∠B=65°﹣40°=25°;
如图,当△ABC是锐角三角形时,
∵∠B=40°,∠ACH=65°,∠BAC+∠ACH+∠B=180°,
∴∠BAC=180°﹣∠ACH﹣∠B=180°﹣65°﹣40°=75°.
故答案为:25或75.
20.(3分)如图,在△ABC中,点D为AC边的中点,过点C作CF∥AB,过点D作直线EF交AB于点E,交直线CF于点F,若BE=9,CF=6,△ABC的面积为50,则△CDF的面积为
10 .
【分析】根据ASA即可判定△AED≌△CFD,得出AE=CF,S△ADE=S△CDF,根据等高的三角形面积比等于高所在的边的比得出S△AED=S△ABD,S△ABD=S△CBD=S△ABC,据此即可得解.
【解答】解:∵点D为AC边的中点,
∴AD=CD,
∵CF∥AB,
∴∠A=∠FCD,
在△AED和△CFD中,
,
∴△AED≌△CFD(ASA),
∴AE=CF,S△ADE=S△CDF,
∵BE=9,CF=6,
∴AE=6,
∴AB=AE+BE=15,
∴AE=AB,
∴S△AED=S△ABD,
∵D为AC边的中点,△ABC的面积为50,
∴S△ABD=S△CBD=S△ABC=25,
∴S△ADE=S△CDF=×25=10,
故答案为:10.
三、解答题(21-25每题各8分,26,27题各10分)
21.(8分)解下列方程组及不等式组:
(1);
(2).
【分析】(1)利用代入消元法求解即可;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:(1),
由①得,x=y+3
③,
把③代入②得,3(y+3)﹣8y=14,解得y=﹣1,
把y=﹣1代入③得x=2,
∴这个方程组的解是;
(2),
解不等式①得x<1,
解不等式②得x<4,
∴不等式组的解集为x<1.
22.(8分)如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC的边BC上的高AD;
(2)画出△ABC的边AC上的中线BE;
(3)直接写出△ABE的面积为
3 .
【分析】(1)根据三角形的高的定义作出图形即可.
(2)根据三角形的中线的定义作出图形即可.
(3)利用三角形的中线的性质求出△BCE的面积即可解决问题.
【解答】解:(1)如图,线段AD即为所求.
(2)如图,线段BE即为所求,
(3)∵AE=EB,
∴△ABE的面积=△BEC的面积=×3×2=3.
故答案为:3.
23.(8分)为了调查学生每天零花钱情况,对我校七年级某班50名同学每天零花钱情况进行了统计,并绘制成下面的统计图:
(1)这50名同学零花钱的众数为
20 ;中位数为
20 ;
(2)求这50名同学零花钱的平均数;
(3)该校共有学生3000人,请你根据该班的零花钱情况,估计这所中学学生每天的零花钱总数是多少元?
【分析】(1)根据中位数和众数的定义解答即可;
(2)根据平均数的公式计算即可;
(3)用总数乘以这50名同学零花钱的平均数即可得到这个中学学生的零花钱总数.
【解答】解:(1)这50名同学零花钱的众数为20;中位数为20;
故答案为:20;20;
(2)(元).
答:这50名同学零花钱的平均数是18元.
(3)由样本估计总体得:18×3000=54000(元).
答:估计这所中学学生每天的零花钱总数是54000元.
24.(8分)如图,在△ABC中,AB=AC,BE⊥AC于点E,CF⊥AB于点F,且BE与CF相交于点O.
(1)求证:BF=CE;
(2)不添加辅助线,直接写出图中所有的全等三角形.
【分析】(1)由△AEB≌△AFC(AAS)的对应边相等得到:AE=AF.结合已知条件和图形中相关线段间的数量关系证得结论;
(2)根据全等三角形的判定定理写出答案.
【解答】(1)证明:∵BE⊥AC于点E,CF⊥AB于点F,
∴∠CEB=∠BFC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
即∠FBC=∠ECB,
在△BCF和△CBE中,
,
∴△BCF≌△CBE(AAS),
∴BF=CE;
(2)解:由(1)知△BCF≌△CBE(AAS),
在△AEB和△AFC中,
,
∴△AEB≌△AFC(AAS),
在△BFO和△CEO中,
,
∴△BFO≌△CEO(AAS).
25.(8分)学校为丰富学生的业余生活,为学生购买排球和篮球.若买10个排球和8个篮球需1600元;若买15个排球和20个篮球需3200元.
(1)每个排球和篮球的售价分别多少元?
(2)若学校打算购买排球和篮球共50个,购买的费用不超过4680元,则至少购买排球多少个?
【分析】(1)设每个排球的售价为x元,每个篮球的售价为y元,根据“若买10个排球和8个篮球需1600元;若买15个排球和20个篮球需3200元”,即可得出关于x,y的二元一次方程组,解之即可得出每个排球和篮球的售价;
(2)设购买排球m个,则购买篮球(50﹣m)个,利用总价=单价×数量,结合购买的费用不超过4680元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出至少购买排球16个.
【解答】解:(1)设每个排球的售价为x元,每个篮球的售价为y元,
依题意得:,
解得:.
答:每个排球的售价为80元,每个篮球的售价为100元.
(2)设购买排球m个,则购买篮球(50﹣m)个,
依题意得:80m+100(50﹣m)≤4680,
解得:m≥16.
答:至少购买排球16个.
26.(10分)在△ABC中,AB=AC.
(1)如图1,求证:∠B=∠C;
(2)如图2,D为AB上一点,连接CD,E为CD中点,过点E作EF⊥CD于点E,连接FC、FD,求证:FC=FD;
(3)如图3,在(2)的条件下,过点F作FH⊥AC于点H,连接AF,若AF∥BC,FH=4,CH=20,BD=10,求△ADF的面积.
【分析】(1)过点A作AM⊥BC于点M,证明Rt△AMB≌Rt△AMC(HL),由全等三角形的性质得出∠B=∠C;
(2)证明△FED≌△FEC(SAS),由全等三角形的性质得出FD=FC;
(3)过点F作FG⊥BA延长线于点G,证明Rt△AGF≌Rt△AHF(HL),得出AG=AH,Rt△GDF≌Rt△HCF(HL),得出GD=HC,求出AD的长,由三角形面积公式可得出答案.
【解答】(1)证明:过点A作AM⊥BC于点M,
∵AM⊥BC,
∴∠AMB=∠AMC=90°,
在Rt△AMB和Rt△AMC中,
,
∴Rt△AMB≌Rt△AMC(HL),
∴∠B=∠C;
(2)证明:∵EF⊥CD,
∴∠FED=∠FEC=90°,
∵E为CD中点,
∴DE=CE,
在△FED和△FEC中,
,
∴△FED≌△FEC(SAS),
∴FD=FC;
(3)解:过点F作FG⊥BA延长线于点G,
∵FH⊥AC,FG⊥DG,
∴∠FHA=∠FHC=∠G=90°,
∵AF//BC,
∴∠GAF=∠B,∠HAF=∠ACB,
∵∠B=∠ACB,
∴∠GAF=∠HAF,
∵FG⊥BA,FH⊥AC,
∴FG=FH,
在Rt△AGF和Rt△AHF中,
,
∴Rt△AGF≌Rt△AHF(HL),
∴AG=AH,
在Rt△GDF和Rt△HCF中,
,
∴Rt△GDF≌Rt△HCF(HL),
∴GD=HC,
∴AD+AG=AC﹣AH,
∴AB﹣BD+AG=AC﹣AH,
∵AB=AC,AG=AH,
∴2AH=BD,
∵BD=10,
∴AH=AG=5,
∵CH=20,
∴AB=AC=AH+CH=5+20=25,
∵BD=10,
∴AD=AB﹣BD=25﹣10=15,
∵FG=FH=4,
∴△ADF的面积=.
27.(10分)如图,在平面直角坐标系中,点O为坐标原点,点A(0,a)在y轴正半轴上,点B(b,0)在x轴正半轴上,且a,b是方程组的解.
(1)直接写出点A的坐标为
(0,6) ,点B的坐标为
(4,0) ;
(2)动点P从点B出发,以每秒1个单位长度的速度沿射线BO方向运动,连接AP,设P点的运动时间为t秒,△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)在(2)的条件下,当点P在x轴负半轴上时,且S=6,在y轴负半轴上有一点C,过点B作x轴垂线,与射线PC交于点D,若∠CPO+2∠APO=180°,PD=,连接AD,交OB于点E,求点E的坐标.
【分析】(1)解方程组可求a,b的值,即可求解;
(2)分两种情况讨论,当点P在线段BO上时,当点P在线段BO延长线上时,利用三角形的面积公式可求解;
(3)由三角形面积求出BP=6,过点A作AF⊥DP,交DP的延长线于点F,证明△AFP≌△AOP(AAS),由全等三角形的性质可得出AF=AO=6,过点A作AG⊥DB,交DB的延长线于点G,由四边形APDB的面积可求出BD的长,求出BE的长,则可得出答案.
【解答】解:(1)∵,
∴,
∴A(0,6),B(4,0),
故答案为(0,6),(4,0);
(2)当点P在线段BO上时,OP=4﹣t,
∴S=OP?OA=(4﹣t)×6=12﹣3t(0≤t<4);
当点P在线段BO延长线上时,OP=t﹣4,
∴S=OP?OA=(t﹣4)×6=3t﹣12(t>4).
(3)由(2)得:3t﹣12=6,
解得t=6,
∴BP=6,
∵A(0,6),B(4,0),
∴OA=6,OB=4,
过点A作AF⊥DP,交DP的延长线于点F,
∵∠CPO+2∠APO=180°,∠CPO+∠APO+∠APF=180°,
∴∠APF=∠APO,
在△AFP和△AOP中,
,
∴△AFP≌△AOP(AAS),
∴AF=AO=6,
过点A作AG⊥DB,交DB的延长线于点G,
∵S四边形APDB=S△APD+S△ADB,S四边形APDB=S△APB+S△DPB,
∴S△APD+S△ADB=S△APB+S△DPB,
∴×PB×BD,
∴PD×AF+BD×AG=PB×OA+PB×BD,
∴×6+BD×4=6×6+6×BD,
∴BD=,
∴DG=BG+BD=6+,
∵S△ADG=S△DBE+S梯形AGBE,
∴×(BE+AG)×BG,
∴DG×AG=BD×BE+(BE+AG)×BG,
∴×BE+(BE+4)×6,
∴BE=,
∴OE=OB﹣BE=4﹣,
∴.
一、选择题(每小题3分,共计30分)
1.(3分)下列方程中,是二元一次方程的是( )
A.2x+=8
B.﹣x2+2y=7
C.﹣x+2=9
D.7x﹣2y=13
2.(3分)如果x>y,则下列变形中正确的是( )
A.﹣xy
B.y
C.3x>5y
D.x﹣3>y﹣3
3.(3分)下列长度的三条线段中,能组成三角形的是( )
A.2cm,5cm,7cm
B.0.1cm,0.1cm,0.1cm
C.8cm,8cm,17cm
D.7cm,40cm,8cm
4.(3分)把不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
5.(3分)下列四个图形中,线段BE是△ABC的高的图形是( )
A.
B.
C.
D.
6.(3分)一个凸n边形,其每个内角都是140°,则n的值为( )
A.6
B.7
C.8
D.9
7.(3分)如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠使点A落在BC边上的点A′处,折痕为CD,则∠A′DC=( )
A.10°
B.30°
C.65°
D.85°
8.(3分)若不等式(k﹣2)x>k﹣2的解集是x<1,则k满足( )
A.k<0
B.k>2
C.k<2
D.k<﹣2
9.(3分)足球比赛的得分规则如下:胜一场得3分,平一场得1分,负一场得0分.某足球队一共进行了14场比赛,其中负了5场,共得19分.设该球队胜了x场,平了y场,依题意可列方程组( )
A.
B.
C.
D.
10.(3分)有下列说法:
(1)外角和为360°的多边形一定是三角形;
(2)有两条边分别相等的两个三角形是全等三角形;
(3)角的平分线上的点到角的两边的距离相等;
(4)如果∠A=∠B+∠C,那么△ABC是直角三角形.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共计30分)
11.(3分)已知4x﹣2y=3,用含x的代数式表示y,则y=
.
12.(3分)x的3倍与7的和大于9,用不等式可表示为
.
13.(3分)甲、乙两台机床生产一种零件,10天中两台机床每天生产次品的平均数都是2,方差是S甲2=0.76,S乙2=1.65,两台机床出次品的波动较小的是
机床.(填“甲”或“乙”)
14.(3分)若是关于x、y的方程kx﹣2y=2的一个解,则k=
.
15.(3分)某公司招聘员工,公司对应聘人员进行三项测试:语言、设计和综合知识.公司将把三项测试得分按2:3:4的比确定每人的最后成绩,已知小王三项测试得分依次为90分、81分和72分,则他的最后成绩为
分.
16.(3分)一个等腰三角形的两边长分别为3和7,这个三角形的周长是
.
17.(3分)如图,∠ABD=15°,∠ACD=30°,∠A=45°,则∠BDC的度数为
°.
18.(3分)某次知识竞赛共有20题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少答对
道.
19.(3分)已知AH为△ABC的高,若∠B=40°,∠ACH=65°,则∠BAC的度数为
°.
20.(3分)如图,在△ABC中,点D为AC边的中点,过点C作CF∥AB,过点D作直线EF交AB于点E,交直线CF于点F,若BE=9,CF=6,△ABC的面积为50,则△CDF的面积为
.
三、解答题(21-25每题各8分,26,27题各10分)
21.(8分)解下列方程组及不等式组:
(1);
(2).
22.(8分)如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC的边BC上的高AD;
(2)画出△ABC的边AC上的中线BE;
(3)直接写出△ABE的面积为
.
23.(8分)为了调查学生每天零花钱情况,对我校七年级某班50名同学每天零花钱情况进行了统计,并绘制成下面的统计图:
(1)这50名同学零花钱的众数为
;中位数为
;
(2)求这50名同学零花钱的平均数;
(3)该校共有学生3000人,请你根据该班的零花钱情况,估计这所中学学生每天的零花钱总数是多少元?
24.(8分)如图,在△ABC中,AB=AC,BE⊥AC于点E,CF⊥AB于点F,且BE与CF相交于点O.
(1)求证:BF=CE;
(2)不添加辅助线,直接写出图中所有的全等三角形.
25.(8分)学校为丰富学生的业余生活,为学生购买排球和篮球.若买10个排球和8个篮球需1600元;若买15个排球和20个篮球需3200元.
(1)每个排球和篮球的售价分别多少元?
(2)若学校打算购买排球和篮球共50个,购买的费用不超过4680元,则至少购买排球多少个?
26.(10分)在△ABC中,AB=AC.
(1)如图1,求证:∠B=∠C;
(2)如图2,D为AB上一点,连接CD,E为CD中点,过点E作EF⊥CD于点E,连接FC、FD,求证:FC=FD;
(3)如图3,在(2)的条件下,过点F作FH⊥AC于点H,连接AF,若AF∥BC,FH=4,CH=20,BD=10,求△ADF的面积.
27.(10分)如图,在平面直角坐标系中,点O为坐标原点,点A(0,a)在y轴正半轴上,点B(b,0)在x轴正半轴上,且a,b是方程组的解.
(1)直接写出点A的坐标为
,点B的坐标为
;
(2)动点P从点B出发,以每秒1个单位长度的速度沿射线BO方向运动,连接AP,设P点的运动时间为t秒,△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)在(2)的条件下,当点P在x轴负半轴上时,且S=6,在y轴负半轴上有一点C,过点B作x轴垂线,与射线PC交于点D,若∠CPO+2∠APO=180°,PD=,连接AD,交OB于点E,求点E的坐标.
2020-2021学年黑龙江省哈尔滨市松北区七年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.(3分)下列方程中,是二元一次方程的是( )
A.2x+=8
B.﹣x2+2y=7
C.﹣x+2=9
D.7x﹣2y=13
【分析】根据二元一次方程的定义即可求出答案.
【解答】解:A、该方程不是整式方程,故不符合题意.
B、该方程中含有两个未知数,但未知数的最高次数是2,不是二元一次方程,故不符合题意.
C、该方程是一元一次方程,故不符合题意.
D、该方程属于二元一次方程,故不符合题意.
故选:D.
2.(3分)如果x>y,则下列变形中正确的是( )
A.﹣xy
B.y
C.3x>5y
D.x﹣3>y﹣3
【分析】根据不等式的性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变.不等式两边乘(或除以)同一个负数,不等号的方向改变.
【解答】解:A、两边都乘以﹣,故A错误;
B、两边都乘以,故B错误;
C、左边乘3,右边乘5,故C错误;
D、两边都减3,故D正确;
故选:D.
3.(3分)下列长度的三条线段中,能组成三角形的是( )
A.2cm,5cm,7cm
B.0.1cm,0.1cm,0.1cm
C.8cm,8cm,17cm
D.7cm,40cm,8cm
【分析】看哪个选项中两条较小的边的和大于最大的边即可.
【解答】解:A、2+5=7,不能构成三角形;
B、0.1+0.1>0.1,能构成三角形;
C、8+8<17,不能构成三角形;
D、7+8<40,不能构成三角形.
故选:B.
4.(3分)把不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
【分析】分别把两条不等式解出来,然后判断哪个选项表示的正确.
【解答】解:由(1)得:x≥﹣1,
由(2)得:x<2,
所以﹣1≤x<2.
故选:C.
5.(3分)下列四个图形中,线段BE是△ABC的高的图形是( )
A.
B.
C.
D.
【分析】根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解答】解:线段BE是△ABC的高的图是选项A.
故选:A.
6.(3分)一个凸n边形,其每个内角都是140°,则n的值为( )
A.6
B.7
C.8
D.9
【分析】根据多边形每个内角与其相邻的内角互补,则正n边形的每个外角的度数=180°﹣140°=40°,然后根据多边形的外角和为360°即可得到n的值.
【解答】解:∵正n边形的每个内角都是140°,
∴正n边形的每个外角的度数=180°﹣140°=40°,
∴n==9.
故选:D.
7.(3分)如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠使点A落在BC边上的点A′处,折痕为CD,则∠A′DC=( )
A.10°
B.30°
C.65°
D.85°
【分析】根据翻折变换的性质可得∠A′DC=∠ADC,CD是角平分线,然后根据三角形的内角和列式计算即可得解.
【解答】解:∵折叠后点A落在边CB上A′处,∠ACB=90°
∴折痕CD是角平分线,
∴∠A′CD=∠ACD=45°
又∵∠A=50°,
∴∠A′DC=∠ADC=180°﹣∠A﹣∠ACD=180°﹣50°﹣45°=85°.
故选:D.
8.(3分)若不等式(k﹣2)x>k﹣2的解集是x<1,则k满足( )
A.k<0
B.k>2
C.k<2
D.k<﹣2
【分析】先根据不等式的基本性质及此不等式的解集判断出k﹣4的符号,再求出k的取值范围即可.
【解答】解:∵不等式(k﹣2)x>k﹣2的解集是x<1,,
∴k﹣2<0,
∴k<2,
故选:C.
9.(3分)足球比赛的得分规则如下:胜一场得3分,平一场得1分,负一场得0分.某足球队一共进行了14场比赛,其中负了5场,共得19分.设该球队胜了x场,平了y场,依题意可列方程组( )
A.
B.
C.
D.
【分析】设该球队胜了x场,平了y场,根据进行14场比赛,其中负了5场,共得19分,列方程组.
【解答】解:设该球队胜了x场,平了y场,
由题意得.
故选:A.
10.(3分)有下列说法:
(1)外角和为360°的多边形一定是三角形;
(2)有两条边分别相等的两个三角形是全等三角形;
(3)角的平分线上的点到角的两边的距离相等;
(4)如果∠A=∠B+∠C,那么△ABC是直角三角形.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
【分析】根据多边形的外角和定理,全等三角形的判定定理,邻补角定义,角平分线性质,直角三角形的定义分别判断即可.
【解答】解:∵多边形的外角和都等于360°,∴说法(1)错误;
∵全等三角形的判定定理是SAS,ASA,AAS,SSS,有两条边分别相等的两个三角形不符合全等的条件,即两个三角形不全等,∴说法(2)错误;
∵角的平分线上的点到角的两边的距离相等,∴说法(3)正确;
∵三角形的内角和为180°,即∠A+∠B+∠C=180°,∵∠A=∠B+∠C,∴2∠A=180°,∠A=90°,∴△ABC为直角三角形,∴说法(4)正确;
故选:B.
二、填空题(每小题3分,共计30分)
11.(3分)已知4x﹣2y=3,用含x的代数式表示y,则y= 2x﹣1.5 .
【分析】把x看作已知数求出y即可.
【解答】解:4x﹣2y=3,
2y=4x﹣3,
解得:y=2x﹣1.5,
故答案为:2x﹣1.5.
12.(3分)x的3倍与7的和大于9,用不等式可表示为
3x+7>9 .
【分析】关系式为:x的3倍+7>9,把相关数值代入即可.
【解答】解:根据题意,可列不等式为:3x+7>9,
故答案为:3x+7>9.
13.(3分)甲、乙两台机床生产一种零件,10天中两台机床每天生产次品的平均数都是2,方差是S甲2=0.76,S乙2=1.65,两台机床出次品的波动较小的是
甲 机床.(填“甲”或“乙”)
【分析】根据方差的定义,方差越小数据越稳定,即可得出答案.
【解答】解:∵S甲2=0.76,S乙2=1.65,
∴S甲2<S乙2,
∴两台机床出次品的波动较小的是甲机床,
故答案为:甲.
14.(3分)若是关于x、y的方程kx﹣2y=2的一个解,则k= 6 .
【分析】把方程的解代入方程,得到关于k的方程,解方程即可.
【解答】解:把方程的解代入方程得:
2k﹣10=2,
∴k=6,
故答案为:6.
15.(3分)某公司招聘员工,公司对应聘人员进行三项测试:语言、设计和综合知识.公司将把三项测试得分按2:3:4的比确定每人的最后成绩,已知小王三项测试得分依次为90分、81分和72分,则他的最后成绩为
79 分.
【分析】根据加权平均数的计算方法进行计算即可.
【解答】解:90×+81×+72×=79(分),
故答案为:79.
16.(3分)一个等腰三角形的两边长分别为3和7,这个三角形的周长是 17 .
【分析】求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为3和7,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:(1)若3为腰长,7为底边长,
由于3+3<7,则三角形不存在;
(2)若7为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为7+7+3=17.
故答案为:17.
17.(3分)如图,∠ABD=15°,∠ACD=30°,∠A=45°,则∠BDC的度数为
90 °.
【分析】延长BD交AC于点E,两次利用三角形外角的性质可得∠BDC=∠A+∠ABD+∠ACD,进而可求解.
【解答】解:延长BD交AC于点E,
∵∠CEB=∠A+∠ABD,∠BDC=∠CEB+∠ACD,
∴∠BDC=∠A+∠ABD+∠ACD,
∵∠ABD=15°,∠ACD=30°,∠A=45°,
∴∠BDC=45°+30°+15°=90°,
故答案为90.
18.(3分)某次知识竞赛共有20题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少答对 13 道.
【分析】根据小明得分要超过90分,就可以得到不等关系:小明的得分≤90分,设应答对x道,则根据不等关系就可以列出不等式求解.
【解答】解:设应答对x道,则10x﹣5(20﹣x)>90
解得x>12
∴x=13
19.(3分)已知AH为△ABC的高,若∠B=40°,∠ACH=65°,则∠BAC的度数为
25或75 °.
【分析】当∠C是钝角三角形时,由三角形的外角性质即可求出∠BAC的度数,当∠C是锐角时,由三角形内角和定理即可求出∠BAC的度数.
【解答】解:如图,当△ABC是钝角三角形时,
∵∠B=40°,∠ACH=65°,∠ACH=∠BAC+∠B,
∴∠BAC=∠ACH﹣∠B=65°﹣40°=25°;
如图,当△ABC是锐角三角形时,
∵∠B=40°,∠ACH=65°,∠BAC+∠ACH+∠B=180°,
∴∠BAC=180°﹣∠ACH﹣∠B=180°﹣65°﹣40°=75°.
故答案为:25或75.
20.(3分)如图,在△ABC中,点D为AC边的中点,过点C作CF∥AB,过点D作直线EF交AB于点E,交直线CF于点F,若BE=9,CF=6,△ABC的面积为50,则△CDF的面积为
10 .
【分析】根据ASA即可判定△AED≌△CFD,得出AE=CF,S△ADE=S△CDF,根据等高的三角形面积比等于高所在的边的比得出S△AED=S△ABD,S△ABD=S△CBD=S△ABC,据此即可得解.
【解答】解:∵点D为AC边的中点,
∴AD=CD,
∵CF∥AB,
∴∠A=∠FCD,
在△AED和△CFD中,
,
∴△AED≌△CFD(ASA),
∴AE=CF,S△ADE=S△CDF,
∵BE=9,CF=6,
∴AE=6,
∴AB=AE+BE=15,
∴AE=AB,
∴S△AED=S△ABD,
∵D为AC边的中点,△ABC的面积为50,
∴S△ABD=S△CBD=S△ABC=25,
∴S△ADE=S△CDF=×25=10,
故答案为:10.
三、解答题(21-25每题各8分,26,27题各10分)
21.(8分)解下列方程组及不等式组:
(1);
(2).
【分析】(1)利用代入消元法求解即可;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:(1),
由①得,x=y+3
③,
把③代入②得,3(y+3)﹣8y=14,解得y=﹣1,
把y=﹣1代入③得x=2,
∴这个方程组的解是;
(2),
解不等式①得x<1,
解不等式②得x<4,
∴不等式组的解集为x<1.
22.(8分)如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC的边BC上的高AD;
(2)画出△ABC的边AC上的中线BE;
(3)直接写出△ABE的面积为
3 .
【分析】(1)根据三角形的高的定义作出图形即可.
(2)根据三角形的中线的定义作出图形即可.
(3)利用三角形的中线的性质求出△BCE的面积即可解决问题.
【解答】解:(1)如图,线段AD即为所求.
(2)如图,线段BE即为所求,
(3)∵AE=EB,
∴△ABE的面积=△BEC的面积=×3×2=3.
故答案为:3.
23.(8分)为了调查学生每天零花钱情况,对我校七年级某班50名同学每天零花钱情况进行了统计,并绘制成下面的统计图:
(1)这50名同学零花钱的众数为
20 ;中位数为
20 ;
(2)求这50名同学零花钱的平均数;
(3)该校共有学生3000人,请你根据该班的零花钱情况,估计这所中学学生每天的零花钱总数是多少元?
【分析】(1)根据中位数和众数的定义解答即可;
(2)根据平均数的公式计算即可;
(3)用总数乘以这50名同学零花钱的平均数即可得到这个中学学生的零花钱总数.
【解答】解:(1)这50名同学零花钱的众数为20;中位数为20;
故答案为:20;20;
(2)(元).
答:这50名同学零花钱的平均数是18元.
(3)由样本估计总体得:18×3000=54000(元).
答:估计这所中学学生每天的零花钱总数是54000元.
24.(8分)如图,在△ABC中,AB=AC,BE⊥AC于点E,CF⊥AB于点F,且BE与CF相交于点O.
(1)求证:BF=CE;
(2)不添加辅助线,直接写出图中所有的全等三角形.
【分析】(1)由△AEB≌△AFC(AAS)的对应边相等得到:AE=AF.结合已知条件和图形中相关线段间的数量关系证得结论;
(2)根据全等三角形的判定定理写出答案.
【解答】(1)证明:∵BE⊥AC于点E,CF⊥AB于点F,
∴∠CEB=∠BFC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
即∠FBC=∠ECB,
在△BCF和△CBE中,
,
∴△BCF≌△CBE(AAS),
∴BF=CE;
(2)解:由(1)知△BCF≌△CBE(AAS),
在△AEB和△AFC中,
,
∴△AEB≌△AFC(AAS),
在△BFO和△CEO中,
,
∴△BFO≌△CEO(AAS).
25.(8分)学校为丰富学生的业余生活,为学生购买排球和篮球.若买10个排球和8个篮球需1600元;若买15个排球和20个篮球需3200元.
(1)每个排球和篮球的售价分别多少元?
(2)若学校打算购买排球和篮球共50个,购买的费用不超过4680元,则至少购买排球多少个?
【分析】(1)设每个排球的售价为x元,每个篮球的售价为y元,根据“若买10个排球和8个篮球需1600元;若买15个排球和20个篮球需3200元”,即可得出关于x,y的二元一次方程组,解之即可得出每个排球和篮球的售价;
(2)设购买排球m个,则购买篮球(50﹣m)个,利用总价=单价×数量,结合购买的费用不超过4680元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出至少购买排球16个.
【解答】解:(1)设每个排球的售价为x元,每个篮球的售价为y元,
依题意得:,
解得:.
答:每个排球的售价为80元,每个篮球的售价为100元.
(2)设购买排球m个,则购买篮球(50﹣m)个,
依题意得:80m+100(50﹣m)≤4680,
解得:m≥16.
答:至少购买排球16个.
26.(10分)在△ABC中,AB=AC.
(1)如图1,求证:∠B=∠C;
(2)如图2,D为AB上一点,连接CD,E为CD中点,过点E作EF⊥CD于点E,连接FC、FD,求证:FC=FD;
(3)如图3,在(2)的条件下,过点F作FH⊥AC于点H,连接AF,若AF∥BC,FH=4,CH=20,BD=10,求△ADF的面积.
【分析】(1)过点A作AM⊥BC于点M,证明Rt△AMB≌Rt△AMC(HL),由全等三角形的性质得出∠B=∠C;
(2)证明△FED≌△FEC(SAS),由全等三角形的性质得出FD=FC;
(3)过点F作FG⊥BA延长线于点G,证明Rt△AGF≌Rt△AHF(HL),得出AG=AH,Rt△GDF≌Rt△HCF(HL),得出GD=HC,求出AD的长,由三角形面积公式可得出答案.
【解答】(1)证明:过点A作AM⊥BC于点M,
∵AM⊥BC,
∴∠AMB=∠AMC=90°,
在Rt△AMB和Rt△AMC中,
,
∴Rt△AMB≌Rt△AMC(HL),
∴∠B=∠C;
(2)证明:∵EF⊥CD,
∴∠FED=∠FEC=90°,
∵E为CD中点,
∴DE=CE,
在△FED和△FEC中,
,
∴△FED≌△FEC(SAS),
∴FD=FC;
(3)解:过点F作FG⊥BA延长线于点G,
∵FH⊥AC,FG⊥DG,
∴∠FHA=∠FHC=∠G=90°,
∵AF//BC,
∴∠GAF=∠B,∠HAF=∠ACB,
∵∠B=∠ACB,
∴∠GAF=∠HAF,
∵FG⊥BA,FH⊥AC,
∴FG=FH,
在Rt△AGF和Rt△AHF中,
,
∴Rt△AGF≌Rt△AHF(HL),
∴AG=AH,
在Rt△GDF和Rt△HCF中,
,
∴Rt△GDF≌Rt△HCF(HL),
∴GD=HC,
∴AD+AG=AC﹣AH,
∴AB﹣BD+AG=AC﹣AH,
∵AB=AC,AG=AH,
∴2AH=BD,
∵BD=10,
∴AH=AG=5,
∵CH=20,
∴AB=AC=AH+CH=5+20=25,
∵BD=10,
∴AD=AB﹣BD=25﹣10=15,
∵FG=FH=4,
∴△ADF的面积=.
27.(10分)如图,在平面直角坐标系中,点O为坐标原点,点A(0,a)在y轴正半轴上,点B(b,0)在x轴正半轴上,且a,b是方程组的解.
(1)直接写出点A的坐标为
(0,6) ,点B的坐标为
(4,0) ;
(2)动点P从点B出发,以每秒1个单位长度的速度沿射线BO方向运动,连接AP,设P点的运动时间为t秒,△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)在(2)的条件下,当点P在x轴负半轴上时,且S=6,在y轴负半轴上有一点C,过点B作x轴垂线,与射线PC交于点D,若∠CPO+2∠APO=180°,PD=,连接AD,交OB于点E,求点E的坐标.
【分析】(1)解方程组可求a,b的值,即可求解;
(2)分两种情况讨论,当点P在线段BO上时,当点P在线段BO延长线上时,利用三角形的面积公式可求解;
(3)由三角形面积求出BP=6,过点A作AF⊥DP,交DP的延长线于点F,证明△AFP≌△AOP(AAS),由全等三角形的性质可得出AF=AO=6,过点A作AG⊥DB,交DB的延长线于点G,由四边形APDB的面积可求出BD的长,求出BE的长,则可得出答案.
【解答】解:(1)∵,
∴,
∴A(0,6),B(4,0),
故答案为(0,6),(4,0);
(2)当点P在线段BO上时,OP=4﹣t,
∴S=OP?OA=(4﹣t)×6=12﹣3t(0≤t<4);
当点P在线段BO延长线上时,OP=t﹣4,
∴S=OP?OA=(t﹣4)×6=3t﹣12(t>4).
(3)由(2)得:3t﹣12=6,
解得t=6,
∴BP=6,
∵A(0,6),B(4,0),
∴OA=6,OB=4,
过点A作AF⊥DP,交DP的延长线于点F,
∵∠CPO+2∠APO=180°,∠CPO+∠APO+∠APF=180°,
∴∠APF=∠APO,
在△AFP和△AOP中,
,
∴△AFP≌△AOP(AAS),
∴AF=AO=6,
过点A作AG⊥DB,交DB的延长线于点G,
∵S四边形APDB=S△APD+S△ADB,S四边形APDB=S△APB+S△DPB,
∴S△APD+S△ADB=S△APB+S△DPB,
∴×PB×BD,
∴PD×AF+BD×AG=PB×OA+PB×BD,
∴×6+BD×4=6×6+6×BD,
∴BD=,
∴DG=BG+BD=6+,
∵S△ADG=S△DBE+S梯形AGBE,
∴×(BE+AG)×BG,
∴DG×AG=BD×BE+(BE+AG)×BG,
∴×BE+(BE+4)×6,
∴BE=,
∴OE=OB﹣BE=4﹣,
∴.
同课章节目录
