2.2.1函数的概念 第1课时 课件(共19张PPT)
文档属性
| 名称 | 2.2.1函数的概念 第1课时 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 14:35:33 | ||
图片预览





文档简介
(共19张PPT)
数学北师大
必修1
2.2.1函数的概念第1课时
初中我们已经学过函数的概念:
在变化过程中,有两个变量x和y
,如果给定一个c值,相应地就确定了一个y值,那么我们称y是工的函数,其中工是自变量,y是因变量.
几百年来,随着数学的发展,对函数概念的理解不断深入,对函数概念的描述越来越清晰.
从集合的观点出发,还可以给出以下的函数定义:
给定两个非空数集A和B,如果按照某个对应关系f,对于集合A中任何一个数x,在集合B中都存在唯一确定的数f(x)与之对应,那么就把对应关系f叫作定义在集合A上的函数,
记作f:A-→B,或y=f(x),x∈A.
此时,x叫作自变量,集合A叫作函数的定义域,
集合{f(x)|x∈A}叫作函数的值域.
习惯上我们称y是x的函数.
【解析】 (1)对于A中的元素3,在f作用下得0,但0?B,即3在B中没有元素与之对应,所以不是函数.
(2)对于A中任意一个非负数都有唯一元素1与之对应,对于A中任意一个负数都有唯一元素0与之对应,所以是函数.
(3)集合A中的负数,在B中没有元素与之对应,故不是函数.
(4)集合A中的元素0在B中没有元素和它对应,故不是函数.
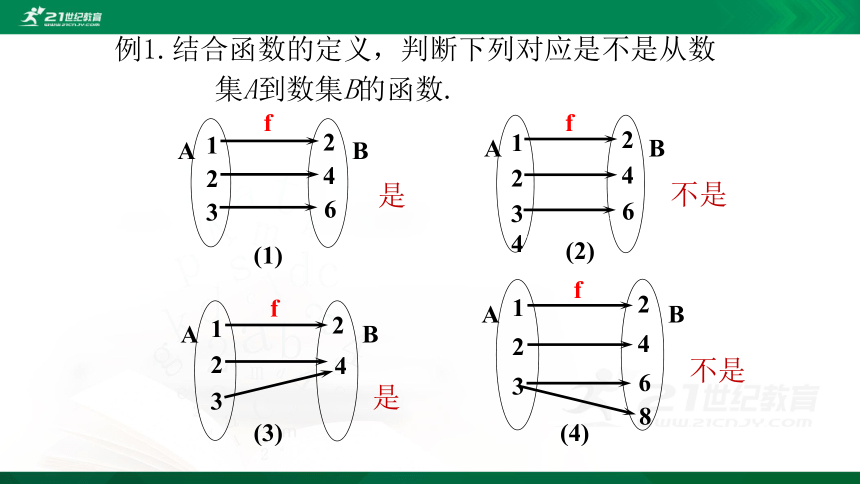
例1.结合函数的定义,判断下列对应是不是从数
集A到数集B的函数.
A
B
f
1
2
2
4
3
6
A
B
f
1
2
2
4
3
6
4
B
A
f
1
2
2
4
3
6
8
A
B
f
1
2
2
4
3
(1)
(4)
(3)
(2)
不是
是
是
不是
A
B
f
1
2
2
4
3
6
8
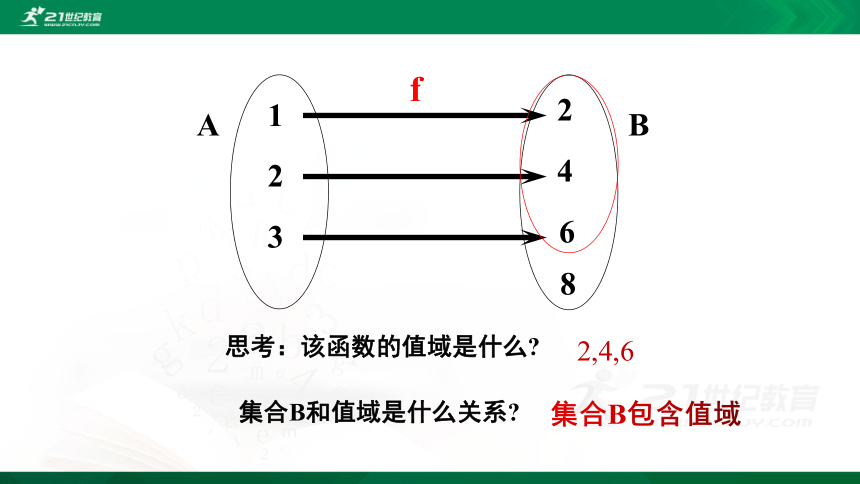
集合B和值域是什么关系?
思考:该函数的值域是什么?
2,4,6
集合B包含值域
有时给出的函数没有明确说明定义域,这时,它的定义域就是自变量的允许取值范围,比如y=
的定义域就是{x|x≠0}.
如果函数涉及实际问题,它的定义域还必须使实际问题有意义.
当x=a时,我们用f(a)表示函数y=f(x)的函数值.
例如,设函数f(x)=3x2+2x-1,
那么,f(5)=3×52+2×5-1=84.84是函数f(x)当x=5时的函数值.
例:已知y=f(2x+1)的定义域为[1,2].
(1)求f(x)的定义域;
(2)求f(2x-1)的定义域.
解:(1)由于y=f(2x+1)的定义域为[1,2],
∴1≤x≤2,∴3≤2x+1≤5,
∴函数f(x)的定义域为[3,5].
(2)由(1)可知,3≤2x-1≤5,∴2≤x≤3,
∴函数f(2x-1)的定义域为[2,3].
①若f(x)是整式,则函数的定义域为R;
②若f(x)是分式,函数的分母不为零;
③偶次根式的被开方数非负;
④零的零次方没有意义;
⑤组合型函数的定义域是各个初等函数定义域的交集.
⑥当函数y=f(x)是用表格给出时,函数的定义域是指表格中实数的集合.
⑦当函数y=f(x)是用图象给出时,函数的定义域是指图象在x轴上投影所覆盖的实数的集合.
如何确定函数的定义域?
课堂小结
1.函数定义:
3.求函数定义域
(1)自然定义域:使函数解析式有意义的自变量的一切值;
(2)限定定义域:受某种条件制约或有附加条件的定义域应用问题、几何问题中的函数定义域,要考虑自变量的实际意义和几何意义.
2.函数的三要素:定义域、值域、对应关系.
作业布置:求下列函数的定义域:
作业布置:求下列函数的定义域:
故函数的定义域为
-2
1
2
定义域为
{5}.
x
{x|x
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大
必修1
2.2.1函数的概念第1课时
初中我们已经学过函数的概念:
在变化过程中,有两个变量x和y
,如果给定一个c值,相应地就确定了一个y值,那么我们称y是工的函数,其中工是自变量,y是因变量.
几百年来,随着数学的发展,对函数概念的理解不断深入,对函数概念的描述越来越清晰.
从集合的观点出发,还可以给出以下的函数定义:
给定两个非空数集A和B,如果按照某个对应关系f,对于集合A中任何一个数x,在集合B中都存在唯一确定的数f(x)与之对应,那么就把对应关系f叫作定义在集合A上的函数,
记作f:A-→B,或y=f(x),x∈A.
此时,x叫作自变量,集合A叫作函数的定义域,
集合{f(x)|x∈A}叫作函数的值域.
习惯上我们称y是x的函数.
【解析】 (1)对于A中的元素3,在f作用下得0,但0?B,即3在B中没有元素与之对应,所以不是函数.
(2)对于A中任意一个非负数都有唯一元素1与之对应,对于A中任意一个负数都有唯一元素0与之对应,所以是函数.
(3)集合A中的负数,在B中没有元素与之对应,故不是函数.
(4)集合A中的元素0在B中没有元素和它对应,故不是函数.
例1.结合函数的定义,判断下列对应是不是从数
集A到数集B的函数.
A
B
f
1
2
2
4
3
6
A
B
f
1
2
2
4
3
6
4
B
A
f
1
2
2
4
3
6
8
A
B
f
1
2
2
4
3
(1)
(4)
(3)
(2)
不是
是
是
不是
A
B
f
1
2
2
4
3
6
8
集合B和值域是什么关系?
思考:该函数的值域是什么?
2,4,6
集合B包含值域
有时给出的函数没有明确说明定义域,这时,它的定义域就是自变量的允许取值范围,比如y=
的定义域就是{x|x≠0}.
如果函数涉及实际问题,它的定义域还必须使实际问题有意义.
当x=a时,我们用f(a)表示函数y=f(x)的函数值.
例如,设函数f(x)=3x2+2x-1,
那么,f(5)=3×52+2×5-1=84.84是函数f(x)当x=5时的函数值.
例:已知y=f(2x+1)的定义域为[1,2].
(1)求f(x)的定义域;
(2)求f(2x-1)的定义域.
解:(1)由于y=f(2x+1)的定义域为[1,2],
∴1≤x≤2,∴3≤2x+1≤5,
∴函数f(x)的定义域为[3,5].
(2)由(1)可知,3≤2x-1≤5,∴2≤x≤3,
∴函数f(2x-1)的定义域为[2,3].
①若f(x)是整式,则函数的定义域为R;
②若f(x)是分式,函数的分母不为零;
③偶次根式的被开方数非负;
④零的零次方没有意义;
⑤组合型函数的定义域是各个初等函数定义域的交集.
⑥当函数y=f(x)是用表格给出时,函数的定义域是指表格中实数的集合.
⑦当函数y=f(x)是用图象给出时,函数的定义域是指图象在x轴上投影所覆盖的实数的集合.
如何确定函数的定义域?
课堂小结
1.函数定义:
3.求函数定义域
(1)自然定义域:使函数解析式有意义的自变量的一切值;
(2)限定定义域:受某种条件制约或有附加条件的定义域应用问题、几何问题中的函数定义域,要考虑自变量的实际意义和几何意义.
2.函数的三要素:定义域、值域、对应关系.
作业布置:求下列函数的定义域:
作业布置:求下列函数的定义域:
故函数的定义域为
-2
1
2
定义域为
{5}.
x
{x|x
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
