2.2.1函数的概念 第2课时 课件(共20张PPT)
文档属性
| 名称 | 2.2.1函数的概念 第2课时 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 14:44:02 | ||
图片预览








文档简介
(共20张PPT)
数学北师大
必修1
2.2.1函数的概念第2课时
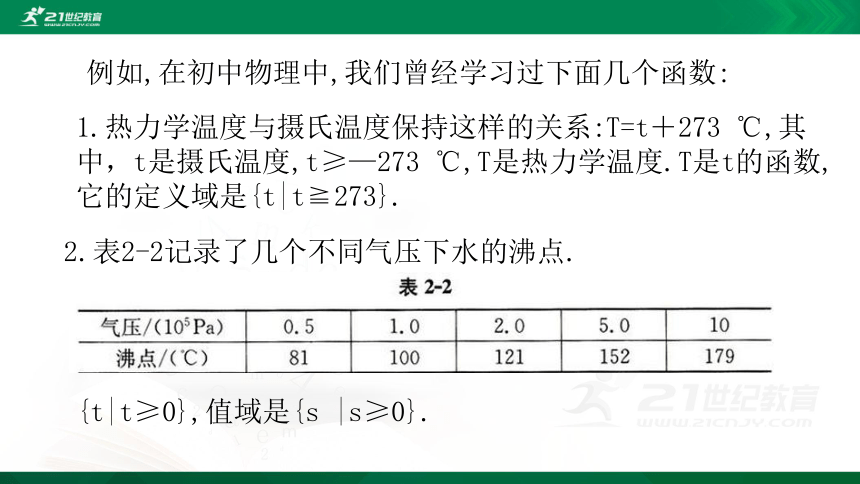
例如,在初中物理中,我们曾经学习过下面几个函数:
1.热力学温度与摄氏温度保持这样的关系:T=t+273
℃,其中,t是摄氏温度,t≥—273
℃,T是热力学温度.T是t的函数,它的定义域是{t|t≧273}.
2.表2-2记录了几个不同气压下水的沸点.
{t|t≥0},值域是{s
|s≥0}.
定义
名称
符号
数轴表示
a
b
a
b
a
b
a
b
{x︱a≤x≤b}
{x︱a{x︱a≤x{x︱a闭区间
开区间
[a,b]
(a,b)
[a,b)
(a,b]
这里实数a,b都叫作相应区间的端点.
半开半闭区间
半开半闭区间
区间
研究函数常常用到区间的概念.
设a,b是两个实数,而且a实数集R也可用区间表示为(一∞,+∞)
,
“∞”读作“无穷大”,
“—∞”读作“负无穷大”,“十∞”读作“正无穷大”.
我们还可以把满足x≥a,x
>a,x≤b,x,+∞),(-∞,b],(一∞,b).
集合
符号
数轴表示
R
{x︱x≥a}
{x︱x>a}
{x︱x
≤
b}
{x︱x
<
b}
a
a
b
b
做一做
(-∞,+
∞)
[a,+
∞)
(a,+
∞
)
(-
∞,b]
(-
∞,b)
(1)区间是集合;
(2)区间的左端点小于右端点;
(3)区间中的元素都是点,可以用数字表示;
(4)任何区间都可以在数轴上表示出来;
(5)以“-∞”,“+∞”为区间的一端时,这一端必须是小括号.
例如(-∞,100]
注意
例1某山海拔7500
m,海平面温度为25℃,气温是海拔高度的函数,而且高度每升高100
m,气温下降0.6
℃.请你用解析表达式表示出气温T随海拔高度x变化的函数关系,并指出函数的定义域和值域.
解函数解析式为
函数的定义域为[0,7500],值域为[一20,25].
探究2 只有当两个函数的定义域、值域,对应法则都相同时,两个函数才表示同一函数,但由于值域是由定义域和对应法则确定的,所以只要定义域及对应法则相同,两函数即表示同一函数.
两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关.
复合形式的求值问题,可以从里到外逐层求解.
探究3 计算f[f(x0)]的值的步骤:
(1)先求出f(x0)的值;
(2)然后把f(x0)的结果进一步代入函数的表达式中,即可得到f[f(x0)]的值.
例4.已知函数y=x2-4x-5,求:
(1)x∈R时的函数值域;
(2)x∈{-1,0,1,2,3,4}时的值域;
(3)x∈[-2,1]时的值域.
[分析] 函数值域是由定义域与对应关系所确定的,在求函数有关问题时,始终要把握好“定义域优先”的原则.
[解] (1)x∈R,y=x2-4x-5=(x-2)2-9,值域为[-9,+∞).
(2)当x=-1时,y=(-1)2-4×(-1)-5=0;
当x=0时,y=-5;
当x=1时,y=12-4×1-5
=-8;
当x=2时,y=22-4×2-5
=-9;
当x=3时,y=32-4×3-5
=-8;
当x=4时,y=42-4×4-5
=-5.
∴当x∈{-1,0,1,2,3,4}时函数y=x2-4x-5的值域为{0,-5,-8,-9}.
(3)∵y=x2-4x-5(x∈[-2,1])的图象如图1所示,由图象可知函数y=x2-4x-5在x∈[-2,1]上的最小值为f(1)=12-4×1-5=-8,最大值为f(-2)=(-2)2-4×(-2)-5=7.
∴其值域为[-8,7].
[点评] 1.求函数的值域应遵循“定义域优先”的原则.
2.求二次函数的值域要结合二次函数的图象求其值域.
1.函数的本质:两个非空数集间的一种确定的对应关系.由于函数的定义域和对应关系一经确定,值域随之确定,所以判断两个函数是否相等只须两个函数的定义域和对应关系一样即可.
2.f(x)是函数符号,f表示对应关系,f(x)表示x对应的函数值,绝对不能理解为f与x的乘积.在不同的函数中f的具体含义不同,由以上三个实例可看出对应关系可以是解析式、图象、表格等.函数除了可用符号f(x)表示外,还可用g(x),F(x)等表示.
知识小结
1.对于函数y=f(x),以下说法正确的有(
)
①y是x的函数
②对于不同的x,
y的值也不同
③
f(a)表示当x=a时函数f(x)的值,是一个常量
④
f(x)一定可以用一个具体的式子表示出来
A.1个
B.2个
C.3个
D.4个
B
作业布置:
2.给出四个命题中,正确有…………(
)
①函数就是定义域到值域的对应关系
②若函数的定义域只含有一个元素,则值域也只有一个元素
③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立
④定义域和对应关系确定后,函数值也就确定了
A.1个
B.2个
C.3个
D.4个
D
3.(2008
山东)设函数
则
的值为(
)
A.
B.
C.
D.18
A
解析:∵2>1
∴
=22+2-2=4,此时
=
∵
≤1
∴
=1-
=
教材习题答案
2.(1)f(2)=28;f(-2)=-28;f(2)+f(-2)=0
3.(1)不相等,因为前者的定义域为{t∣0≤t
≤26},而后者的定义域为R.
(2)不相等,因为前者的定义域为R,而后者的定义域为{x
∣x≠0}.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大
必修1
2.2.1函数的概念第2课时
例如,在初中物理中,我们曾经学习过下面几个函数:
1.热力学温度与摄氏温度保持这样的关系:T=t+273
℃,其中,t是摄氏温度,t≥—273
℃,T是热力学温度.T是t的函数,它的定义域是{t|t≧273}.
2.表2-2记录了几个不同气压下水的沸点.
{t|t≥0},值域是{s
|s≥0}.
定义
名称
符号
数轴表示
a
b
a
b
a
b
a
b
{x︱a≤x≤b}
{x︱a
开区间
[a,b]
(a,b)
[a,b)
(a,b]
这里实数a,b都叫作相应区间的端点.
半开半闭区间
半开半闭区间
区间
研究函数常常用到区间的概念.
设a,b是两个实数,而且a
,
“∞”读作“无穷大”,
“—∞”读作“负无穷大”,“十∞”读作“正无穷大”.
我们还可以把满足x≥a,x
>a,x≤b,x
集合
符号
数轴表示
R
{x︱x≥a}
{x︱x>a}
{x︱x
≤
b}
{x︱x
<
b}
a
a
b
b
做一做
(-∞,+
∞)
[a,+
∞)
(a,+
∞
)
(-
∞,b]
(-
∞,b)
(1)区间是集合;
(2)区间的左端点小于右端点;
(3)区间中的元素都是点,可以用数字表示;
(4)任何区间都可以在数轴上表示出来;
(5)以“-∞”,“+∞”为区间的一端时,这一端必须是小括号.
例如(-∞,100]
注意
例1某山海拔7500
m,海平面温度为25℃,气温是海拔高度的函数,而且高度每升高100
m,气温下降0.6
℃.请你用解析表达式表示出气温T随海拔高度x变化的函数关系,并指出函数的定义域和值域.
解函数解析式为
函数的定义域为[0,7500],值域为[一20,25].
探究2 只有当两个函数的定义域、值域,对应法则都相同时,两个函数才表示同一函数,但由于值域是由定义域和对应法则确定的,所以只要定义域及对应法则相同,两函数即表示同一函数.
两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关.
复合形式的求值问题,可以从里到外逐层求解.
探究3 计算f[f(x0)]的值的步骤:
(1)先求出f(x0)的值;
(2)然后把f(x0)的结果进一步代入函数的表达式中,即可得到f[f(x0)]的值.
例4.已知函数y=x2-4x-5,求:
(1)x∈R时的函数值域;
(2)x∈{-1,0,1,2,3,4}时的值域;
(3)x∈[-2,1]时的值域.
[分析] 函数值域是由定义域与对应关系所确定的,在求函数有关问题时,始终要把握好“定义域优先”的原则.
[解] (1)x∈R,y=x2-4x-5=(x-2)2-9,值域为[-9,+∞).
(2)当x=-1时,y=(-1)2-4×(-1)-5=0;
当x=0时,y=-5;
当x=1时,y=12-4×1-5
=-8;
当x=2时,y=22-4×2-5
=-9;
当x=3时,y=32-4×3-5
=-8;
当x=4时,y=42-4×4-5
=-5.
∴当x∈{-1,0,1,2,3,4}时函数y=x2-4x-5的值域为{0,-5,-8,-9}.
(3)∵y=x2-4x-5(x∈[-2,1])的图象如图1所示,由图象可知函数y=x2-4x-5在x∈[-2,1]上的最小值为f(1)=12-4×1-5=-8,最大值为f(-2)=(-2)2-4×(-2)-5=7.
∴其值域为[-8,7].
[点评] 1.求函数的值域应遵循“定义域优先”的原则.
2.求二次函数的值域要结合二次函数的图象求其值域.
1.函数的本质:两个非空数集间的一种确定的对应关系.由于函数的定义域和对应关系一经确定,值域随之确定,所以判断两个函数是否相等只须两个函数的定义域和对应关系一样即可.
2.f(x)是函数符号,f表示对应关系,f(x)表示x对应的函数值,绝对不能理解为f与x的乘积.在不同的函数中f的具体含义不同,由以上三个实例可看出对应关系可以是解析式、图象、表格等.函数除了可用符号f(x)表示外,还可用g(x),F(x)等表示.
知识小结
1.对于函数y=f(x),以下说法正确的有(
)
①y是x的函数
②对于不同的x,
y的值也不同
③
f(a)表示当x=a时函数f(x)的值,是一个常量
④
f(x)一定可以用一个具体的式子表示出来
A.1个
B.2个
C.3个
D.4个
B
作业布置:
2.给出四个命题中,正确有…………(
)
①函数就是定义域到值域的对应关系
②若函数的定义域只含有一个元素,则值域也只有一个元素
③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立
④定义域和对应关系确定后,函数值也就确定了
A.1个
B.2个
C.3个
D.4个
D
3.(2008
山东)设函数
则
的值为(
)
A.
B.
C.
D.18
A
解析:∵2>1
∴
=22+2-2=4,此时
=
∵
≤1
∴
=1-
=
教材习题答案
2.(1)f(2)=28;f(-2)=-28;f(2)+f(-2)=0
3.(1)不相等,因为前者的定义域为{t∣0≤t
≤26},而后者的定义域为R.
(2)不相等,因为前者的定义域为R,而后者的定义域为{x
∣x≠0}.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
