2.2.2 函数的表示法 第2课时 课件(共15张PPT)
文档属性
| 名称 | 2.2.2 函数的表示法 第2课时 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 14:49:25 | ||
图片预览





文档简介
(共15张PPT)
数学北师大
必修1
2.2.2
函数的表示法第2课时
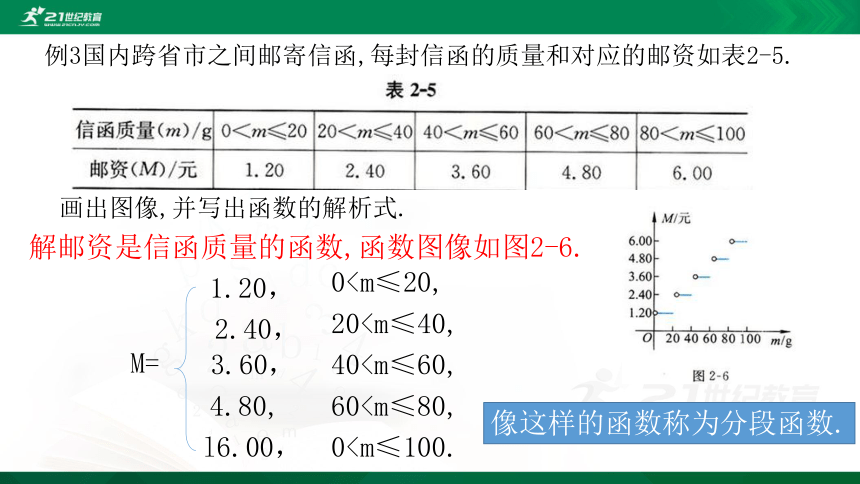
例3国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如表2-5.
画出图像,并写出函数的解析式.
解邮资是信函质量的函数,函数图像如图2-6.
0像这样的函数称为分段函数.
1.20,
02.40,
20M=
3.60,
404.80,
60l6.00,
所谓“分段函数”,习惯上指在定义域内的不同区间上,有不同的对应法则的函数。对它应有以下基本认识:
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值
域是各段值域的并集。
(3)分段函数的作图就是将分段函数在各段上的图象逐段作出,注意端点处的取舍情况。
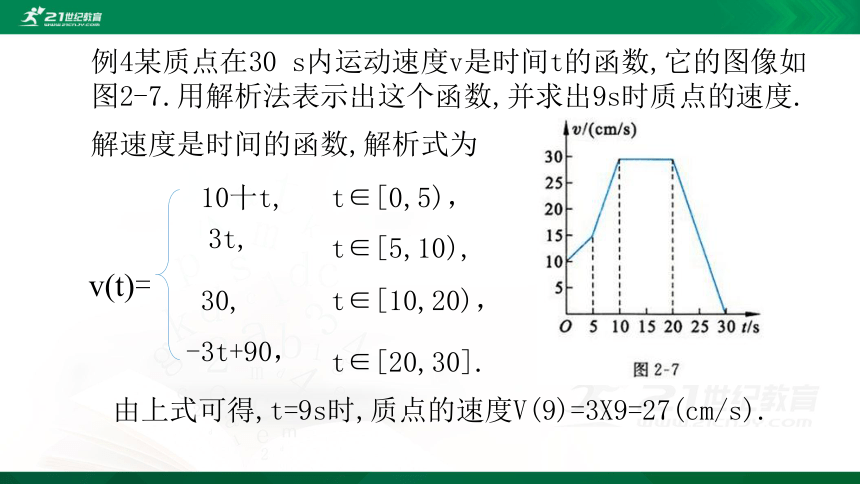
例4某质点在30
s内运动速度v是时间t的函数,它的图像如图2-7.用解析法表示出这个函数,并求出9s时质点的速度.
由上式可得,t=9s时,质点的速度V(9)=3X9=27(cm/s).
解速度是时间的函数,解析式为
10十t,
t∈[0,5),
3t,
t∈[5,10),
v(t)=
30,
t∈[10,20),
-3t+90,
t∈[20,30].
在实际问题中,要有针对性地选择适当的函数表示方法,
有时需要多种方法综合运用;
有时也需要把函数的某种表示方法转化为另一种表示方法.
例5
(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,则f(x)=________.
解:(1)设f(x)=ax+b(a≠0),
则3f(x+1)-2f(x-1)
=3ax+3a+3b-2ax+2a-2b
=ax+5a+b,
即ax+5a+b=2x+17不论x为何值都成立,
∴f(x)=2x+7.
采用待定系数法,
1.用配凑法或换元法求函数的解析式
求出来的式子要注明定义域
课堂小结
2.采用待定系数法
分段函数
1.已知f(x)是一次函数,且f(f(x))=4x+3,求f(x).
【分析】本题关键是设出一次函数的解析式,代入已知关系式,利用待定系数法求解.
【解析】设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=4x+3,
∴
解得
或
故所求的函数为f(x)=2x+1或f(x)=-2x-3.
作业布置
2.已知f(x)是二次函数且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式.
3.
已知f(x2+2)=x4+4x2,求f(x)的解析式.
错解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
设t=x2+2,则f(t)=t2-4,∴f(x)=x2-4.
错因分析:本题错解的原因是忽略了函数f(x)的定义域.上面的解法,似乎是无懈可击,然而从其结论,即f(x)=x2-4来看,并未注明f(x)的定义域,那么按一般理解,就应认为其定义域是全体实数.但是f(x)=x2-4的定义域不是全体实数.
3.
已知f(x2+2)=x4+4x2,求f(x)的解析式.
正解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
令t=x2+2(t≥2),则f(t)=t2-4(t≥2),
∴f(x)=x2-4(x≥2).
纠错心得:采用换元法求函数的解析式时,一定要注意换元后的自变量的取值范围.如本题中令t=x2+2后,则t≥2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大
必修1
2.2.2
函数的表示法第2课时
例3国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如表2-5.
画出图像,并写出函数的解析式.
解邮资是信函质量的函数,函数图像如图2-6.
0
1.20,
0
20
3.60,
40
60
所谓“分段函数”,习惯上指在定义域内的不同区间上,有不同的对应法则的函数。对它应有以下基本认识:
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值
域是各段值域的并集。
(3)分段函数的作图就是将分段函数在各段上的图象逐段作出,注意端点处的取舍情况。
例4某质点在30
s内运动速度v是时间t的函数,它的图像如图2-7.用解析法表示出这个函数,并求出9s时质点的速度.
由上式可得,t=9s时,质点的速度V(9)=3X9=27(cm/s).
解速度是时间的函数,解析式为
10十t,
t∈[0,5),
3t,
t∈[5,10),
v(t)=
30,
t∈[10,20),
-3t+90,
t∈[20,30].
在实际问题中,要有针对性地选择适当的函数表示方法,
有时需要多种方法综合运用;
有时也需要把函数的某种表示方法转化为另一种表示方法.
例5
(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,则f(x)=________.
解:(1)设f(x)=ax+b(a≠0),
则3f(x+1)-2f(x-1)
=3ax+3a+3b-2ax+2a-2b
=ax+5a+b,
即ax+5a+b=2x+17不论x为何值都成立,
∴f(x)=2x+7.
采用待定系数法,
1.用配凑法或换元法求函数的解析式
求出来的式子要注明定义域
课堂小结
2.采用待定系数法
分段函数
1.已知f(x)是一次函数,且f(f(x))=4x+3,求f(x).
【分析】本题关键是设出一次函数的解析式,代入已知关系式,利用待定系数法求解.
【解析】设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=4x+3,
∴
解得
或
故所求的函数为f(x)=2x+1或f(x)=-2x-3.
作业布置
2.已知f(x)是二次函数且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式.
3.
已知f(x2+2)=x4+4x2,求f(x)的解析式.
错解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
设t=x2+2,则f(t)=t2-4,∴f(x)=x2-4.
错因分析:本题错解的原因是忽略了函数f(x)的定义域.上面的解法,似乎是无懈可击,然而从其结论,即f(x)=x2-4来看,并未注明f(x)的定义域,那么按一般理解,就应认为其定义域是全体实数.但是f(x)=x2-4的定义域不是全体实数.
3.
已知f(x2+2)=x4+4x2,求f(x)的解析式.
正解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
令t=x2+2(t≥2),则f(t)=t2-4(t≥2),
∴f(x)=x2-4(x≥2).
纠错心得:采用换元法求函数的解析式时,一定要注意换元后的自变量的取值范围.如本题中令t=x2+2后,则t≥2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
