2.3 函数的单调性 课件(共29张PPT)
文档属性
| 名称 | 2.3 函数的单调性 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 14:58:24 | ||
图片预览





文档简介
(共29张PPT)
数学北师大
必修1
2.3
函数的单调性
在研究函数的过程中,我们最关心的是:当自变量变化时,函数值随着自变量的变化会如何变化.
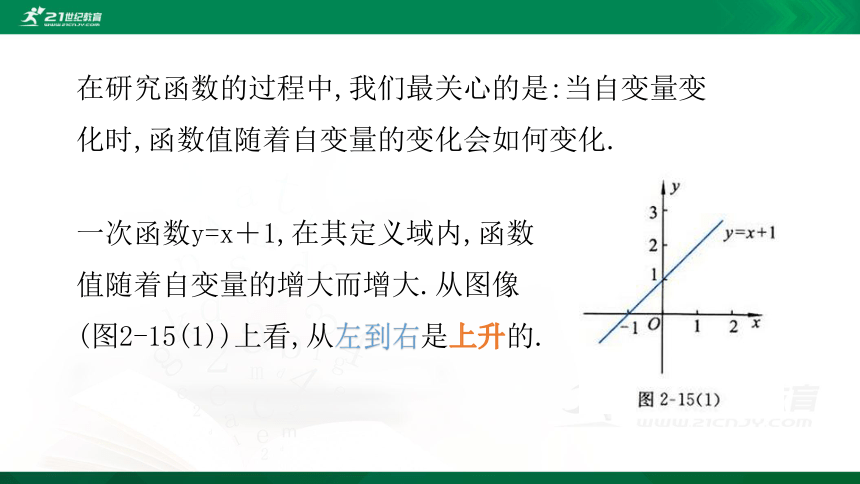
一次函数y=x+1,在其定义域内,函数值随着自变量的增大而增大.从图像(图2-15(1))上看,从左到右是上升的.
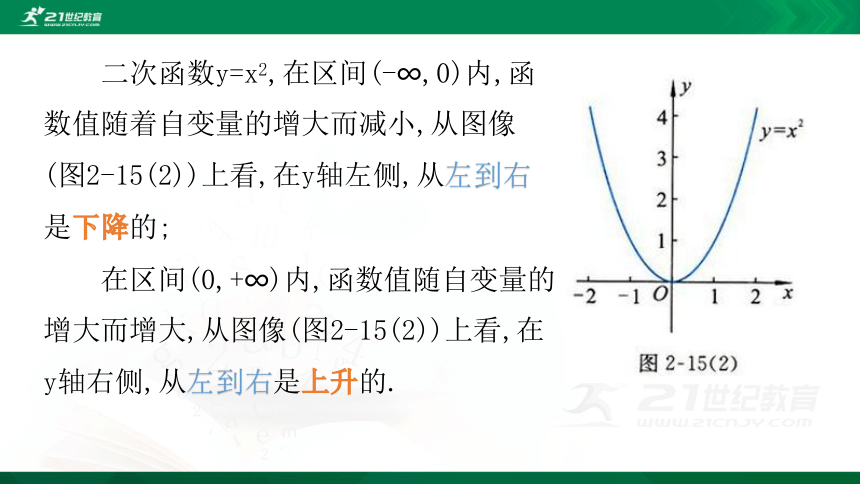
二次函数y=x2,在区间(-∞,0)内,函数值随着自变量的增大而减小,从图像(图2-15(2))上看,在y轴左侧,从左到右是下降的;
在区间(0,+∞)内,函数值随自变量的增大而增大,从图像(图2-15(2))上看,在y轴右侧,从左到右是上升的.
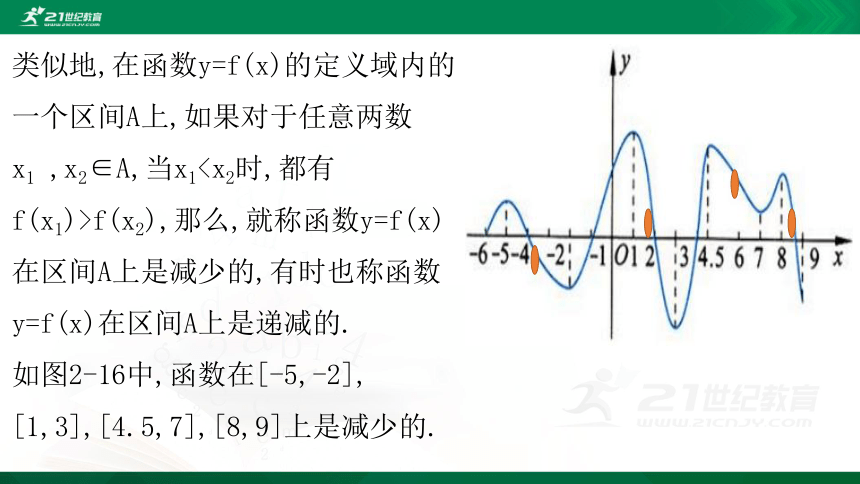
在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1
,x2∈A,当x1如图2-16中,函数在[一6,-5],[-2,1],[3,4.5],[7,8]上是增加的.
图2-16
单调区间之间必须用“,”隔开,或者用“和”
连接,但千万不能用“∪”连接,也不能用“或”,
“且”连接。
类似地,在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1
,x2∈A,当x1f(x2),那么,就称函数y=f(x)在区间A上是减少的,有时也称函数y=f(x)在区间A上是递减的.
如图2-16中,函数在[-5,-2],
[1,3],[4.5,7],[8,9]上是减少的.
如果y=f(x)在区间A上是增加的或是减少的,那么称A为单调区间.在单调区间上,如果函数是增加的,那么它的图像是上升的;
如果函数是减少的,那么它的图像是下降的.
一般地,对于函数y=f(x)的定义域内的一个子集A,如果对于任意两数x1
,x2
∈A,当x1称这个函数为增函数。
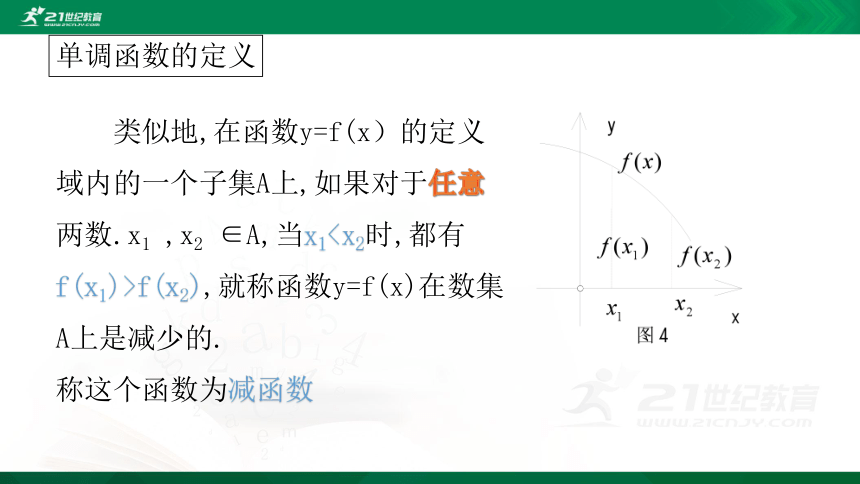
单调函数的定义
类似地,在函数y=f(x)的定义域内的一个子集A上,如果对于任意两数.x1
,x2
∈A,当x1f(x2),就称函数y=f(x)在数集A上是减少的.
称这个函数为减函数
单调函数的定义
当x1x2时,都有f(x1)>f(x2)
函数y=f(x)在数集A上是增加的
当x1f(x2),x1>x2时,都有f(x1)对于任意两数.x1
,x2
∈A,
定义域与值域的大小,异号(一个大于号,另一个小于号)减少
定义域与值域的大小,同号(都是大于号或小于号)增加,
定义域与值域的大小,同号(都是大于号或小于号)增加,
异号(一个大于号,另一个小于号)减少
如果函数y=f(x)在定义域的某个子集上是增加的或是减少的,那么就称函数y=f(x)在这个子集上具有单调性.
单调性
如果函数y=f(x)在整个定义域内是增加的或是减少的,我们分别称这个函数为增函数或减函数,统称为单调函数.
注意:
①
函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
②必须是对于区间D内的任意两个自变量x1,x2;当x1.
注意:函数的单调性是对某个区间而言的,对于单独的一点,由于它的函数值是唯一确定的常数,因而没有增减变化,所以不存在单调性问题;对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此,在考虑它的单调区间时,包括不包括端点都可以;
例1说出函数f(x)=
的单调区间,并指明在该区间上的单调性.
解(一∞,0)和(0,
+∞)都是函数的单调区间,在这两个区间上函数f(x)=
是减少的.
例2画出函数f(x)=3x+2的图像,判断它的单调性,并加以证明.
解作出f(x)=3x+2的图像(如图).
由图看出,函数f(x)的图像在R上是上升的,函数f(x)是R上的增函数.
下面进行证明:任取x1,x2∈R,且x1,
则x1一x2<0.
所以f(x1)-
f(x2)=(3x1+2)-
(3x2+2)=3(x1一x2)<0,
即f(x1)由单调函数的定义可知,函数f(x)=3x+2是R上的增函数.
判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
①
任取x1,x2∈D,且x1②
作差f(x1)-f(x2);
③
变形(通常是因式分解和配方);
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性).
我们观察图2-16,可以看出对于定义域中的任意x
,都有f(x)≤f(1),
我们就说f(1)是这个函数的最大值.
一般地,对于函数y=f(x),其定义域为D,如果存在x0∈D,f(x0)=M,使得对于任意的x∈D,都有f(x)≤M,那么,我们称M是函数y=
f(x)的最大值,
即当x=x0时,f(x0)是函数y=f(x)的最大值,记作ymax=
f(x0).
函数y=f(x)的最大值定义
类似:一般地,对于函数y=f(x),其定义域为D,如果存在x0∈D,f(x0)=M,使得对于任意的x∈D,都有f(x)≧M,那么,我们称M是函数y=
f(x)的最小值,
即当x=x0时,f(x0)是函数y=f(x)的最小值,记作ymax=
f(x0).
例3如图2-18,某地要修一个圆形的喷水池,水流在各个方向上以相同的抛物线路径落下,以水池的中央为坐标原点,水平方向为x轴、竖直方向为y轴建立平面直角坐标系,那么水流喷出的高度h(单位:m)与水平
距离x(单位:m)之间的函数关系式为h=-x2+2x+1.25
x∈[0,2.5
]求水流喷出的高度h的最大值是多少?
解由函数h=-x2+2x+1.25,x∈[0,2.5]的图像可知,
显然,函数图像的顶点就是水流喷出的最高点.此时函数取得最大值.
对于函数h=-x2
+2x+2.5,x∈[0,2.5],当x=1时,函数有最大值
hmax=-12+2×1+1.25=2.25(m).于是水流喷出的最高高度是2.25m.
例4已知函数
f(x)=-
x∈[0,2],求函数的最大值和最小值.
函数f(x)在区间[0,2]上递增,所以,函数f(x)在区间[0,2]的两个端点上分别取得最小值和最大值.
解设x1,x2
是区间[0,2]上的任意两个实数,且x1f(x1)-
f(x2)=
-
-(-
)
分析由函数f(x)=-
x∈[0,2]的图像可知,
由0≤x10,(x1+1)(x2+1)>0,
所以f(x1)-f(x2)<0,即f(x1)右端点取得最大值,
因此,函数f(x)=-
在区间[0,2]的左端点取得最小值,
即最小值是f(0)=-2,最大值是f(2)=
课堂小结:
单调函数的定义
增函数。
减函数
单调性
增函数或减函数,统称为单调函数.
1.若f(x)=
x2+bx+c
且f(1)=0,f(3)=0.
试证明函数f(x)在区间(2,+)上是增函数。
作业布置:
2.已知f(x)是定义在[-1,1]上的增函数,且f(x-1)<f(1-3x),求x的取值范围.
注意:(1)在给定的区间内,当某个代数式的符号无法确定时(如本题中x1x2-a),可取极端情况(如x1=x2)入手分析,以此为界分类讨论.
4.
已知函数y=f(x)的定义域是[a,b],a【证明】因为当x∈[a,c]时,f(x)是增函数,
所以对于任意x∈[a,c],都有f(x)≤f(c).
又因为当x∈[c,b]时,f(x)是减函数,
所以对于任意x∈[c,b],都有f(x)≤f(c).
因此对于任意x∈[a,b],都有f(x)≤f(c),即f(x)在x=c时取得最大值.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大
必修1
2.3
函数的单调性
在研究函数的过程中,我们最关心的是:当自变量变化时,函数值随着自变量的变化会如何变化.
一次函数y=x+1,在其定义域内,函数值随着自变量的增大而增大.从图像(图2-15(1))上看,从左到右是上升的.
二次函数y=x2,在区间(-∞,0)内,函数值随着自变量的增大而减小,从图像(图2-15(2))上看,在y轴左侧,从左到右是下降的;
在区间(0,+∞)内,函数值随自变量的增大而增大,从图像(图2-15(2))上看,在y轴右侧,从左到右是上升的.
在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1
,x2∈A,当x1
图2-16
单调区间之间必须用“,”隔开,或者用“和”
连接,但千万不能用“∪”连接,也不能用“或”,
“且”连接。
类似地,在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1
,x2∈A,当x1
如图2-16中,函数在[-5,-2],
[1,3],[4.5,7],[8,9]上是减少的.
如果y=f(x)在区间A上是增加的或是减少的,那么称A为单调区间.在单调区间上,如果函数是增加的,那么它的图像是上升的;
如果函数是减少的,那么它的图像是下降的.
一般地,对于函数y=f(x)的定义域内的一个子集A,如果对于任意两数x1
,x2
∈A,当x1
单调函数的定义
类似地,在函数y=f(x)的定义域内的一个子集A上,如果对于任意两数.x1
,x2
∈A,当x1
称这个函数为减函数
单调函数的定义
当x1
函数y=f(x)在数集A上是增加的
当x1
,x2
∈A,
定义域与值域的大小,异号(一个大于号,另一个小于号)减少
定义域与值域的大小,同号(都是大于号或小于号)增加,
定义域与值域的大小,同号(都是大于号或小于号)增加,
异号(一个大于号,另一个小于号)减少
如果函数y=f(x)在定义域的某个子集上是增加的或是减少的,那么就称函数y=f(x)在这个子集上具有单调性.
单调性
如果函数y=f(x)在整个定义域内是增加的或是减少的,我们分别称这个函数为增函数或减函数,统称为单调函数.
注意:
①
函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
②必须是对于区间D内的任意两个自变量x1,x2;当x1
注意:函数的单调性是对某个区间而言的,对于单独的一点,由于它的函数值是唯一确定的常数,因而没有增减变化,所以不存在单调性问题;对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此,在考虑它的单调区间时,包括不包括端点都可以;
例1说出函数f(x)=
的单调区间,并指明在该区间上的单调性.
解(一∞,0)和(0,
+∞)都是函数的单调区间,在这两个区间上函数f(x)=
是减少的.
例2画出函数f(x)=3x+2的图像,判断它的单调性,并加以证明.
解作出f(x)=3x+2的图像(如图).
由图看出,函数f(x)的图像在R上是上升的,函数f(x)是R上的增函数.
下面进行证明:任取x1,x2∈R,且x1
则x1一x2<0.
所以f(x1)-
f(x2)=(3x1+2)-
(3x2+2)=3(x1一x2)<0,
即f(x1)
判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
①
任取x1,x2∈D,且x1
作差f(x1)-f(x2);
③
变形(通常是因式分解和配方);
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性).
我们观察图2-16,可以看出对于定义域中的任意x
,都有f(x)≤f(1),
我们就说f(1)是这个函数的最大值.
一般地,对于函数y=f(x),其定义域为D,如果存在x0∈D,f(x0)=M,使得对于任意的x∈D,都有f(x)≤M,那么,我们称M是函数y=
f(x)的最大值,
即当x=x0时,f(x0)是函数y=f(x)的最大值,记作ymax=
f(x0).
函数y=f(x)的最大值定义
类似:一般地,对于函数y=f(x),其定义域为D,如果存在x0∈D,f(x0)=M,使得对于任意的x∈D,都有f(x)≧M,那么,我们称M是函数y=
f(x)的最小值,
即当x=x0时,f(x0)是函数y=f(x)的最小值,记作ymax=
f(x0).
例3如图2-18,某地要修一个圆形的喷水池,水流在各个方向上以相同的抛物线路径落下,以水池的中央为坐标原点,水平方向为x轴、竖直方向为y轴建立平面直角坐标系,那么水流喷出的高度h(单位:m)与水平
距离x(单位:m)之间的函数关系式为h=-x2+2x+1.25
x∈[0,2.5
]求水流喷出的高度h的最大值是多少?
解由函数h=-x2+2x+1.25,x∈[0,2.5]的图像可知,
显然,函数图像的顶点就是水流喷出的最高点.此时函数取得最大值.
对于函数h=-x2
+2x+2.5,x∈[0,2.5],当x=1时,函数有最大值
hmax=-12+2×1+1.25=2.25(m).于是水流喷出的最高高度是2.25m.
例4已知函数
f(x)=-
x∈[0,2],求函数的最大值和最小值.
函数f(x)在区间[0,2]上递增,所以,函数f(x)在区间[0,2]的两个端点上分别取得最小值和最大值.
解设x1,x2
是区间[0,2]上的任意两个实数,且x1
f(x2)=
-
-(-
)
分析由函数f(x)=-
x∈[0,2]的图像可知,
由0≤x1
所以f(x1)-f(x2)<0,即f(x1)
因此,函数f(x)=-
在区间[0,2]的左端点取得最小值,
即最小值是f(0)=-2,最大值是f(2)=
课堂小结:
单调函数的定义
增函数。
减函数
单调性
增函数或减函数,统称为单调函数.
1.若f(x)=
x2+bx+c
且f(1)=0,f(3)=0.
试证明函数f(x)在区间(2,+)上是增函数。
作业布置:
2.已知f(x)是定义在[-1,1]上的增函数,且f(x-1)<f(1-3x),求x的取值范围.
注意:(1)在给定的区间内,当某个代数式的符号无法确定时(如本题中x1x2-a),可取极端情况(如x1=x2)入手分析,以此为界分类讨论.
4.
已知函数y=f(x)的定义域是[a,b],a
所以对于任意x∈[a,c],都有f(x)≤f(c).
又因为当x∈[c,b]时,f(x)是减函数,
所以对于任意x∈[c,b],都有f(x)≤f(c).
因此对于任意x∈[a,b],都有f(x)≤f(c),即f(x)在x=c时取得最大值.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
